- •Розділ II. Елементи аналітичної геометрії
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •Питання для повторення
- •1) Підставимо в канонічне рівняння еліпса 4078 замість такоординати точкиА, а також дане значення . Одержимо рівняння:.
- •Задачі для самостійної роботи
- •Питання для повторення
- •Задачі для самостійної роботи
- •§ 48. Розв’язування задач на складання рівнянь поверхонь та їх дослідження
- •Задачі для самостійної роботи
- •Питання для повторення
- •Відповіді
- •Додаток
- •Програма модульного контролю з теми
- •Лінійна і векторна алгебра
- •Теоретичні запитання.
- •Зразки практичних завданнь.
- •Програма модульного контролю з теми аналітична геометрія Теоретичні запитання.
- •Зразки практичних завдань.
- •Література.
Задачі для самостійної роботи
Привести до канонічного вигляду рівняння кривих другого порядку:
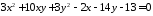 ;
;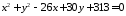 ;
;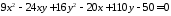 ;
;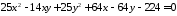 ;
;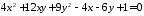 ;
;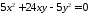 ;
;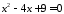 ;
;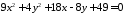 ;
;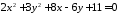 ;
;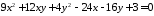 .
.
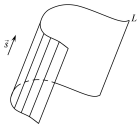
10545Equation Section (Next)§ 45. Циліндричні поверхні. Рівняння еліптичного або кругового циліндру
Нехай
у просторі є деяка плоска лінія
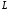 і заданий ненульовий вектор
і заданий ненульовий вектор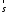 .
.
Поверхня,
утворена прямими, що проходять через
кожну точку лінії
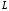 паралельно до заданого вектора
паралельно до заданого вектора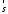 ,
називаєтьсяциліндричною
поверхнею
(Рис. 45.1).
,
називаєтьсяциліндричною
поверхнею
(Рис. 45.1).
Прямі,
що утворюють циліндричну поверхню,
називаються твірними,
а лінія
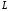 називаєтьсянапрямною.
називаєтьсянапрямною.
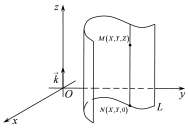
Складемо
рівняння циліндричної поверхні за умов,
що напрямною є крива, що міститься у
площині
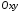 ,
а вектор
,
а вектор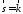 - орту осі
- орту осі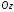 .
.
Тоді напрямна задається рівнянням
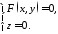 10645106\* MERGEFORMAT (.)
10645106\* MERGEFORMAT (.)
а
твірні паралельні осі
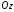 (Рис. 45.2).
(Рис. 45.2).
|
|
|
|
Рис. 45.1 |
Рис. 45.2 |
Візьмемо
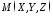 - довільну точку циліндричної поверхні.
Проведемо через цю точку твірну до
перетину з напрямною у точці
- довільну точку циліндричної поверхні.
Проведемо через цю точку твірну до
перетину з напрямною у точці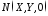 .
Оскільки ця точка належить до напрямної,
то її координати мають задовольняти
рівняння 45106. Отже, для будь якої точки
на циліндрі координати
.
Оскільки ця точка належить до напрямної,
то її координати мають задовольняти
рівняння 45106. Отже, для будь якої точки
на циліндрі координати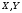 задовольняють першому рівнянню системи
45106, а третя координата
задовольняють першому рівнянню системи
45106, а третя координата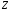 може бути довільною:
може бути довільною:
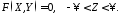 10745107\* MERGEFORMAT (.)
10745107\* MERGEFORMAT (.)
Рівняння 45107 і є рівнянням циліндричної поверхні, що зображена на Рис. 45.2.
Якщо у якості напрямної взяти еліпс, то з 45107 отримаємо рівняння еліптичного циліндра:
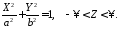 10845108\* MERGEFORMAT (.)
10845108\* MERGEFORMAT (.)
Якщо
 ,
то еліпс є колом і з 45108 знаходимо
рівняння кругового циліндра:
,
то еліпс є колом і з 45108 знаходимо
рівняння кругового циліндра:
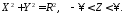 10945109\* MERGEFORMAT (.)
10945109\* MERGEFORMAT (.)
11046Equation Section (Next)§ 46. Конічні поверхні. Рівняння кругового конуса
Нехай
задана плоска лінія
 і точка
і точка ,
що не знаходиться з цією лінією у одній
площині. Поверхня, яка утворюється
прямими, що проходять через кожну точку
заданої лінії
,
що не знаходиться з цією лінією у одній
площині. Поверхня, яка утворюється
прямими, що проходять через кожну точку
заданої лінії і задану точку
і задану точку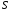 ,
називаєтьсяконічною
поверхнею,
або конусом
(Рис. 46.1). Лінія
,
називаєтьсяконічною
поверхнею,
або конусом
(Рис. 46.1). Лінія
 - називається напрямною конуса, точка
- називається напрямною конуса, точка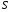 - вершиною конуса, а лінії, що проходять
через точку напрямної і вершину,
називаються твірними.
- вершиною конуса, а лінії, що проходять
через точку напрямної і вершину,
називаються твірними.
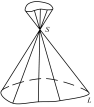
Рис. 46.1
Візьмемо
у якості напрямної коло радіуса
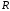 ,
що знаходиться у площині
,
що знаходиться у площині з центром в точці
з центром в точці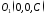 на
осі
на
осі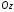 (Рис.46.2).
(Рис.46.2).

Рис. 46.2
Таке
коло у системі
 визначається
системою рівнянь
визначається
системою рівнянь
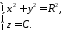 11146111\* MERGEFORMAT (.)
11146111\* MERGEFORMAT (.)
Припускаємо,
що точка
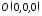 -
вершина конуса. Нехай
-
вершина конуса. Нехай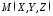 -
довільна точка на конусі. Проведемо
твірну
-
довільна точка на конусі. Проведемо
твірну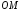 ,
яка перетне коло 46111, що є напрямним, у
точці
,
яка перетне коло 46111, що є напрямним, у
точці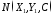 .
Оскільки точка
.
Оскільки точка належить до кола, то її координати
задовольняють 46111, зокрема виконується
рівність:
належить до кола, то її координати
задовольняють 46111, зокрема виконується
рівність:
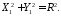 11246112\* MERGEFORMAT (.)
11246112\* MERGEFORMAT (.)
Вектори
 і
і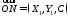 - колінеарні, тому
- колінеарні, тому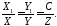
З
останньої рівності знаходимо
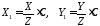 і підставляємо у 46112:
і підставляємо у 46112:
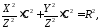
або
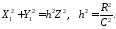 11346113\* MERGEFORMAT (.)
11346113\* MERGEFORMAT (.)
Останнє рівняння і визначає розглянутий конус.
11447Equation Section (Next)§ 47. Поверхні обертання. Поверхні обертання другого порядку
Поверхнею обертання називається поверхня, утворена обертанням плоскої лінії навколо прямої, що знаходиться у тій же самій площині. Пряма, навколо якої відбувається обертання, називається віссю обертання.

Рис. 47.1
Розглянемо
криву
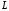 ,
яка в системі координат
,
яка в системі координат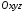 знаходиться у площині
знаходиться у площині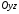 і задається рівнянням
і задається рівнянням
 11547115\* MERGEFORMAT (.)
11547115\* MERGEFORMAT (.)
Знайдемо
рівняння поверхні, що утворюється
обертанням цієї кривої навколо осі
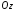 (Рис.47.1).
Розглянемо довільну точку поверхні
(Рис.47.1).
Розглянемо довільну точку поверхні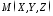 .
Через цю точку проведемо площину,
перпендикулярну до осі
.
Через цю точку проведемо площину,
перпендикулярну до осі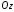 .
Нехай
.
Нехай -
точка перетину цієї площини з віссю
-
точка перетину цієї площини з віссю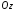 ,
а
,
а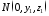 -
точка перетину з кривою
-
точка перетину з кривою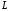 .
Тоді
.
Тоді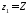 ,
а
,
а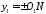 .
Але
.
Але
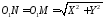 ,
як радіуси одного кола. Отже, координати
точки
,
як радіуси одного кола. Отже, координати
точки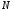 дорівнюють
дорівнюють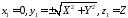 і оскільки точка
і оскільки точка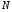 належить кривій
належить кривій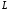 ,
то мають задовольняти рівняння 47115:
,
то мають задовольняти рівняння 47115:
 11647116\* MERGEFORMAT (.)
11647116\* MERGEFORMAT (.)
Таким
чином, 47116
є рівнянням розглянутої поверхні
обертання. Аналогічно отримується
рівняння поверхні, що утворюється
обертанням кривої 47115 навколо осі

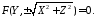 11747117\* MERGEFORMAT (.)
11747117\* MERGEFORMAT (.)
Коли
лінія знаходиться у площині
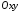 і її рівняння
і її рівняння
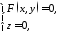
то
рівняння поверхні, утвореної обертанням
цієї лінії навколо осі
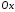 має вигляд:
має вигляд:
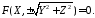 11847118\* MERGEFORMAT (.)
11847118\* MERGEFORMAT (.)
Розглянемо поверхні, що утворюються при обертанні кривих другого порядку, заданих канонічними рівняннями.
Еліпсоїд обертання.
Нехай
еліпс, що знаходиться у площині
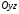 ,
задається рівнянням
,
задається рівнянням
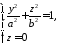
і
обертається навколо осі
 (Рис. 47.2)
(Рис. 47.2)

Рис. 47.2
Утворена при цьому поверхня називається еліпсоїдом обертання і має рівняння (див.47116)
 11947119\* MERGEFORMAT (.)
11947119\* MERGEFORMAT (.)
Однопорожнинний гіперболоїд обертання
Візьмемо
у площині
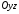 гіперболу
гіперболу
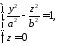
і
здійснимо її обертання навколо осі
 (Рис. 47.3)
(Рис. 47.3)
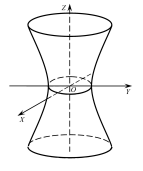
Рис. 47.3
Утворена при цьому поверхня називається однопорожнинним гіперболоїдом обертання і має рівняння
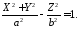 12047120\* MERGEFORMAT (.)
12047120\* MERGEFORMAT (.)
Двопорожнинний гіперболоїд обертання
Якщо
цю саму гіперболу обертати навколо осі
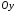 ,
то отримаємо поверхню, яка називаєтьсядвопорожнинним
гіперболоїдом обертання
(Рис. 47.4) і згідно з 47117 визначається
рівнянням
,
то отримаємо поверхню, яка називаєтьсядвопорожнинним
гіперболоїдом обертання
(Рис. 47.4) і згідно з 47117 визначається
рівнянням
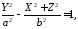 або
або
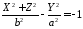 12147121\* MERGEFORMAT (.)
12147121\* MERGEFORMAT (.)
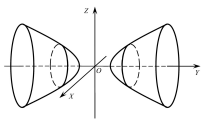
Рис. 47.4
Параболоїд обертання.
Нехай парабола
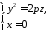
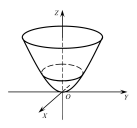
Рис. 47.5
обертається
навколо осі
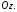 (Рис. 47.5). Утворена поверхня називаєтьсяпараболоїдом
обертання
і визначається рівнянням
(Рис. 47.5). Утворена поверхня називаєтьсяпараболоїдом
обертання
і визначається рівнянням
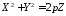 12247122\* MERGEFORMAT (.)
12247122\* MERGEFORMAT (.)