10.4. Графические решения прямых позиционных задач на пересечение
10.4.1. Решение прямой задачи №1 (на определение взаимного располо-жения двух плоскостей по их двухкар-тинному комплексному чертежу)
Известно, что две плоскости могут совпадать или пересекаться ( в том чис-ле под углами 0 и 90). При этом каж-дая из них может занимать в простран-стве как частные, так и общее положе-ние.
Так как задача является прямой, то её непосредственному графическому решению должен предшествовать сис-темный анализ её возможных условий, определяемых особенностями положе-ния каждой из плоскостей по отноше-нию к плоскостям проекций.
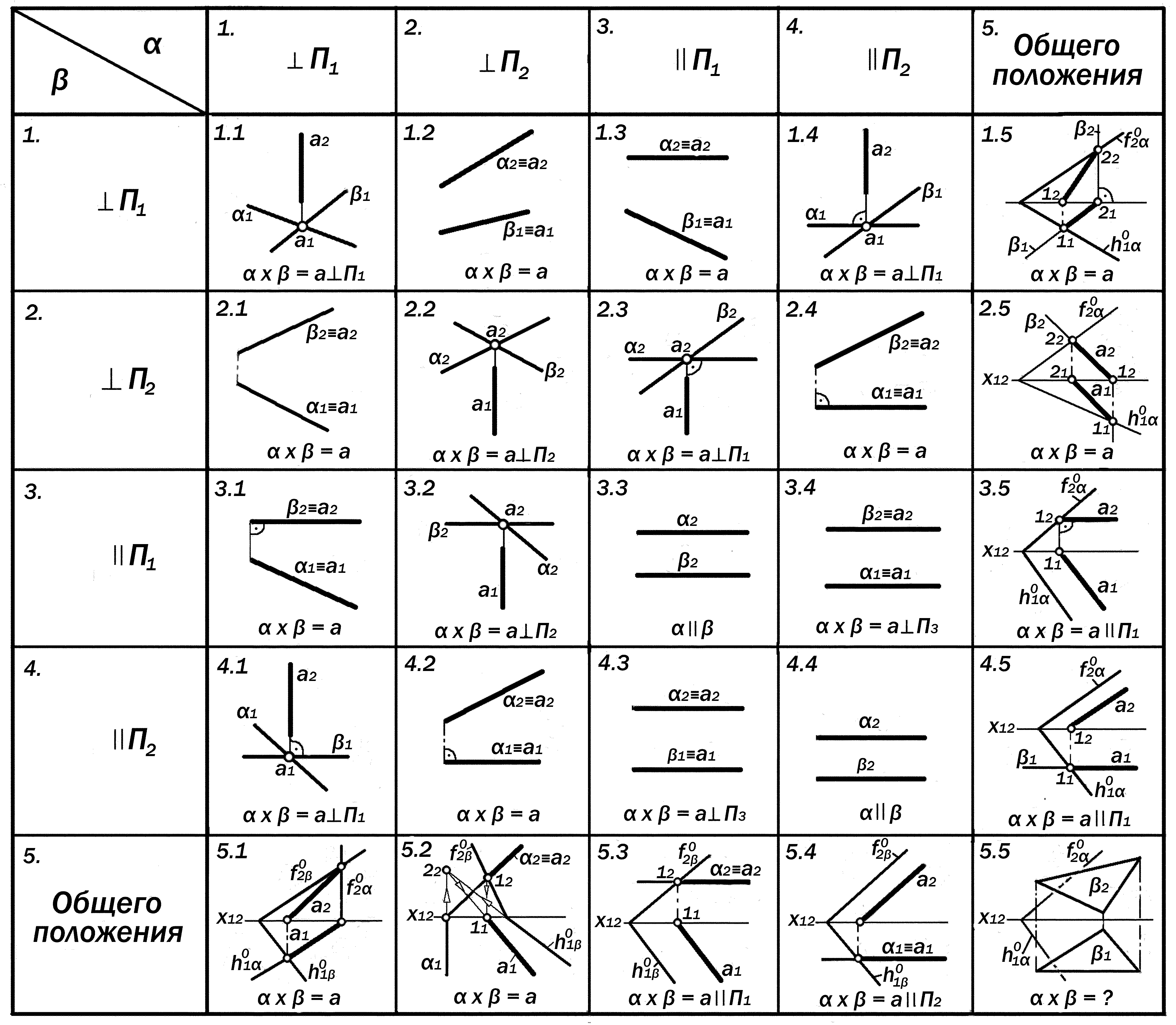
Такой анализ удобно производит на основе предлагаемой табличной фор-мы (так называемой таблицы Кэли) (рис. 10.11).
Рассмотрение этой таблицы приво-дит к следующим количественным и ка-чественным результатам:
Количественные результаты:
1. В 24 случаях из 25 возможных информация о виде взаимного располо-жения двух плоскостей присутствует на двухкартинном комплексном чертеже непосредственно, т.е., в этих случаях решение задачи содержится в условии и сводится к снятию необходимой ин-формации на основе понимания соби-рательных свойств вырожденных про-екций проецирующих плоскостей.
2. Из этих 24 случаев в двух слу-чаях (п.п.3.3. и 4.4.) две плоскости меж-ду собой взаимно параллельны, в двух
( п.п. 3.4 .и 4.3) взаимно перпендику-лярны, а в остальных, - взаимно пере-секаются.
|
|
Рис. 10.11. Варианты двухэлементных систем
взаимосвязанных плоскостей
Качественные результаты:
1. П1 (П2) П1(П2 ) х =
= аП1(П2) ; (п.1.1, 2.2);
2.П2( П1)П1(П2 ) х = а;
( п.1.2, 2.1);
3. || П1П1П1|| П1 х =
= а ||П1; ( п.1.3, 3.1);
4. || П2 (П1) П1 (||П2) х =
=аП1; ( п.1.4, 4.1);
5. П2 (||П2) || П2 (П2) х =
= а ||П2; (п. 2.4, 4.2);
6. || П1 ( П2 ) || П1 ( П2) ||
(п.3.3, 4.4)
7. || П1 (П2) || П2( П1) х =
=а || П1 (П2) П3 (п.3.4, 4.3);
8. ∦ П1 ( П2 )П1 ( П2), П2 ( П1)
х = а; ( п.1.5, 5.1);
9. П2 (о.п.) П2 (о.п.)
х = а; ( п.2.5.,5.2);
10. || П1(о.п.) (о.п.)|| П1 х =
= а || П1 ; ( п.3.5, 5.3);
11. (о.п.) || П2 (о.п.) || П1
х = а || П2; ( п.4.5, 5.4);
12. (о.п.) (о.п.) х = а; || ;
; .
Общие выводы из произведенного анализа:
1. Если две плоскости являются проецирующими одного направления, то они пересекаются по проеци-рующей прямой того же направления. В частности, такие плоскости могут быть параллельными и перпендикуляр-ными друг другу ( п.1.1, 2.2 );
2. Если две плоскости являются проецирующими разных направлений или одна из них занимает общее поло-жение, то они пересекаются по пря-мой общего положения (п.1.2, 2.1; 1.5, 5.1).
3. Плоскости уровня пересекают плоскости общего положение по их ли-ниям уровня ( п.1.3, 3.1, 4.2,2.4, 3.5, 5.3, 4.5, 5.4);
4. Если две плоскости параллельны одной из плоскостей проекций, то они параллельны между собой ( п. 3.3, 4.4 ).
5. Горизонтальная и фронтальная плоскости уровня пересекаются по профильно-проецирующей прямой
(п. 3.4,4.3 ).
6. Если обе плоскости занимают в пространстве общее положение, то они могут пересекаться по прямой об-щего положения, быть тождествен-ными, параллельными или перпендику-лярными.
Для установления конкретного вза-имного расположения двух плоскостей общего положения следует прибегать к помощи вспомогательных секущих пло-скостей частного положения, так как их вырожденные проекции, обладая соби-рательными свойствами, позволяют графически однозначно решить этот вопрос.