МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ “ЛЬВІВСЬКА ПОЛІТЕХНІКА”

Дослідження стійкості лінійних систем автоматичного регулювання Методичні вказівки

для самостійної підготовки та інструкція

до лабораторної роботи N 6

з дисципліни ‘ Теорія автоматичного керування ‘

для студентів базового напряму

6.0925 “Автоматизація та комп’ютерно-інтегровані технології”

Затверджено

на засіданні кафедри

автоматизації теплових

і хімічних процесів

Протокол N 14 від 30 березня 2006 р.

Львів - 2006

Дослідження стійкості лінійних систем автоматичного регулювання: Методичні вказівки для самостійної підготовки та інструкція до лабораторної роботи N 6 з дисципліни ”Теорія автоматичного керування” для студентiв базового напряму 6.0925 “Автоматизація та комп’ютерно-інтегровані технології”/ Укладачі: Г.Б. Крих, Ф.Д. Матіко, Р.Я. Дубіль. - Львiв: Вид-во Національного ун-ту ‘Львiвська полiтехнiка’, 2006. - 32 с.

Укладачi: Крих Г.Б., канд.техн.наук, доцент

Матіко Ф.Д., канд.техн.наук, доцент

Дубіль Р.Я., канд.техн.наук, доцент

Вiдповiдальний за випуск Пiстун Є.П., д-р техн. наук, професор

Рецензенти: Ділай І.В., канд. техн.наук, доцент

Фединець В.О., канд.техн.наук, доцент

Мета роботи: дослідити стійкість систем автоматичного регулювання (САР) за допомогою критеріїв Гурвіца та Найквіста, проаналізувати фактори, що можуть викликати втрату стійкості САР, дослідити вплив зміни параметрів елементів САР на її стійкість.

Необхідна теоретична підготовка: поняття стійкості динамічних систем, критерії стійкості систем.

Основні теоретичні відомості

1. Основи встановлення стійкості сар

Стійкість є однією з основних характеристик динамічних систем. Традиційно фізичну суть стійкості розглядають на прикладі кулі, розміщеної на поверхні (рис. 1). Під час дослідження стійкості такої системи її виводять із стану рівноваги і спостерігають за її поведінкою.

П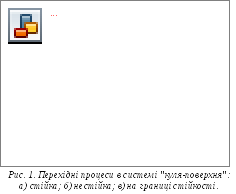рипустимо, що куля розміщена у впадині увігнутої поверхні (рис. 1, а). Стан рівноваги кулі в цьому положенні є стійким, оскільки після відхилення вона обов’язково повернеться до свого початкового положення. Навпаки, куля, розміщена у верхній точці опуклої поверхні (див. рис. 1, б), знахо-диться в нестійкому положенні. Дійсно, достатньо найменшого відхилення кулі від початкового положення, як вона скотиться по поверхні і не повернеться у вихідне положення. Якщо куля знаходиться на горизонтальній поверхні (рис. 1, в), то після її переміщення з початкової точки в іншу, вона не буде ні віддалятись, ні наближатись до початкового стану, тобто буде знаходитись на границі стійкості. На рис. 1 показані також відповідні перехідні процеси в системі куля-поверхня. Вони можуть бути коливними (див рис. 1, а), аперіодичними (див. рис. 1, б). Для системи (куля – поверхня) стійкість – це властивість повертатись у початковий стан після виведення її з цього стану та припинення дії збурення.

Таким чином, під стійкістю розуміють властивість системи повертатись до стану рівноваги після ліквідації збурення, що порушило стан рівноваги. Залежно від своїх властивостей система може бути стійкою, нестійкою або знаходитися на границі стійкості.

В розглянутих прикладах стійкість і нестійкість не залежать від початкових відхилень кулі. Розглянемо кулю, яка знаходиться на хвилястій поверхні (рис. 2). В цій системі при малих відхиленнях куля повертається в початковий стан, а при великих – не повертається. Така система є стійкою у малому і нестійкою у великому, тобто її стійкість залежить від величини початкового відхилення.

Стійкість є однією з основних вимог, що висуваються до систем автоматичного регулювання (САР). Стійка САР забезпечує зменшення різниці між заданим та поточним значеннями регульованої величини. Якщо ця різниця не зменшується в часі, а зростає, то система є нестійкою. Особливістю САР як динамічних систем є те, що САР із стійкими елементами може виявитись нестійкою, і навпаки САР із нестійкими елементами, наприклад із нестійким об’єктом регулювання, – може бути стійкою. Іншою особливістю реальних САР є те, що можливі декілька станів рівноваги.

В більш широкому розумінні стійкість системи автоматичного регулювання, оцінюється як її здатність повертатись до початкового незбуреного руху після припинення дії збурення. Стан рівноваги можна розглядати як найпростіший частковий випадок руху.

Загалом перехідний процес в системі залежить від властивостей системи та від вигляду збурення, тому в перехідному процесі х_вих(t) розрізняють дві складові:

• вільний рух системи , викликаний ненульовими початковими умовами при відсутності задаючих і збурюючих дій;

• вимушений рух , що залежить від вигляду збурюючої або задаючої дії.

Тобто

. (1)

Аналітичне формулювання стійкості записується у вигляді

. (2)

В стійкій САР відхилення регульованої величини від заданого значення з часом має стати менше деякого наперед заданого значення

,

де - допустима похибка регулювання.

Отже характер вільного руху САР визначає стійкість або нестійкість САР. Визначення стійкості САР – це є математична задача, для вирішення якої треба мати математичну модель системи (у вигляді диференціальних рівнянь, функції передачі, частотних характеристик тощо). Розглянемо, як математично можна встановити стійкість САР.

Нехай математична модель замкнутої САР задана у вигляді лінійного диференціального рівняння n-ого порядку з постійними коефіцієнтами

(3)

Для встановлення стійкості системи достатньо дослідити розв’язок однорідного рівняння

, (4)

характеристичне рівняння якого має вигляд

. (5)

У випадку, коли рівняння (5) має n некратних коренів , розв’язок однорідного рівняння (4) можна представити у вигляді суми

, (6)

де – і-й корінь характеристичного рівняння (5); – сталі інтегрування, що залежать від початкових умов. Згідно з умовою стійкості (2), САР буде стійкою, якщо буде задовольнятись умова

. (7)

Корені характеристичного рівняння (5) в загальному випадку можуть бути дійсними і комплексними спряженими. Розглянемо, як будуть змінюватись складові розв’язку рівняння (4) призалежно від значення і вигляду коренів. Дійсним коренямвідповідають складові загального розв’язку, які приз часом зменшуються за експонентою, а при- збільшуються, і при нульовому кореніскладова розв’язку є постійною і дорівнює. Графіки відповідних процесів показані на рис. 3, а. Комплексним кореням відповідає пара складових, суму яких можна записати у вигляді

^, (8)

де - нові сталі. На рис. 3, б показаний графік заникаючого коливного процесу, який відповідає наявності комплексного кореня з від’ємним значенням дійсної частини. Якщо дійсна частина, то процес є розбіжним коливним (див. рис. 3, в), і при наявності пари уявних коренів () встановлюються незаникаючі коливання з постійною амплітудою і частотою (див. рис. 3, г).

Нехай характеристичне рівняння містить m дійсних і відповідно (n-m) комплексних коренів. Тоді розв’язок однорідного диференціального рівняння (4) можна записати у вигляді

. (9)

Якщо всі m коренів є дійсними і від’ємними, то, оскільки кожна із складовихсуми приз часом зменшується до нуля. Якщо дійсні частинивсіх (n-m) комплексних коренів від’ємні, то, оскільки кожна із складовихдругої суми загального розв’язку (9) є заникаючим коливанням. Таким чином, для асимптотичної стійкості системи необхідно і достатньо, щоб всі дійсні кореніі дійсні частини всіх комплексних коренівбули від’ємними, тобто.

Рис. 3. Характер перехідного процесу для складових розв’язку з різними коренями характеристичного рівняння: а) дійсними (додатними, від’ємними, нульовим);

б) комплексними з від’ємною дійсною частиною; в) комплексними з додатною дійсною частиною; г) з уявними.

Якщо хоча б один дійсний корінь виявиться додатним або дійсна частина хоча б однієї пари комплексних коренів буде додатною>0, то відповідні їм складові розв’язку з часом будуть зростати і система в цілому буде нестійкою. Якщо в розв’язку один з дійсних коренівабо є пара уявних коренів (), а решта коренів є дійсними від'ємними або комплексними з від'ємною дійсною частиною, то система буде знаходитись на границі стійкості. За наявності нульового дійсного кореня ця границя називається аперіодичною, а за наявності комплексних коренів – коливною. За наявності кратних нульових коренів система буде нестійкою. Так, наприклад двом нульовим дійсним коренямвідповідають такі складові розв’язку:. Тобто припроцес є розбіжним і система в цілому також буде нестійкою.

Покажемо корені на комплексній площині (рис. 4). Щоб система була стійкою необхідно і достатньо, щоб всі корені характеристичного рівняння знаходилися зліва від уявної осі, тобто на лівій півплощині (рис. 4, а). Якщо хоча б один дійсний або хоча б одна пара комплексних коренів знаходяться на правій півплощині (рис. 4, б), то система буде нестійкою. Таким чином, стійкість системи визначається розміщенням коренів її характеристичного рівняння в комплексній площині. Отже, ліва півплощина є областю стійкості системи, а уявна вісь – границею стійкості.

Таким чином стійкість лінійних систем визначається стійкістю вільного руху системи і не залежить від вигляду і характеру зміни зовнішніх (збурюючих і задаючих) дій. Лінійна система, стійка при малих збуреннях, буде стійкою і при великих. Якщо динаміка системи точно описується диференціальним рівнянням (3), то стійкість в "малому" забезпечує необмежену стійкість системи. Нелінійні системи, що описуються нелінійними диференціальними рівняннями, можуть бути стійкими при малих збуреннях і нестійкими при великих.

Висновки щодо стійкості, розглянуті вище, стосуються лише лінійних систем. Однак реальні системи майже ніколи не бувають лінійними. На практиці їх досліджують за допомогою лінеаризованих диференціальних рівнянь. Правильність висновків про стійкість реальних систем за лінеаризованими рівняннями доведена А.М. Ляпуновим. Перша теорема А.М. Ляпунова доводить, що 1) якщо характеристичне рівняння лінеаризованої системи має лише від’ємні дійсні корені або комплексні з від’ємною дійсною частиною, то реальна система стійка. При цьому жодні відкинуті при лінеаризації члени з відхиленнями змінних у другому та вищих степенях не впливають на стійкість системи. 2) Якщо хоча б один дійсний корінь лінеаризованої системи є додатним або будь-яка пара комплексних коренів має додатну дійсну частину, то реальна система нестійка. 3) Якщо характеристичне рівняння лінеаризованої системи має хоча б один нульовий корінь або пару уявних коренів, то стійкість реальної системи не можна встановити за лінеаризованим рівнянням. В цьому випадку відкинуті члени з відхиленнями вихідної величини в степенях більших за одиницю докорінно змінюють опис динамічних процесів реальної системи.