1. Классическое определение вероятности, геометрическая вероятность. Действия над событиями

Основными понятиями в теории вероятностей являются понятия событияивероятности события.

Под событиемпонимается какой-либо результат эксперимента или наблюдения (испытания), который может произойти или не произойти. Появление какого-либо конкретного результата в одном испытании называетсяэлементарным исходом.

Все наблюдаемые нами события можно разделить на 3 вида: достоверные, невозможные, случайные.

Достоверным называется событие, которое обязательно произойдет при осуществлении определенной совокупности условий (в результате данного опыта). Например, выпадение менее шести очков при подбрасывании кости (кубика).

Невозможным называется событие, которое не может произойти при осуществлении определенной совокупности условий (в результате данного опыта). Например, появление белого шара из ящика, в котором лежат синие, красные и черные шары.

Случайнымназывается событие, которое в результате данного опыта может произойти, а может и не произойти. Например, попадание в цель при одном выстреле.

События называются несовместными, если появление одного из них в данном опыте исключает появление других событий в том же опыте. Например, извлечение стандартной и нестандартной детали при извлечении из ящика одной детали.

События называются равновозможными, если нет оснований отдать предпочтение одному из них. Например, выпадение «орла» и «решки» при подбрасывании монеты (если эта монета изготовлена из однородного материала).

Классическое определение вероятности.Вероятностью событияАназывается отношение числаm исходов, благоприятствующих этому событию, к числуnвсех равновозможных несовместных элементарных исходов:p(A)=m/n, где 0р(А)1.

При решении вероятностных задач часто используются формулы комбинаторики:

1. Перестановка из п элементов есть упорядочение этих элементов, то есть расположение этихпэлементов в определенном порядке.Число перестановокопределяется формулой

Р= n

2. Размещение из пэлементов покесть любой выборкэлементов, взятых в определенном порядке.Число размещенийопределяется формулой

3. Сочетание из пэлементов пок это любой выборкэлементов изп элементов безотносительно к порядку выбора.Число сочетанийопределяется формулой

Геометрическая вероятность

Пусть отрезок lсоставляет часть отрезкаL. На отрезокLнаудачу поставлена точка. Естественно считать, что вероятность попадания точки на отрезокl пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезкаL. Тогда вероятность попадания точки на отрезокl определяется равенством

Аналогично определяется вероятность попадания точки на фигуру f, составляющую часть фигурыF:

и вероятность попадания точки в пространственную фигуру g, которая содержится в пространственной фигуреG:.

Суммойдвух событий А и В называется событие С=А+В, состоящее в появлении события А или события В, или обоих вместе.

Произведением двух событий А и В называется событие С=АВ, состоящее в совместном появлении события А и события В.

Теоремы сложения и умножения вероятностей дают возможность наиболее простым способом решать задачи, в которых подсчет равновозможных и благоприятных элементарных исходов испытания был бы затруднителен или невозможен.

Теорема 1. Вероятность суммы несовместных событий равна сумме вероятностей этих событий

р(А+В)=р(А) + р(В).

Теорема 2. Вероятность суммы совместных событий вычисляется по формулер(А+В)=р(А) + р(В) – р(АВ).

Теорема 3. Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что имело место первое событие

р(АВ)=р(А)р(В/А)=р(В)р(А/В).

Следствие. Если события А и В независимы, тор(АВ)=р(А)р(В).

Совокупность нескольких событий, из которых хотя бы одно обязательно появится при проведении испытания, называется полной группой событий. Два события, образующие полную группу, называются противоположенными.

Сумма вероятностей противоположенных событий равна единице

.

1.1.На каждой из шести одинаковых карточек напечатана одна из букв: А, В, К, М, О, С. Карточки вынимают случайным образом по одной и располагают в ряд. Найти вероятность того, что: а) на первых четырех вынутых карточках можно будет прочитать слово КВАС; б) если разложить в ряд все шесть карточек, то можно будет прочитать слово МОСКВА.

Решение. а) Четыре карточки из шести можно выбрать числом способов, равных числу размещений из шести элементов по четыре. То есть,,m=1.

Тогда, согласно классическому определению вероятности

б) Число способов, которыми можно разложить все шесть корточек, будет равно числу перестановок из шести элементов: Р=6!=123456=720. Тогда, р=1/720.

1.2.В корзине 15 плодов, из которых 5 поражены болезнью. Из корзины наудачу берут 4 плода. Какова вероятность того, что: а) все взятые плоды будут здоровы; б) только 3 плода из 4 окажутся здоровыми?

Решение.а) Число способов, которыми можно выбрать 4 плода из 15, равно числу сочетаний из 15 по 4 -, а число способов, которыми можно выбрать только здоровые плоды, равно числу сочетаний из 10 по 4 -. Значит,и, соответственно

Тогда, согласно определению вероятности,

б) Выбор 3 здоровых плодов и одного пораженного может быть реализован способами, тогда==0,44.

1.3. Из колоды карт (36 карт) наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется только один туз.

Решение.Всего возможных разных комбинаций вынуть 3 карты из колоды в 36 карт -n==63534=7140. Одного туза мы можем выбрать=4 способами, две остальные карты можно выбрать=1631=496 способами. Итого, благоприятных вариантовm=4496=1984. Вероятность того, что среди трех карт окажется точно один туз, равнаp=0,2779.

1.4.В квадратном окне со сторонойаимеется квадратная форточка со сторонойв. Во время игры мяч случайно попадает в окно. Какова вероятность того, что мяч через открытую форточку влетит в комнату, не разбив окна? Какова вероятность, что окно разобьется?

Решение. А – событие, заключающееся в том, что окно не разобьется; В – окно разобьется.

Тогда, p(A)==; р(В)= 1- .

1.5.Три стрелка стреляют по мишени. Предполагается, что события попадания в мишень для стрелков независимы и вероятности их соответственно равны 0,9; 0,8; 0,7. Какова вероятность того, что: а) все три выстрела окажутся успешными? б) хотя бы один выстрел успешный? в) только один выстрел окажется успешным?

Решение. Событие А₁ – первый стрелок попал в мишень; р(А₁)= р₁=0,9;q₁= р()= 1 - р₁=0,1.

Событие А₂– второй стрелок попал в мишень; р(А₂)= р₂=0,8;q₂= р()=1 – р₂=0,2.

Событие А3 – третий стрелок попал в мишень; р(А₃)= р₃=0,7;q₃= р()= 1 – р₃=0,3.

а) Событие В – все три выстрела оказались успешными.

В=А₁А₂А₃ ; р(В)= р (А₁А₂А₃ )=р( А₁ )(А₂ )(А₃ ); р(В)=0,90,80,7=0,504.

б) Событие С– хотя бы один из выстрелов окажется успешным.

Р(С)=1-р()=1-0,10,20,3=0,994.

в) Событие Д - один выстрел оказался успешным, два неуспешными.

Р(Д)=р()+р()+р()=0,90,20,3+0,10,80,3+0,10,20,7= =0,092.

1.6.Из 30 экзаменационных билетов студент подготовил 25. Если он отказывается отвечать по первому взятому билету (которого он не знает), то ему разрешается взять второй. Найти вероятность успешной сдачи экзамена, если для этого студент должен ответить на первый билет, или, не ответив на первый, обязательно ответить на второй.

Решение. Событие А – первый билет «хороший», событие В – второй билет «хороший». Событие С – успешная сдача экзамена. Экзамен будет сдан, если произойдет событие А, или одновременнои В, то есть С=А+В.

Отсюда Р(С)=Р(А+В)=р(А)+р()р()=25/30+5/3025/290,977.

1.7.Фотограф взял с собой две плёнки, причем вероятность получения качественного негатива у одной 0.3, а у другой 0.8. Найти вероятность получения хорошего изображения, если фотограф зарядил аппарат на удачу выбранной плёнкой.

Решение. Событие А – событие, заключающееся в том, что получают хорошее изображение. Событие Н₁ - выбрана первая пленка, событие Н₂ – выбрана вторая пленка.

Р(Н₁)=р(Н₂)=0,5.

Тогда, р (А)=0.5*0.3+0.5*0.8=0.15+0.40=0.55.

1.8. Заяц проникает на огород, в котором находятся три овощехранилища. В первом-10 кочанов капусты и 10 морковин, во втором - столько же капусты и на пять морковин меньше, в третьем – капусты меньше в два раза, а моркови столько же, сколько и в первом овощехранилище. Какова вероятность того, что случайно съеденный овощ будет морковью.

Решение. А-событие, состоящее в том, что будет съедена морковь;

H₁-морковь из первого овощехранилища;

H₂-морковь из второго овощехранилища;

H₃-морковь из третьего овощехранилища;

р(H₁)= р(H₂)= р(H₃)=1/3;

р(А /H₁)= 1/2; р(А /H₂)= 5/15=1/3; р(А/H₃)= 2/3;

Тогда, р(А)= 1/3*1/2+1/3*1/3+1/3*1/3*2/3=1/2.

1.9. На картофельном поле работают три студенческие бригады. В первой бригаде 22 студента, во второй – 18, в третьей – 20. Вероятность выполнения плана первой бригадой – 0,8, второй – 0,7, третьей – 0,9. Найти вероятность того, что: а) наудачу выбранный студент является членом бригады, которая выполнила план; б) наудачу выбранный студент является членом первой бригады, при условии, что он является членом бригады, которая выполнила план.

Решение. а) Обозначим событие, состоящее в том, что план выполнила первая бригада через А₁, вторая бригада – А₂, третья – А₃. Вероятность выполнения плана первой бригадой обозначим р₁, второй – р₂, третьей – р₃. Тогда, р₁=0,8; р₂=0,7; р₃=0,9. Пусть событие Н₁ означает, что выбранный студент является членом первой бригады, Н₂ – второй бригады и Н₃ - третьей. Вероятности этих событий - р(Н₁)=, р(Н₂)=, р(Н₃)=.

Если наугад выбранный студент является членом бригады, выполнившей план, это означает появление одного из трех несовместных событий, т.е.

Р(А)= р₁ р(Н₁) + р₂ р(Н₂) + р₃ р(Н₃)=

б) Так как событие А (бригада выполнила план) уже произошло, то искомую вероятность определяем по формуле Байеса. Вероятность того, что наудачу выбранный студент является членом первой бригады:

1.10. Вини Пух в очередной раз падает с дерева. Учитывая большой опыт медвежонка в подобных мероприятиях, вероятность того, что он зацепится за сук равна 0,4, зацепится за сук или упадет на случайно проходящего Пятачка – 0,6, зацепится за сук, а затем упадет на Пятачка – 0,1. Найти вероятность того, что он упадёт на Пятачка.

Решение. А – Вини зацепится за сук; В – он упадёт на Пятачка.

Р(А)= 0,4; Р(А+В)= 0,6;Р(АВ)= 0,1;Р(В)= ?

0.6=0.4+Р(В)-0,1;Р(В)= 0,3.

1.11. Все грани игральной кости заклеивают разноцветной бумагой. 1-3-красной, 4-6-черной. При бросании кости выпала черная грань. Найти вероятность того, что на этой грани четное число.

Решение. А - событие, заключающееся в том, что выпадет четное число.

В - событие, заключающееся в том, что выпадет число очков большее трёх.

Тогда,

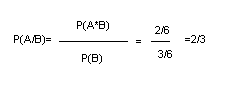
1.12. Вероятность поломки некоего прибора в любой момент времени Т равна р. Найти вероятность появления поломки в течение времени Т - t, если известно, что в течение времени Т t поломка не появилась.

Решение. А-событие, заключающееся в том, что поломка произойдёт в течение времени Т; В-событие, заключающееся в том, что поломка произойдёт в течение времени t.

Р(АВ)=Р(А) Р(В/А) т.к. Т включает в себя отрезок времени, равный t.

Р(А)-вероятность появления поломки в течение времени Т; р(А)=р.

Р(В)-вероятность появления поломки в течение времени t; р(В)=1-t*P/T;

Условная вероятность события В/А- р(В/А) =1-t/T т.е.

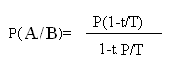
1.13.В компании 20 человек. Найти вероятность того, что все они родились в разные дни (365 дней, события равновероятны).

Решение. Для первого человека 365, для второго-(365-1), для третьего-(365-2), и т.д. для последнего-(365-20+1)=346 возможностей родиться в разные дни с другими, таким образом, число благоприятствующих исходов равно m = 365(365-1)…(365-20+1). При этом общее число вариантов равно n= 365²⁰ .

Тогда,

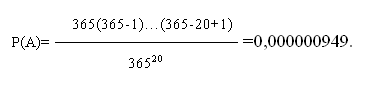
1.14.Стержень длинной L ломают на три части. Найти вероятность того, что из этих частей можно составить треугольник.

Решение.

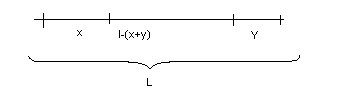
при этом 0«х«L и х+у«L.

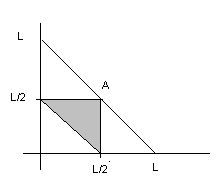т.о. в области треугольника ОLL любой разлом стержня приведёт к образованию треугольника.

х<L-x и y<L-y, откуда L-(x+y)<x+y т.е. каждая сторона треугольника должна быть больше суммы двух других отсюда два треугольника LLO и L/2L/2A; искомая вероятность равна

1.15.Монета номиналом в одну копейку имеет диаметр 1,5 см. Монету бросают на шахматную доску, при этом вероятность попадания на нее равна единице. Клетка доски имеет квадратную форму со стороной 2см. Какова вероятность того, что копейка попадёт ровно в клетку шахматной доски (разметку доски не учитывать).

Решение. Т.к. квадрат относительно мал, можно считать распределение вероятностей равномерным. При этом вероятность попадания центра монеты в какую-либо область квадрата пропорциональна площади этой области. Она равна площади области, делённой на всю площадь квадрата. В нашем случае необходимо, чтобы центр монеты попал в область центра квадрата, т.е.:

R=1.5/2. Легко найти сторону малого квадрата:

а=2-(1,5/2+1,5/2)=0,5. Т.к. вероятность пропорциональна площадям, то вероятность попадания монеты равна:

р(А)=S _max=(1/2)²=1/4.

1.16. Какой толщины должна быть монета, чтобы вероятность выпадения ее на ребро была равна 1/3.

Решение. Рассмотрим монету как вписанную в сферу, центр которой совпадает с центром тяжести монеты. Сама же монета есть цилиндр. Выберем на поверхности сферы точку А. Монета падает на ребро при условии, что радиус, проведённый в точку А, пересекает боковую поверхность данного цилиндра, т.е.:

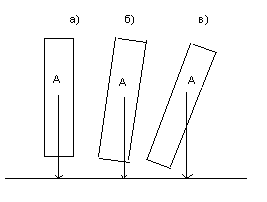В первых двух случаях монета упадёт на ребро, в последнем -на основание.

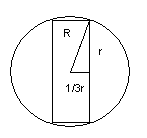R- радиус сферы; r-радиус монеты. По теореме Пифагора

R²=r²+1/9R²; откуда

R=; 1/3R0,354r. Таким образом, толщина монеты должна составлять около 35% её диаметра. (На практике это произойдёт только при падении на фиксирующую поверхность, например на поверхность, покрытую скотчем).

1.17. Из карточек разрезной азбуки составлено слово «СТАТИСТИКА». Затем из этих 10 карточек по схеме случайного выбора без возврата отобрано 5 карточек. Найти вероятность того, что из отобранных карточек можно составить слово «ТАКСИ».

1.18. Из 30 чисел (1,2,3,...,29,30) случайно отбирается 10 различных чисел. Найти вероятности событий: а) все числа простые; б) ровно 5 чисел делятся на 3; в) 5 чисел четных, 5 нечетных, причем одно число делится на 10.

1.19. Колода из 36 карт хорошо перемешена. Найти вероятности следующих событий: а) четыре туза расположены рядом; б) места расположения тузов образуют арифметическую прогрессию с шагом 7.

1.20. 25 участников годового собрания акционеров претендуют на посты председателя, секретаря, казначея и четырех других постов в правлении. Определите: а) сколько существует способов замещения вакантных мест претендентами; б) сколько существует способов замещения четырех остальных вакансий после избрания председателя, секретаря и казначея; в) сколько комитетов могут быть сформированы из 25 человек?

1.21.Из колоды карт (52 карты) наугад вынимают три (без возврата). Вычислить вероятность того, что среди вынутых карт будет один туз.

1.22.В ящикеабелых ивчерных шаров. Из него наудачу вынимают 2 шара. Найти вероятности того, что: а) оба шара белые; б) шары разного цвета.

1.23.Служащие одной из компаний распределены в таблице по отделам и полу:

подразделение	женщины	мужчины
производственный отдел	6	20
ремонтная мастерская	3	10
склады	5	5
автобаза	2	8
отдел реализации	5	10

Наудачу выбран один служащий. Найти вероятность того, что это: а) женщина; б) работник ремонтной мастерской; в) мужчина, работающий на складе; г) женщина, работающая на складе или автобазе; д) работник производственного отдела или отдела реализации.

В этой же компании решено организовать комитет из двух человек. Какова вероятность того, что они будут: е) женщины; ж) оба из производственного отдела; з) один из магазина, другой из автобазы; и) женщина из ремонтной мастерской и мужчина, работающий на складе; к) обе женщины, работающие на складе, или один человек из производственного отдела, а другой - мужчина, работающий в отделе реализации.

1.24.На курсах повышения квалификации бухгалтеров учат определять правильность накладной. В качестве проверки преподаватель предлагает обучающимся проверить 10 накладных, 4 из которых содержат ошибки. Он берет наугад из этих 10 две накладные и просит проверить. Какова вероятность того, что они окажутся: а) обе ошибочные; б) одна ошибочная, другая нет.

При условии, что обучающийся идентифицирует неправильную накладную с вероятностью 0,8, а правильную – с вероятностью 0,9. Какова вероятность правильной идентификации двух предложенных ему накладных, если: в) обе ошибочные; г) одна ошибочная, другая нет.

1.25. Магазин получает товар партиями по 100 штук. Если пять, взятых наугад, образцов соответствуют стандартам, партия товара поступает на реализацию. В очередной партии 8 единиц товара с дефектом. Какова возможность того, что товар поступит на реализацию.

1.26. К каждому из десяти этапов сборки станка прилагается документация. Для каждого этапа вероятность ошибки в документации составляет 0,002. Какова вероятность того, что документы: а) в полном порядке; б) имеется одна ошибка.

1.27. R,S,T– компоненты электронной системы. Вероятность бесперебойной работы каждого из компонентов в течение года 0,95; 0,9; 0,93 соответственно. а) Какова вероятность безотказной работы всей системы на протяжении этого срока, если необходимо, чтобы работали все 3 компонента; б) Допустим, достаточно, чтобы работали два из трех компонентов. Какова вероятность безотказной работы системы в этом случае?

1.28. В ящике 100 деталей, из них 10 бракованных. Наудачу извлечены 4 детали. Найти вероятность того, что среди извлеченных деталей: а) нет бракованных; б) нет годных.

1.29. В группе 12 студентов, среди которых 8 отличников. По списку наудачу отобраны 9 студентов. Найти вероятность того, что среди отобранных студентов 5 отличников.

1.30. Вычислить вероятность того, что при произвольном разбиении колоды из 52 карт на две части в каждой из них окажется по 13 черных и 13 красных карт.

1.31.На столе 10 книг, из которых 3 по теории вероятностей. Наудачу выбрали 6 книг. Найти вероятность того, что среди взятых книг: а) две книги по теории вероятностей; б) хотя бы одна по теории вероятностей.

1.32. На двух станках обрабатываются детали. Вероятность брака на первом – 0,03; на втором – 0,02. Первый станок обрабатывает вдвое больше деталей, чем второй станок. Вычислить вероятность того, что наудачу взятая деталь не будет бракованной.

1.33. Из урны, в которой 4 шара с номерами 1,2,3 или 123 вынимают один шар. СобытиеA_kсостоит в том, что на вынутом шаре окажется цифраk(k=1,2,3). Будут ли события A₁, A₂, A₃независимыми в совокупности.

1.34. Из урны, в которой 8 шаров с номерами 1, 2, 3, 12, 13, 20, 30 и 123 вынимают один шар. Событие A_k состоит в том, что на вынутом шаре окажется цифра k (k=0,1,2,3). Будут ли события A₁, A₂, A₃ независимыми?

1.35. Компания из четырех человек пытается поймать такси ночью. Вероятность поимки такси для каждого из них равна: 0.2, 0.4, 0.5, 0.8. Найти вероятность поимки такси.

1.36. В куче 20 кирпичей, из которых 14 с завода №1 ,а остальные с завода №2. При строительстве дома используется кирпич из данной кучи. Вероятность использовать кирпич с завода №1 - 0.8, №2-0.6. Какова вероятность использования кирпича из данной кучи.

1.37. У осуждённого на смерть появилась возможность остаться в живых, при попытке наугад достать платок из трёх сундуков - красного, черного, белого. Жизнь даруется в том случае, ели он достаёт зелёный платок. В ином случае он не остается в живых. Известно, что приоритеты перечисленных цветов определяются вероятностями выбора соответственно 0.7, 0.1, 0.2. В красном сундуке 3 зеленых и 3 синих платка, в черном 5 зеленых и 2 синих, в белом - 4 синих и зеленых. Найти вероятность того, что он не выживет.

1.38. Глава гильдии убийц решил убить неугодного ему короля и для этого послал трёх разбойников по очереди. Вероятность того, что придворный астролог предскажет нападение – 0.6. Если это произойдет, то охрана поймает нападающего с вероятностью 0.7. Король может защититься сам с вероятностью 0.2. Если астрологу не удастся предсказать нападение, то охрана поймает нападающего с вероятностью 0.4, а король может защититься сам с вероятностью 0.1. Найти вероятность того, что король будет убит.

1.39. Партизан пробирается в тыл врага. Вероятность того, что его заметят на первом посту 0,5, на втором-0,6. Вероятность его поимки на первом посту – 0,7, на втором 0,6. Найти вероятность его поимки.

1.40. Родители посылают сына купить продукты. На его пути 4 магазина. Вероятность того, что необходимые продукты есть в первом магазине равна 0,9, во втором-0,95, в третьем-0,8, в четвёртом-0,6. Какова вероятность того, что он вернётся ни с чем.

1.41. На столе лежит рыба, а за столом сидит человек и смотрит телевизор. Кот, воспользовавшись этим, пытается украсть рыбу со стола, при этом он делает три попытки. При каждой из них есть вероятность того, что хозяин заметит его и накажет. При первой попытке эта вероятность равна 0,2, при второй 0,3, при третьей-0,4. Найти вероятность того, что кот будет наказан (события независимы).

1.42. Курочка Ряба снесла яичко, а мышка его разбила. Курочка снесла ещё, но мышка разбила и это, наконец, она снесла 2 золотых. Вероятность того, что при падении скорлупа не выдержит и разобьётся, для первого яичка равна 0,7, для второго-0,8. Найти вероятность того, что дед и баба съедят:

а) одно яйцо всмятку,

б) глазунью из двух яиц,

в) останутся голодными.

1.43. По некоторому объекту произведен пуск двух ракет. Вероятность попадания в объект первой ракетой равна 0,8, второй – 0,7. Вероятность уничтожения объекта при попадании в него одной ракеты равна 0,4, а двух – 0,6. В результате пуска двух ракет объект был уничтожен. Найти вероятность того, что в объект попали две ракеты.

1.44. В семье двое детей. Найти вероятность того, что среди детей: а) все мальчики; б) хотя бы один мальчик. Вероятность рождения мальчика считать равной 0,5.

1.45. Подводная лодка может атаковать объект с одной из трех возможных позиций, занять которую она может с вероятностью р₁=0,3; р₂=0,5; р₃=0,2 соответственно. Вероятность уничтожения объекта с первой позиции – 0,3, со второй – 0,4, с третьей – 0,6. После атаки объект был уничтожен. Определить, с какой позиции вероятнее всего он был атакован?