36. Предмет и основные понятия теории игр

Во многих областях человеч. деятельности встречаются проблемы принятия управленческих решений в условиях неопределенности. При этом неопред-ть м.б. связана как с сознат. действиями конкурента, так и др. факторами, влияющими на эффект-ть принимаемого решения. Ситуации, в кот. эффект-ть принимаемого решения зависит от действий др. стороны, наз-ся конфликтными.

Теория игр- раздел математики, изучающий конфликтные ситуации на основе математич. моделей, т.е. это математ. теория, разрабатывающая оптимальн. правила поведения каждого из участников конфликтной ситуации.

Конфликт. ситуация наз-ся антогонистической, если увелич-е выигрыша одной из сторон на некот. величину приведет к уменьш-ю выигрыша др. стороны на такую же величину и наоборот.

Стороны, участвующие в игре наз-ся игроками.

Стратегия игрока- совок-ть правил, однозначно определяющих последоват-ть действий игрока в конкрет. ситуации. Стратегия игрока наз-ся оптимальной, если она обеспечивает данному игроку при многократном повторении игры max возможный средний выигрыш или min возможный средний проигрыш независимо от поведения конкурента.

Партией наз-ся каждый вариант реализ-и игры определ. образом. Выбор одной из стратегий и ее реализ-я наз-ся ходом. Ход наз-ся личным, если игрок сознательно выбирает стратегию. Ход наз-ся случайным, если выбор осущ-ся случайным механизмом.В завис-ти от кол-ва участников игры м.б. парными и множественными. В завис-ти от кол-ва стратегий: конечные, бесконечные.В конце партии каждый игрок A_i, i=1,m получает некоторую сумму a_i, кот. наз-ся функцией выигрыша (платежная ф-ция). Она может выражаться как количественно, так и выражением.

Если a_i>0, то это говорит о выигрыше i-го игрока. Если a_i<0 –о проигрыше. Если a_i=0 –ничейный исход.В завис-ти от вида ф-ции выигрыша игры подразделяются на матричные, биматричные, непрерывные, выпуклые и т.д.

37.Матр. игры с нулев. сумм. Будем рассм. парные игры, т.е. игры, в котор. из 2-х игр. А и В конеч. число стратег. В больш-ве случ. мы имеем игры с нулев. сумм., т.е. игры, в кот-ых выигр. одного игр. = проигр. другого. Парную конеч. игру удобно исслед., если она предст. в виде платеж. матрицы:

	В1	В2	…	Вn
А1	а11	а12	…	a1n
А2	а21	а22	…	a2n
…	…	…	…	…
Аm	am1	am2	…	amn

Здесь кажд. число а(ij), i=1,m , j=1,n явл-ся действит. числом и предст. собой сумму выигр., уплачив. игроком В игроку А, если игр. А выбир. стратегию, соотв-ую i-ой строке, а игр. В выбир. стратегию, соотв-ую j-ому столб. Такую игру назыв. матр-ой игрой mхn.

Целью участн. любой матр. игры явл. выбор наиб. выгодных стратег., к-ые доставл. игр. А макс. выигр., а игр. В миним. проигр.

Чистая стратег. Аi, i=1,m игр. А (чист. стратег. Bj, j=1,n игр. В) назыв. возм-ый ход игр. А(игр. В), выбран. им с вероятн. 1.

Если игра сост. из личных ходов, то выбор пары чистых стратег. (Аi, Вj) единств. образом опред-т исход игры.

Если же в игре испол-ся случ. ходы, то исход игры опред-тся мат. ожид.

Стратег. игр.А назыв. оптимальной, если при её примен-и выигр. игр.А не уменьш., какими бы стратег. не польз-ся игр.В.

Оптим-ой для игр.В назыв. стратег., при кот-ой проигр. игр.В не увелич-ся, какие бы стратег. не примен. игр.А.

38.Реш-е матр-х игр чистых стратег. Если игр.А имеет m стратег., а игр.В имеет n стратег., то для любой пары стратег. их чистые стратег. можно предст-ть в виде единич-х векторов. Напр., для пары стратег. (Аi,Вj) единич-ые вектора будут иметь вид:

pi=(0,…,0,1,0,…0), 1 – i-ое место; qj=(0,…,0,1,0…,0), 1-j-ое место.

При нахожд. оптим-ых стратег. игроки опираются на принцип осторож-ти, при к-ом игроки счит-ся одинаково разумными. Использ-я этот принцип найдем оптим. стратег. игр.АиВ.

Игр.А для каждой стратег. Аi, i=1,m сначала найдем миним. значен. ожидаемого выигр.

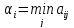i=1,m, затем, среди знач-ий αi-ых выберем максим.

Вел-на α назыв. нижней чистой ценой игры(максимино):

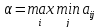
α – гарантир-ый выигр., к-ый может обесп-ть себе игр.А при любом поведение игр.В.

Стратег. ,j, обеспеч- ая получ-е нижней цены игры, назыв. макисм-ой стратег. Игр.В для каждой стратег.Вj, j=1,m выберет маским. знач-е:

Затем, из βj выберет миним. знач-е:

Аналог-но, стратег. , обеспеч-ая верхнюю чистую цену игры β назыв-ся миним. стратег.

Теорема: В матрич. игре нижняя цена игры не превосх-т верхней чистой цены игры:α≤β. Док-во: по опред-ию

Объед-м последние два соотн-я . Получим:

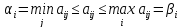
Отсюда 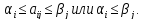Данное нерав-во справедливо при любых комбинац.i и j. Оно будет справедливо и для тех i и j, для к-ых

Значит, для этих i и j справед-во α≤β.

39.Игры с седловой точкой. Если в матр. игре нижн. и верх. чистые цены совпад-т, т.е. α=β, то такие игры назыв. играми с седловой точкой.

Знач-е ᴠ=α=β назыв. чистой ценой игры, а стратег. 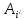иназыв. оптим. чистыми стратег-ми.

Пара чистых стратег. 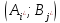назыв. седловой точкой матрич. игры.

Элемент 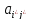назыв. седловым элем. платеж. матр.

Признаком матр. игры с седловой точкой явл-ся выраж-е

Элем. явл-ся наименш. в строке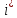и наибольш. в столбце с номером. Реш-ем явл-ся тройка чисел ().
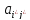