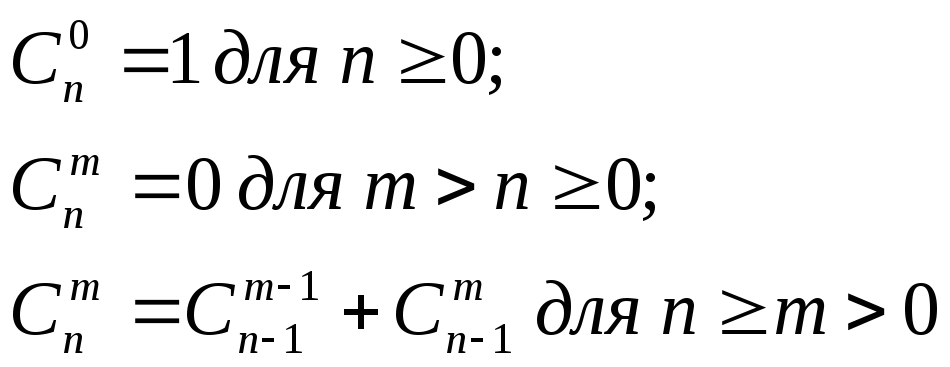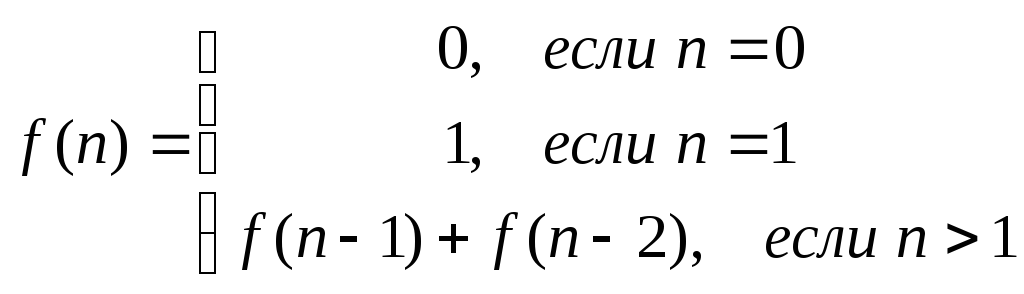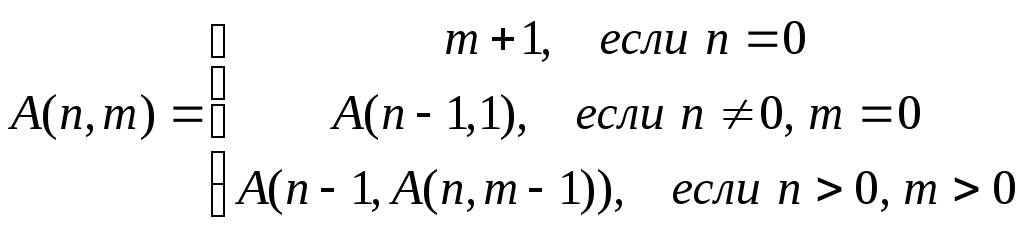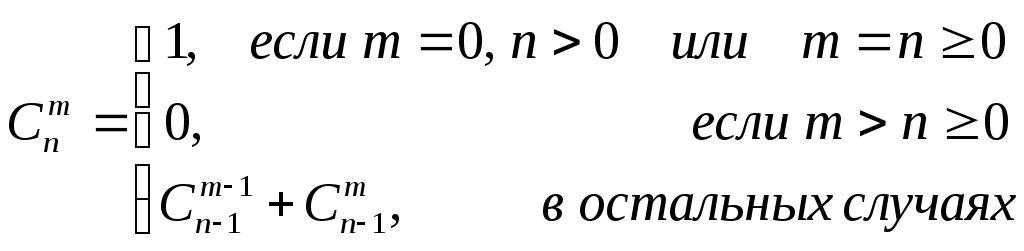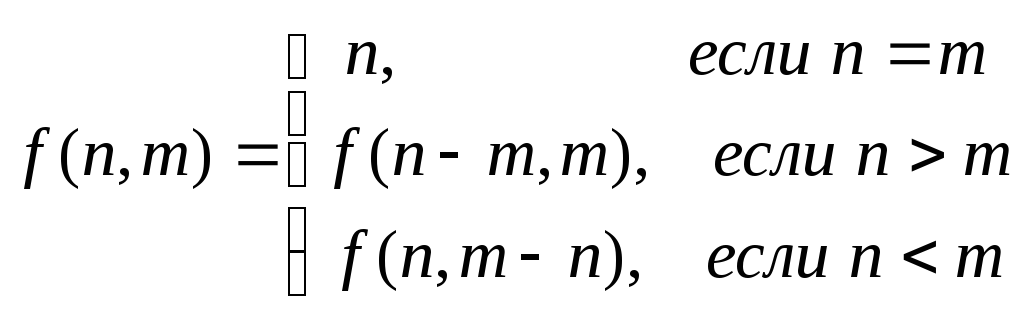3.4. Рекурсия более высокого порядка.

Используя более мощные виды рекурсии, можно записывать относительно лаконичными средствами и более сложные вычисления. Одновременно с этим, поскольку определения довольно абстрактны, растет сложность отладки и понимания программ.

Если в определении функции рекурсивный вызов является аргументом вызова этой же самой функции, то в такой рекурсии можно выделить различные порядки(order) в соответствии с тем, на каком уровне рекурсии находится вызов. Такую форму рекурсии называютрекурсией более высокого порядка. Функции, которые до сих пор определяли, были функциями с рекурсией нулевого порядка. В качестве классического примера рекурсии первого порядка часто приводится функция Аккермана:

A(m,n)=n+1 при m=0;

A(m,n)=A(m-1,1) при n=0;

A(m,n)=A(m-1,A(m,n-1)) в остальных случаях.

Кажущаяся простота этой функции обманчива. Вызов функции завершается всегда, однако ее вычисление довольно сложно, число рекурсивных вызовов растет лавинообразно уже при малых значениях аргумента.

В практике программирования рекурсий высокого порядка стараются избегать, разбивая определение на несколько частей и используя подходящие параметры для сохранения и передачи промежуточных результатов.

4. Рекурсия и итерация

Многие рекурсивные определения можно заменить нерекурсивными и организовать вычисления без использования рекурсии. В программировании есть два средства реализации повторяющихся вычислений (процессов):

• с помощью итерациив формецикла– последовательного повторения некоторого процесса до тех пор, пока не удовлетворится некоторое условие;

• с помощью рекурсии– вложения одной операции в другую, когда при отрицательном результате проверки условия выполнение процесса «приостанавливается» и происходит самовключение выполняемого процесса сначала уже в качестве подпрограммы для еще не выполненной до конца первоначальной подпрограммы.

Программы, использующие рекурсивные процедуры и функции, отличаются простотой, наглядностью и компактностью текста. Такие качества рекурсивных алгоритмов вытекают из того, что рекурсивная процедура (функция) описывает, что нужно делать, а нерекурсивная акцентирует внимание на том, как нужно делать. Итерация требует меньше места в памяти и машинного времени, чем рекурсия, которой необходимы затраты на управление стеком. Однако существуют некоторые функции, которые легко можно определить рекурсивно, но которые нельзя определить в терминах обычных алгебраических выражений, например,функция Аккермана. Для многих задач рекурсивная формулировка совершенно прозрачна, в то время как построение итерации оказывается весьма сложным делом.

Пример 7.Задача о ханойских башнях.Даны три столбика –A, B, C. На столбикеАодин на другом находятся 4 диска разного диаметра, и каждый меньший диск находится на большем. Требуется переместить эти четыре диска на столбикС, сохранив их взаиморасположение. СтолбикВразрешается использовать как вспомогательный. За один шаг допускается перемещать только один из верхних дисков какого-либо столбика, и больший диск не разрешается класть на диск меньшего диаметра.

Для определения подхода к решению поставленной задачи следует рассмотреть более общий случай с nдисками. Если будет сформулировано решение дляnдисков в терминах решения дляn-1дисков, то поставленная проблема будет решена, поскольку задачу дляn-1дисков можно будет, в свою очередь, решить в терминахn-2и т.д. до тривиального случая одного диска. А для случая одного диска решение элементарно: нужно переместить единственный диск со столбикаАна столбикС. Таким образом, будет получено рекурсивное решение задачи. Рассмотрим словесное описание алгоритма.

1. Если n=1, переместить единственный диск со столбикаАна столбикСи остановиться.

2. Переместить верхние n-1дисков со столбикаАна столбикВ, используя столбикСкак вспомогательный.

3. Переместить оставшийся диск со столбика Ана столбикС.

4. Переместить n-1дисков со столбикаВна столбикС, используя столбикАкак вспомогательный.

Рассмотрим программу Hanoi_Towers, которая решает поставленную задачу с помощью рекурсивной процедурыMove_Disks.

{Ханойские башни}

program Hanoi_Towers;

var n:integer;

{Рекурсивная процедура }

{ n – число дисков на столбике Source }

{ Source – исходный столбик }

{ Dest – столбик, на который нужно переставить диски }

{ Tmp – вспомогательный столбик }

procedure Move_Disks(n:byte;Source, Dest, Tmp:char);

begin {Move_Disks}

if n=1 then writeln(‘Переставить диск1 со столбика’, Source,’на столбик’, Dest)

else begin

{Переставляем n-1 верхних дисков с исходного столбика на }

{вспомогательный, используя диск как промежуточный}

Move_Disks(n-1, Source, Tmp, Dtst);

Writeln(‘Переставить диск’,n,’со столбика’,Source,

‘на столбик’,Dest);

{Переставляем n-1 дисков, расположенные на вспомогательном }

{столбике, на целевой, используя исходный диск как}

{промежуточный }

Move_Disks(n-1, Tmp, Dest, Source)

end

end; {Move_Disks}

{Основная программа}

begin {Hanoi_Towers}

write(‘Введите число дисков:’);

readln(n);

Move_Disks(n,’A’,’C’,’B’)

end. {Hanoi_Towers}

Нельзя, однако, рекомендовать применять рекурсию повсеместно, и, прежде всего, это касается традиционных вычислительных процессов, не являющихся существенно рекурсивными. И не столько из-за времени выполнения рекурсивных программ, сколько из-за сложности их отладки. Поэтому программист должен оценить, насколько целесообразно облегчать работу по написанию программы, подвергая себя при этом опасности усложнить отладку и резко увеличить время счета.

Индивидуальные задания

Для приведенных ниже заданий составить два варианта программы с использованием рекурсии и цикла и сравнить их.

№ варианта	З А Д А Н И Е
1.	Вычислить сумму 12 членов рекуррентной последовательности
2.	Вычислить функцию Бесселя 8-го порядка с аргументом x:
3.	Вычислить биноминальные коэффициенты для, если
4.	Определить 14-й член рекуррентной последовательности: a(N) – массив вещественных чисел.
5.	Дана последовательность Найти первое такое, что
6.	Вывести элементы массива в обратном порядке.
7.	Последовательность полиномов Лагерра определяется следующим образом:. Вычислить .
8.	Вычислить с погрешностью 10^-7.
9.	Определить в массиве максимальный и минимальный элементы.
10.	Определить сумму элементов данного массива.
11.	Дана функция . Вычислить корень уравненияf(x)=0 на отрезке (1,3) методом деления отрезка пополам с погрешностью .
12.	Вычислить значение факториала целого числа n, если известно, что:
13.	Вычислить значения n-го элемента последовательности чисел Фибоначчи, если существует такая зависимость:
14.	Вычислить площадь прямоугольника размером , воспользовавшись зависимостью:
15.	Вычислить значение функции Аккермана для двух неотрицательных целых чисел n и m, где:
16.	Вычислить значение квадрата целого положительного числа n, воспользовавшись зависимостью или Следует отметить, что в предложенном варианте вычисления квадрата целого числа используются только операции сложения и вычитания.
17.	Вычислить количество комбинаций из n разных элементов по m, т.е. количество неупорядоченных подмножеств из m элементов, которые принадлежат заданному множеству из n элементов , воспользовавшись зависимостью:
18.	Найти наибольший общий делитель двух положительных целых чисел n и m по алгоритму Евклида, воспользовавшись следующей зависимостью:
19.	Вычислить значения полиномов Эрмита: для заданного n>1.
20.	Вычислить с погрешность 10^-4 методом трапеций.
21.	Вычислить S1 - S2 , где S1 – сумма нечетных целых чисел от 2 до 22, S2 – сумма четных целых чисел от 5 до 17.
22.	Определить корень уравнения 2x+lg(2x+3)=1 методом Ньютона с погрешностью 10^-4 на отрезке [0, 0.5].
23.	Определить принадлежит ли заданные элемент массиву.
24.	Удалить из массива заданный элемент.
25.	Найти в упорядоченном массиве заданный элемент методом деления массива пополам (бинарный поиск).