Підручники з Дискретної Математики / DM / dm04

4. Подільність і факторизація

4.1. Подільність

Означення 4.1. Припустимо що a, b ∈ Z і a  0. Тоді a називають дільником b і позначають a | b, якщо c ∈ Z таке, що b = ac. В цьому випадку кажуть, що b є кратним a.

Приклад 4.1.1. Для кожного a ∈ Z \ {0} a | a і a | - a.

Приклад 4.1.2. Для кожного a ∈ Z 1 | a і -1 | a.

Приклад 4.1.3. Якщо a | b і b | c, то a | c.

Приклад 4.1.4. Якщо a | b і a | c, то  x, y ∈ Z, a | (bx+cy). Доведення базується на означенні дільника.

Теорема 4A. Припустимо, що a ∈ N і b ∈ Z. Тоді ! q, r ∈ Z такі, що b = aq + r і 0 ≤ r < a.

Доведення. Покажемо спочатку, що такі числа q, r ∈ Z існують. Розглянемо множину S = {b - as ≥ 0 : s ∈ Z}. Легко бачити, що S є не пустою підмножиною N ∪ {0}. Нехай r є найменший елемент S, а q ∈ Z є таке, що b - aq = r. Ясно, що r ≥ 0, залишається показати, що r < a. Припустимо протилежне, що r ≥ a. Тоді b - a(q +1) = (b - aq) - a = r - a ≥ 0, так що b - a(q +1) ∈ S. Але b - a(q +1) < r протирічить тому, що r є найменшим елементом S.

Далі покажемо, що такі елементи q, r ∈ Z єдині. Припустимо, що

b = aq₁ + r₁ = aq₂ + r₂ з 0 ≤ r₁ < a і 0 ≤ r₂ < a.

Тоді a|q₁ - q₂| = |r₂ - r₁| < a. Так як |q₁ - q₂| ∈ N ∪ {0}, повинно бути |q₁ - q₂| = 0, так що q₁ = q₂ , а отже і r₁ = r₂ .

Означення 4.2. Припустимо, що a ∈ N і a > 1. Тоді a називається простим, якщо існують всього два його додатні дільники, а саме 1 і a. Якщо існує більше ніж два додатні дільники числа a , то воно називається складним.

Зауваження. Число 1 не є простим, але не є і складним. Для цього єсть вагомі причини, як побачимо далі. В цій главі просте число будемо позначати літерою p.

Теорема 4B. Припустимо, що a, b ∈ Z, а p ∈ N є просте число. Якщо p | ab, то p | a або p | b.

Доведення. Якщо a = 0 або b = 0, то результат є очевидним. Без втрати загальності можна припустити, що a > 0 і b > 0. Припустимо, що p ł a. Нехай

S = {b ∈ N : p | ab і p ł b}.

Для доведення теореми досить показати, що множина S = Ø. Припустимо протилежне, що S  . Так як S  N, то S має найменший елемент, нехай це буде c ∈ N . Tоді

p | ac і p ł c.

Якщо p ł a, то c > 1. З другого боку c < p; при c = p не виконувалась би умова p ł c , а при c > p було б p | a(c - p), так що c - p ∈ S, а отже с не є найменшим елементом в S, що протирічить зробленому вище припущенню. Значить 1 < c < p. По теоремі 4А існують q, r ∈ Z такі, що p = cq + r і 0 ≤ r < c. Так як p є просте число мусить бути r ≥ 1, так що 1 ≤ r < c. В той же час ar = ap - acq, значить p | ar. Тепер маємо

p | ar і p ł r.

Але r < c і r ∈ N протирічить тому, що c є найменшим елементом S.

Застосовуючи теорему 4B скінчене число разів одержимо

Теорема 4С. Припустимо, що a1, . . , ak ∈ Z і p ∈ N є просте число. Якщо p | a1 . . ak, то p | a_j для деякого j = 1, . . . , k.

4.2. Факторизація

Ми вже звертали увагу раніше на те, що число 1 не вважаємо за просте. Наступна теорема виправдовує таке рішення. .

Теорема 4D. (Фундаментальна Теорема Арифметики). Припустимо, що n ∈ N і n > 1. Тоді n можна представити у вигляді добутку простих чисел, єдиним способом, з точністю до порядку множників.

Зауваження. Якби ми включили 1 в прості числа, то єдність розкладу числа на прості множники була б порушена, так як, наприклад, існувало б два представлення 6 = 2·3 = 1·2·3.

Доведення. Скористаємося методом математичної індукції. Почнемо з числа 2, яке є найменшим простим числом. Тепер припустимо, що n > 2 і кожне число m ∈ N в межах 2 ≤ m < n може бути розкладеним на прості множники. Якщо n є простим, то його можна вважати добутком простих чисел. Якщо ж воно не просте, то  n₁, n₂ ∈ N, такі, що 2 ≤ n₁ < n , 2 ≤ n₂ < n і n = n₁n₂. По нашій гіпотезі обидва n₁ і n₂ можуть бути представлені добутком простих чисел, а звідси слідує і розклад n на прості множники.

Тепер доведемо єдність розкладу. Припустимо

(1) n = p₁ . . . p_r = p’₁ . . . p’_s,

де p₁ ≤ . . . ≤ p_r і p’₁ ≤ . . . ≤ p’_s є прості числа. Так як p₁ | p’₁ . . . p’_s,, то по теоремі 4C p₁ | p’_j для деякого j = 1, . . . , s. Але з того, що p₁ і p’_j обидва прості числа, повинно бути p₁ = p’_j. Повторюючи ці міркування для для всіх простих множників числа n, прийдемо до висновку, що

r = s і p_i = p’_i для всіх i = 1, . . . , r.

Групуючи однакові прості множники можемо сформулювати теорему 4D наступним чином.

Теорема 4E. Припустимо, що n ∈ N і n > 1. Тоді n можна єдиним способом представити у вигляді

(2) n = p₁ ^m1 . . . p_r ^mr ,

де p₁ < .. . < p_r є прості числа, a m_j ∈ N для всіх j = 1, . . . , r.

Означення 4.3. Представлення (2) називається канонічним розкладом числа n.

4.3. Найбільший спільний дільник

Теорема 4F. Припустимо, що a, b ∈ N. Тоді існує єдине d ∈ N таке, що

(а) d | a і d | b;

(b) Якщо x ∈ N , x | a і x | b, то x | d.

Означення 4.4. Число d називається найбільшим спільним дільником чисел a і b і позначається

d = (a, b).

Доведення. Якщо a = 1 або b = 1, тоді d = 1. Припустимо, що a > 1 і b > 1. Нехай p₁ < .. . < p_r всі прості множники a і b. Тоді по теоремі 4E можна написати

(3)

де u₁, . . . , u_r, v₁, . . . , v_r ∈ N∪{0}. В представленнях (3), у випадку p_j не є простий множник, відповідні показники u_j або v_j рівні нулю. Тепер запишемо

Зрозуміло, що d | a і d | b. Припустимо, що x ∈ N і x | a та x | b. Тоді , де 0 ≤ w_j ≤ u_j і 0 ≤ w_j ≤ v_j для всіх j = 1, . . . , r. Зрозуміло, що x | d. Подібним же способом можна довести

Теорему 4G. Припустимо, що a, b ∈ N. Тоді існує єдине m ∈ N таке, що

(a) a | m і b | m;

(b) якщо x ∈ N і a | x та b | x, то m | x.

Означення 4.4. Число m називається найменше спільне кратне (НСК) a і b і позначається

m = [a, b].

Теорема 4H. Припустимо, що a, b ∈ N. Тоді існують x, y ∈ Z такі, що (a, b) = ax + by.

Доведення. Розглянемо множину

S = {ax + by > 0 : x, y ∈ Z}.

S є не пуста підмножина N і тому має найменший елемент, позначимо його d₀. Нехай x₀, y₀ ∈ Z такі, що d₀ = ax₀+by₀. Спершу покажемо, що

(5) d₀ | (ax + by) для будь яких x, y ∈ Z.

Припустимо протилежне, що (5) хибне. Тоді  x₁, y₁ ∈ Z такі, що d₀ ł (ax₁ + by₁). По теоремі 4А 

q, r ∈ Z такі, що ax₁ + by₁ = d₀q + r and 1 ≤ r < d₀. Tоді

r = (ax₁ + by₁) - (ax₀ + by₀)q = a(x₁ - x₀q) + b(y₁ - y₀q) ∈ S,

протирічить тому, що d₀ є найменшим елементом S. Залишається показати, що d₀ = (a, b). Візьмемо x = 1 і y = 0 в (5), тоді зрозуміло, що d₀ | a. Також при x = 0 і y = 1 в (5) одержимо, що d₀|b. З теореми 4F слідує, що d₀ | (a, b). З другого боку, (a, b) | a і (a, b) | b, так що (a, b) | (ax₀ + by₀) = d₀. Звідси слідує, що d₀ = (a, b).

Означення 4.5. . Числа a, b ∈ N називаються взаємно простими, якщо (a, b) = 1.

З теореми 4H слідує

Теорема 4J. Припустимо, що a, b ∈ N взаємно прості. Тоді  x, y ∈ Z такі, що ax+by = 1.

Для знаходження найбільшого спільного дільника (a, b) двох натуральних чисел a, b ∈ N можна слідувати доведення теореми 4F. Але для великих чисел з великою кількістю дільників це досит складно. Простіше використовувати наступну

Теорему 4K. (Алгоритм Евкліда) Припустимо, що a, b ∈ N і a > b. Припустимо далі, що q₁, . . . , q _n+1 ∈ Z і r₁, . . . , r_n ∈ N задовольняють умову 0 < r_n < r_n-1 < .. . < r₁ < b і

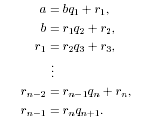
Тоді (a, b) = r_n.

Доведення. Спочатку покажемо, що

(6) (a, b) = (b, r₁).

Так як (a, b) | b і (a, b) | (a - bq₁) = r₁, то (a, b) | (b, r₁). З другого боку (b, r₁) | b і (b, r₁) | (bq₁ + r₁) = a, так що (b, r₁) | (a, b). Звідси й слідує (6). Подібним чином

(7) (b, r₁) = (r₁, r₂) = (r₂, r₃) = . . . = (r_n-1, r_n).

Але

(8) (rn-1, rn) = (rnqn+1, rn) = rn.

З (6)–(8) слідує результат теореми.

Приклад 4.3.1. Розглянемо (589, 5111). В наших позначеннях a = 5111 і b = 589. Тоді

5111 = 589 · 8 + 399,

589 = 399 · 1 + 190,

399 = 190 · 2 + 19,

190 = 19 · 10.

Звідси слідує, що (589, 5111) = 19. З другого боку,

19 = 399 - 190 · 2 = 399 - (589 - 399 · 1) · 2 = 589 · (-2) + 399 · 3 = 589 · (-2) + (5111 -. 589 · 8) · 3 = 5111 · 3 + 589 · (-26).

Звідси слідує, що x = -26 і y = 3 задовольняє 589x + 5111y = (589, 5111).

4.4. Елементарні властивості простих чисел

Фундаментальна теорема арифметики має багато наслідків Зараз ми приведемо один з них, що стосується простих чисел.

Теорема 4L. (Eвклід) Множина простих чисел нескінчена.

Доведення. Припустимо протилежне, що that p₁ < .. . < pr це всі прості числа. Нехай n = p1 . . . pr + 1. Тоді

n ∈ N і n > 1. З фундаментальної теореми арифметики слідує, що pj | n для якогось j = 1, . . . , r, так що

pj | (n - p1 . . . pr) = 1, що неможливо.

Проблеми для глави 4

1. Розглянемо числа 125 і 962.

a) Розкладіть на прості множники ці числа.

b) Знайдіть найбільший спільний дільник

c) Знайдіть найменше спільне кратне.

2. Розкладіть на множники число 6469693230.

3. Знайдіть (210, 858). Визначте x і y так, щоб (210, 858) = 210x + 858y. Звідси дайте формулу загального розв’язку вказаного рівняння в цілих числах.

4. Знайдіть (182, 247). Визначте x і y так, щоб (182, 247) = 182x + 247y. Звідси дайте формулу загального розв’язку вказаного рівняння в цілих числах.

5. Добре відомо, що числа кратні 2 закінчуються цифрами 0, 2, 4, 6 або 8, а числа кратні 5 закінчуються цифрами 0 або 5. Довести, що натуральне число кратне 3 тоді і тільки тоді, коли сума його цифр кратна 3. При доведенні слідуйте наступні кроки. Розглянемо число з к цифр x = x₁x₂ . . . x_k, де x₁, x₂, . . . , x_k ∈ {0, 1, 2, . . . , 9}.

a) Обчисліть значення x в термінах цифр x₁, x₂, . . . , x_k.

b) Знайдіть різницю між x і сумою його цифр.

c) Покажіть, що ця різниця кратна 3.

d) Закінчіть доведення.

6. Нехай x, y, m, n, a, b, c, d ∈ Z задовольняють умови m = ax + by і n = cx + dy з ad . bc = ±1. Довести, що

(m, n) = (x, y).