Студентам ИТ / 2 УПП_ИТ / Основн_литература / ИТ (Excel) / ИТ_прогноз_сост_ОУ

cov(St, St-1) = 1 cov(St, St) + 2 cov(St, St-1), cov(St, St-2) = 1 cov(St, St-1) + 2 cov(St, St).

Соответственно для автокорреляционных функций cork = cov(St, St-k)/cov(St, St) эти равенства дают так называемые уравне-

ния Юла-Уолкера
cor1 = 1 + 2 cor1,	cor2 = 1 cor1 + 2 ,	(1.1.16)
из которых определяются параметры АР(2)

1 = (cor1 - cor1 cor2)/(1- cor21), 2 = (cor2 - cor21)/(1- cor21). (1.1.17)

Для оценки параметров АР(2) по наблюдениям используют выборочные коэффициенты корреляции

	= n	St St k	/ n	S 2 .
cor					(1.1.18)
k	t 1		t 1	t

Идентификация РАР модели состояний ЭО при стационарных коэффициентах.

Используя метод наименьших квадратов, найдем коэффициенты РАР-модели типа (1.1.1) при всех известных значениях St и Ct (для упрощения управления C1t и C2t объединяются). Для этого будем минимизировать ошибку

СКО = n			(St m k St k			Ct )2			min.
		t 1			k 1
По аналогии с минимизацией (1.1.5) находим
уравнений для отыскания коэффициентов k и
m r n				St r St k	n	Ct St k n					St St k
r 1		t 1			t 1					t 1
m	r n			St rCt k	n		C	2 n		StCt ,
r 1		t 1			t 1			t	t 1

k = 1, 2, … m.

(1.1.19)

систему

, (1.1.20)

Полученная система m +1 уравнений решается численным способом.

11

Идентификация РАР модели состояний ЭО при нестационарных коэффициентах.

Решим задачу идентификации нестационарных параметров упрощенного аналога уравнения (1.1.1), так называемого, РАРуравнения 1-го порядка

St = t

St –1 + t Ct + Ht .

(1.1.21)

При этом зададим линейную регрессию структурных параметров

t = 0 + 1 t , t = 0 + 1 t.

(1.1.22)

Используя метод наименьших квадратов, получим систему уравнений, минимизирующую ошибку СКО

0 tnSt2 1 0 tnCt St 1 1 tntSt2 1 1 tntSt St 1 =

=tnSt St 1 ,

0 tnCt St 1 0 tnCt2 1 tntCt St 1 1 tntCt2 =

=tnStCt ,

(1.1.23)

0 tntS t2 1 0 tntSt St 1 1 tnt2St2 1 1 tnt2Ct St 1 =

=tntSt St 1 ,

0 ntS	Сt	0 ntС2		1 nt2S		Сt	1 nt 2C2		=
t t 1		t	t	t	t 1		t	t

= tntStCt .

Естественно, что «наилучшее», например по критерию R2 детерминации (см. стр. 16) или множественной корреляции, решение возможно получить при стохастическом характере помех,

т.е., когда Ht = Et.

Решив систему линейных уравнений (1.1.23) и воспользовавшись уравнением (2.2.11) при дополнительных предположениях (например, задав EVt, Pt и taxНДС), возможно найти, например, важные для задач аудита коэффициенты at , taxt .

12

Коррелированность стохастической помехи.

При оперативном прогнозировании достаточно сложной является проблема коррелированности (зависимости) соседних значений стохастической помехи, когда ряд Et стохастической

переменной сам описывается, например, моделью АР(1): Et =

= Et-1 + t , M( t) = 0, M( t t - k) = 2 k для t = 1, 2, .. , n. Для

«парирования» данной ситуации в современных статистических пакетах используется алгоритмический метод Кокрана-Оркатта, включающий следующие этапы.

1.Делаются оценки , β коэффициентов регрессии (1.1.4).

2.Вычисляются остатки Et = St – – β Ct .

3. По формуле (1.1.13) делается оценка			коэффициента
авторегрессионной зависимости Et = Et-1			+ t вычисленных
остатков.
4. Делается замена наблюдений
Ct = Ct – Ct-1 и St		= St – St-1.
Рассматривается новое регрессионное уравнение
St	= (1– ) +	Ct + t,	(1.1.24)

оценивание которого позволяет пересмотреть оценки и .

5. Повторно вычисляются остатки, и процесс возвращается к этапу 3.

6. Вычисления прекращаются, когда полученные оценки ρ

на последнем и предпоследнем циклах совпадают с заданной степенью точности.

1.2. Стратегическое планирование и прогнозирование.

Стратегическое планирование и прогнозирование связано с динамикой состояния ОУ в течение достаточно длительного

периода времени – 10 15 лет. Естественно, что на таком длительном периоде структурные параметры ОУ – коэффициенты динамического уравнения (1.1.2) – не могут оставаться постоянными – они подвержены либо некоторому тренду (Tr), либо сезонным и циклическим изменениям.

Считается, что тренд связан с долговременным воздействием (по сравнению с сезонными и циклическими колебания-

13

ми) на ОУ какого-либо плавно изменяющегося фактора, эффект от воздействия которого сказывается постепенно.

Обычно, исходя из знаний реальных условий, долгосрочный прогнозируемый период разбивают на периоды относительной стационарности структурных параметров и применяют к ним вышерассмотренные методы. Тем не менее, проблематичность стратегического прогнозирования легко пояснить с помо-

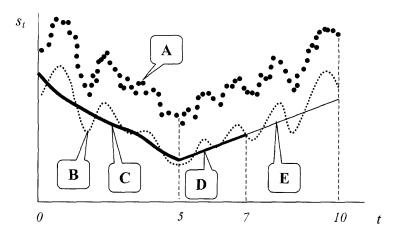
щью рис. 1.2.1.

Рис. 1.2.1

На рис. 1.2.1 приведен ряд А состояний некоторого ОУ для длительного периода (10 лет). Видно, что значения ряда подвержены сезонным и циклическим колебаниям. Ряд B получен из ряда А путем скользящего усреднения (сглаживания) последнего. В результате были устранены стохастические помехи. Кривые С и D, отвечающие различным периодам квазистационарности ОУ, построены с помощью оценивания нелинейных регрессионных зависимостей 3-го порядка на участке (0 5) лет и 1-го порядка на участке (5 7) лет. При этом сезонные колебания временно рассматривались как стохастическая помеха. На

участке (7 10) лет был сделан линейный постпрогноз (прогноз «задним числом») – линия E.

Заметим, что в стратегическом плане линейный прогноз верно отражает тенденцию увеличения значения прогнозируемого экономического показателя. В то же время, он проигрывает в плане долгосрочного прогнозирования, т.к. не отражает перио-

14

ды подъема и спада (два подъема и три спада). Однако ситуацию легко исправить, наложив на линейный прогноз колебательный компонент с сезонным периодом и амплитудой, оцененными по кривой B. Для этого надо вычесть из кривой B полученный тренд C+D и рассчитать требуемые параметры. В то же время видно, что спрогнозировать тренд (постепенное увеличение) се-

зонной амплитуды на участке (5 7) лет практически невозможно. Также невозможно по имеющимся данным сделать и настоящий прогноз за пределы 10 лет. Здесь может быть любая ситуация как подъема, так и спада технологического показателя. Заметим также, что использование линейной регрессии (вместо

нелинейной) на участке (0 5) лет не ухудшило бы полученный прогноз.

Из приведенного примера можно сделать важные выводы:

1.Линейный (полиномиальный) регрессионный анализ является самым простым и надежным методом отражения тенденций в стратегическом прогнозировании.

2.Линейный (полиномиальный) регрессионный анализ может быть легко скорректирован наложением сезонный компонент.

3.К прогнозу на длительный период нужно относиться скептически. Из практики считается, что прогноз возможен на период не более одной трети от периода имеющихся наблюдений.

4.Необходимо использовать некоторые формальные критерии качества регрессионных прогнозных моделей.

В общем случае для управления средствами в рамках стратегического планирования и прогнозирования необходимо использовать компьютерное имитационное моделирование, основанное на переборе возможных результатов, получаемых по моделям (1.1.1, 1.1.2) при различных структурных параметрах ОУ и помехах.

15

1.3.Критерии качества регрессионных моделей и прогнозирования.

Качество регрессионной модели определяют ее адекватностью исследуемому процессу, характеризуемой выполнением определенных статистических свойств и точностью или степенью близости к фактическим данным.

Модель (1.1.1, 1.1.2) является адекватной, если ряд остат-

ков St	– n k St k	n	kCt ,k Trt обладает свойствами
	k 1	k 1

случайности, независимости последовательных отсчетов и нормальности распределений.

Используют следующие критерии.

1) P-критерий поворотных точек (случайности ряда остатков), где количество P поворотных точек должно удовлетворять строгому неравенству для случайного ряда остатков

P > целая часть{2(n–1)/3 – 2[(16n – 29)/90]1/2}.

(1.3.1)

Каждый отсчет ряда остатков сравнивается с двумя рядом стоящими, если он больше или меньше их, то этот отсчет считается поворотным.

2) DW-критерий независимости (Дарбина-Уотсона)

DW = n	(Et	Et 1)2 / n	E2		2(1- n	Et Et 1	/ n	E2 ).
t 1		t 1	t	n	t 1		t 1	t
							(1.3.2)

DW стремится к 2 при независимости соседних отсчетов ряда остатков.

3) RS -критерий нормальности случайных остатков, где

RS = (Emax – Emin)/ [ n	E2	/(n 1)]1/ 2 .	(1.3.3)
t 1	t

RS характеризует попадание между табулированными границами с заданным уровнем вероятности (доверительный интервал) характеризует нормальность распределения ряда остатков.

Степень близости модели к фактическим данным характеризуется следующими критериями.

1) Детерминации (множественной корреляции) R2, где

R2 = 1 – n		/(n m 1) / n
	E2		(St S)2			/(n 2) .	(1.3.4)
t 1	t	t 1
		16

характеризует долю вариации зависимой переменной, объясняемой линейной регрессионной моделью (m – число независимых переменных, n – число наблюдений). Обычно 0,9 R2 < 1.

2) TS – статистика (Стьюдента), где
TS = β /D1/2( β ).	(1.3.5)

TS характеризует значимость оцениваемого коэффициента наклона в линейной регрессионной модели при заданном уровне (обычно 0,05), соответствующем доверительной вероятности 95 % и числе n – 2 степеней свободы.

3) F – статистика (Фишера), где
F = R2 (n – m – 1) /(1 – R2) m.	(1.3.6)

F используется для определения статистической значимости коэффициента детерминации R2 путем проверки гипотезы о равенстве нулю всех коэффициентов (за исключением свободного члена) регрессии.

4) Доверительный интервал прогноза S = Sn+T по линейной регрессионной модели будет иметь следующие границы

STmax = ST + ST			– верхняя граница,				(1.3.7)
STmin = ST – ST		– нижняя граница,
ST = TS [ n	E2		/(n 1) ]1/2 *
t 1		t
			*[1 +1/T + (Sn+T –	S	)2 / n				)2 ]1/2.
						(St		S
					t 1

Автоматизация прогнозирования ОУ по их РАР моделям поддерживается во многих современных статистических пакетах

(например, Statistica в среде Windows).

17

Вопросы для самопроверки к главе 1

1.В чем смысл прогнозирования состояний ОУ по его динамической модели.

2.Объясните смысл помех, описываемых сезонной, циклической и и стохастической компонентами вектора состояний ОУ.

3.Объясните модель парной линейной регрессии.

4.Объясните модель множественной линейной регрессии.

5.Чему равно математическое ожидание для стационарной авторегрессии первого порядка при отличном от 1 выборочном коэффициенте корреляции?

6.Как определяются параметры стационарной авторегрессии второго порядка?

7.Какой моделью обычно описывают коррелированную стохастическую переменную?

8.Чем отличаются оперативное и стратегическое прогнозирование?

9.Какой из регрессионных анализов является самым простым и надежным для отражения тенденций в стратегическом прогнозировании?

10.Какие критерии используют для оценивания адекватности регрессионных моделей?

11.Какими критериями пользуются дл оценивания степени близости регрессионных моделей к фактическим данным?

18

Глава 2. Прогнозирование состояний объектов управления на основе их стохастических моделей

2.1. Условные математические ожидания.

Не каждый ОУ может быть описан рассмотренными в главе 1 динамическими моделями. Часто возникают ситуации, когда по имеющейся информации (данным), например, совокупности X некоторого компонента вектора S состояния ОУ, требуется предсказать (оценить) некоторую величину Y, стохастически связанную с X. Стохастическая связь означает, что X и Y имеют некоторое совместное распределение Pr(X, Y). Причем, непосредственно величину Y измерить невозможно. Например, совокупность X может быть образована временным рядом S1, S2, … , st динамической переменной ОУ, а Y = St+T . Следовательно, есть величины, доступные измерению в некотором интервале времени, а прогнозу подлежат величины, связанные с будущим, невозможным наблюдению. Аналогичная ситуация встречается при многофакторном анализе, когда необходимо восстановить статистическую связь некоторого ненаблюдаемого параметра Y ОУ с N наблюдаемыми факторами X1, X2, … , XN .

В общем случае совокупность X: {X1, X2, …} некоторых случайных наблюдаемых величин называется предсказывающими или прогнозными переменными. Задача заключается в построении такой функции f(X) от этих величин, которую можно было бы использовать в качестве оценки для прогнозируемой величины Y. Функция f(X) должна быть «близка» по некоторой

мере сравнения (сходства) к величине Y, т.е. Y f(X). Такие функции f(X) называют предикторами величины Y.

В главе 1 был рассмотрен частный случай построения (синтеза) предикторов, когда была известна некоторая динамическая связь между прогнозными переменными. Когда такая дополнительная информация отсутствует, остается прибегнуть лишь к теории уловных математических ожиданий.

Совместное распределение Pr(X, Y) двух случайных величин X и Y подчиняется закону

Pr(x, y) = Pr(x) Pr(y x) = Pr(y) Pr(x y),

(2.1.1)

где Pr(y x) – условное распределение случайной величины Y (распределение Y при условии, что X = x); Pr(x y) – условное

распределение случайной величины X; Pr(x) = Pr(x, y) dy –

19

маргинальное распределение случайной величины X; Pr(y) =

= Pr(x, y) dx – маргинальное распределение случайной величины Y.

В качестве распределений Pr обычно рассматриваются плотности вероятности для абсолютно непрерывных величин и вероятности для дискретных. Для дискретных величин при вы-

числениях знак интеграла заменяется знаком суммы, т.е. . Из (2.1.1)следует, что

Pr(x y) = Pr(x, y) / Pr(y), Pr(y x) = Pr(x, y) / Pr(x).	(2.1.2)
Условное «матожидание» случайной величины Y
rY(x) = y Pr(y x) dy = y Pr(x, y) dy / Pr(x) =
= y Pr(x, y) dy / Pr(x, y) dy	(2.1.3)

называется функцией регрессии Y на X.

Условной дисперсией случайной величины Y называется

DY(x) = [y – rY(x)]2 Pr(y x) dy =
= [y – rY(x)]2 Pr(x, y) dy / Pr(x, y) dy.	(2.1.4)

Поскольку rY(x) и DY(x) являются случайными величинами, зависящими от x, то можно вычислить полные (безусловные) математическое ожидания и дисперсию случайной величины Y

Y = rY(x) ,

(2.1.5)

Y2 = D(y) = DY(x) = D(r) + D(y x) = R2 + YX2 .

где усреднение производится по случайной величине X. Выражение (2.1.5) следует из правила расчета дисперсий (см. «Основы информационных технологий автоматизированного управления», стр. 57 главы 2).

Выражение (2.1.5) показывает, что полная ошибка определения случайной величины Y складывается из ошибки определе-

ния регрессии r (среднего значения Y		при фиксированном зна-
чении случайной величины	X) и ошибки определения статисти-
ческой связи между Y и X.
Важное следствие из (2.1.5) заключается в том, что
2 = D (r) D(y) =	2 ,	(2.1.6)
R	Y

причем знак равенства выполняется лишь в случае, если

20