
- •1. Основные понятия и определения
- •2. Скорость фильтрации, Линейный закон Дарси.
- •3. Нелинейные законы фильтрации
- •4. Границы применимости закона Дарси.
- •Лекция 2
- •1. Дифференциальное уравнение движения
- •1. Установившиеся потоки флюида в пористой среде.
- •2. Характеристики одномерных фильтрационных потоков
Лекция 2
1. Дифференциальное уравнение движения
Аналитическое и численное исследование задач связано с применением основных законов течения в дифференциальной форме. Для процессов, происходящих в нефте-газовых пластах, характерно изменение основных параметров течения во времени. Такие процессы называются неустановившимися (нестационарными). Для получения дифференциальных уравнений движения выделяется бесконечно-малый элемент и рассматриваются законы сохранения массы, количества движения и энергии за бесконечно малый промежуток времени. При этом используются экспериментальные соотношения, определяющие зависимость силы трения, пористости и т.д. от параметров течения. Число уравнений должно равняться числу неизвестных параметров, что даёт замкнутую систему.
Для подземной гидромеханики характерно изотермическое изменение параметров вследствие значительных величин удельной поверхности коллекторов и их теплоёмкости. Т.о. для таких процессов можно не рассматривать уравнение энергии и ограничиваться уравнениями балланса массы (неразрывности) и движения.
Уравнение энергии необходимо рассматривать в локальных областях призабойной зоны из-за значительных перепадов давления, проявления дроссельного эффекта, а также при применении тепловых методов повышения нефте-газоотдачи.
Для замыкания системы уравнений необходимо введение замыкающих соотношений, а именно уравнений состояния флюидов и пористой среды. Кроме того для получения однозначного решения необходимо задание граничных и начальных условий.
В большинстве случаев решение задач подземной гидродинамике требует использования численных методов и только в сильно идеализированных случаях одномерного течения удаётся получить аналитическое решение.
Рассмотрим фильтрацию флюидов в пористых средах, принимая во внимание линейный закон Дарси.
Выделим два сечения – первое на расстоянии S от начала отсчета вдоль линии тока, второе – на расстоянии S от первого (рис. 1).
Движение флюида
происходи в направлении возрастания
координаты S.
В сечении с координатой S
обозначим приведенное давление через
p*(S,
t),
в сечении координат S
+ S
– через p*(S
+ S
,t),
используя формулу
![]() ,
,
п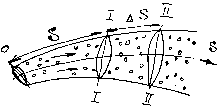 олучаем
олучаем
![]() ,
(20)Рис.
1.Трубка тока
,
(20)Рис.
1.Трубка тока
или перейдем к
пределу при
![]() ,
,
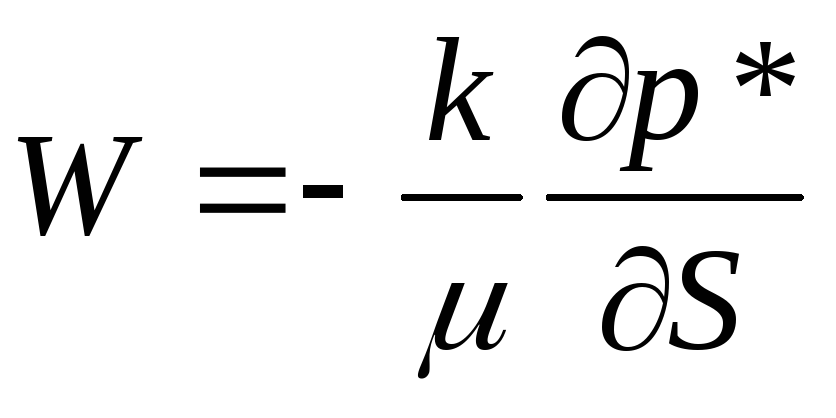 ,(21)
,(21)
Знак (-) в
правой части означает, что приведенное
давление падает по движению жидкости,
т.е. градиент приведенного давления
отрицателен
![]() .
.
Формула (21)
справедлива только для изотропной
среды, для которой характерно постоянство
проницаемости по всем направлениям в
окрестности рассматриваемой точки.
Однако с переходом от точки к точке
пласта проницаемость может и изменяться,
таким образом
![]() (модель изотропного неоднородного
пласта).
(модель изотропного неоднородного
пласта).
Запишем уравнение
(21) в проекциях на оси координат x,
y,
z.
Если обозначить через ![]() ,
,![]() ,
,![]() единичные векторы
вдоль осей координат, вектор скорости
фильтрации можно записать в виде
единичные векторы
вдоль осей координат, вектор скорости
фильтрации можно записать в виде
![]() ,
(22)
,
(22)
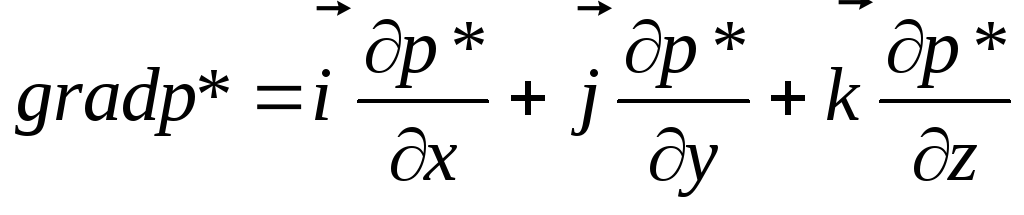 ,(23)
,(23)
тогда
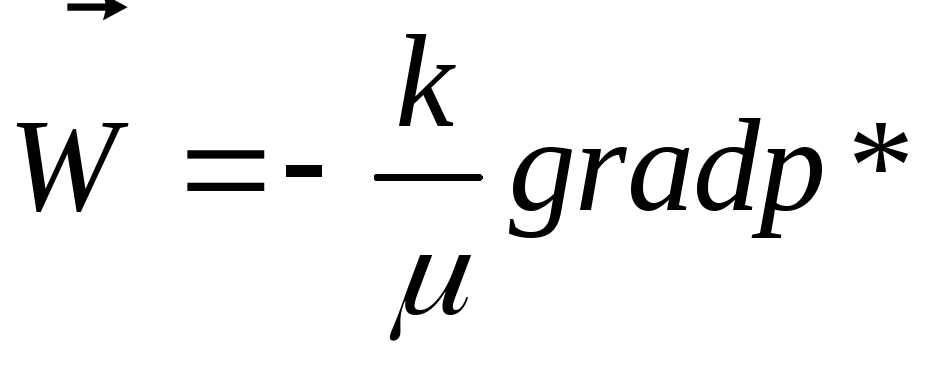 ,
(24)
,
(24)
или в проекциях на оси координат
 ,
,
 ,
,
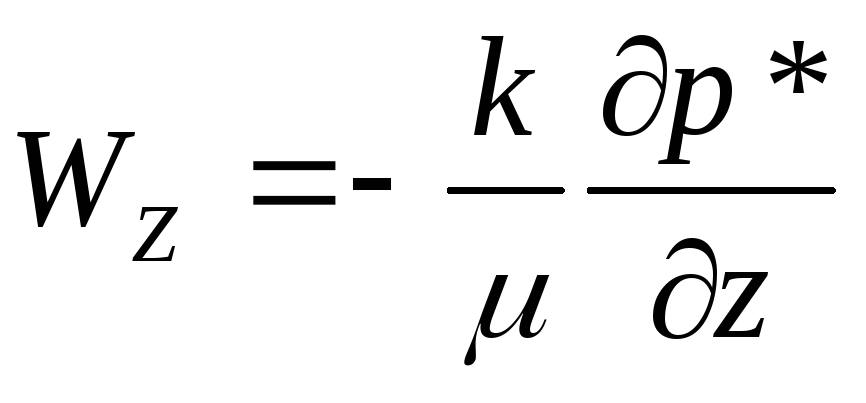 ,
(25)
,
(25)
если ось z
направлена вверх ![]() и дифференциальные уравнения движения
примут вид
и дифференциальные уравнения движения
примут вид
![]() ,
,![]() ,
,
![]() ,
(26)
,
(26)
в векторной форме
![]() .
(27)
.
(27)
В дифференциальной
форме двучленный закон записывается в
виде ![]() ,
(28)
,
(28)
где S – координата, взятая вдоль линии тока по движению жидкости.
В векторной форме двучленный закон выведен из теории размерностей, в виде
![]() (29)
(29)
В прекциях на оси координат имеем
![]() ,
(30)
,
(30)
![]() ,
,
![]() .
.
При фильтрации
неньютоновских вязкопластичных
жидкостей, а также при фильтрации с
очень малыми скоростями имеет место
закон фильтрации (5), который отличается
от закона Дарси наличием предельного
градиента
![]() ,
по достижении которого начинается
движение. В векторной форме закон
фильтрации с предельным градиентом
выведен из теории размерностей и имеет
вид
,
по достижении которого начинается
движение. В векторной форме закон
фильтрации с предельным градиентом
выведен из теории размерностей и имеет
вид![]() .
(31)
.
(31)
![]() ;
(32)
;
(32)
в проекции на оси координат:
![]() ;
(33)
;
(33)
![]() ;
;
![]() .
.
Лекция 3.
Вывод дифференциального уравнения неустановившейся фильтрации однородного флюида по закону Дарси. Функция Л. С. Лейбензона.
Для вывода дифференциального уравнения неустановившейся фильтрации используем уравнение неразрывности
![]()
или
![]() (34)
(34)
Сумма в скобках в
левой части уравнения (34) представляет
собой дивергенцию вектора скорости
фильтрации
![]() и кратко записывается таким образом:
и кратко записывается таким образом:
![]() ,
(35)
,
(35)
поэтому уравнение (34) можно записать в виде:
![]() .
(36)
.
(36)
Уравнение (34) (или
36) справедливо только в том случае, если
внутри объема
![]() нет источников или стоков, выделяющих
или поглощающих флюид, не происходит
химических реакций, фазовых превращений
и т.д.
нет источников или стоков, выделяющих
или поглощающих флюид, не происходит
химических реакций, фазовых превращений
и т.д.
И уравнения движения

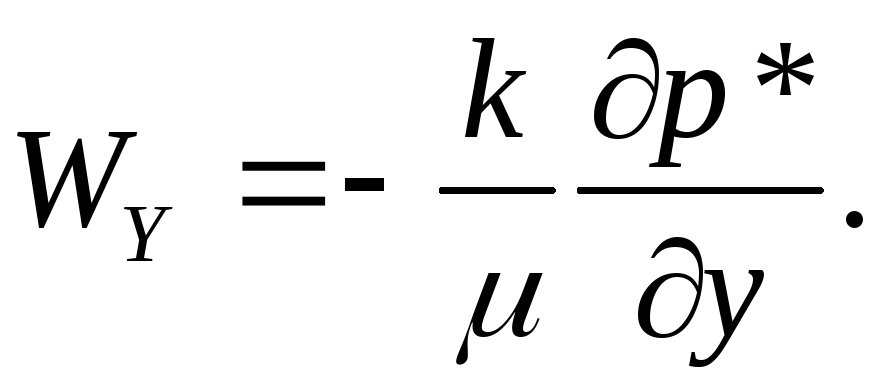
 (37)
(37)
В уравнении (11) не будем учитывать силу тяжести.
Введем функцию
![]() (функцию Лейбензона), тогда дифференциал
этой функции равен:
(функцию Лейбензона), тогда дифференциал
этой функции равен:
![]() ,
(38)
,
(38)
тогда
![]() ,
(39)
,
(39)
т. к. функция Лейбензона и давление зависит от координат x,y,zи времениt, то (38) можно записать в развернутом виде, используя понятие полного дифференциала функции от многих переменных:
![]() .
.
Сравнивая коэффициенты при x,y,z получаем:
![]() ,
,
![]() ,
,
![]() ,
(40)
,
(40)
Запишем выражение для составляющих массовой скорости фильтрации, умножив правую и левую части уравнения (37) на плотность и используя соотношения (40):
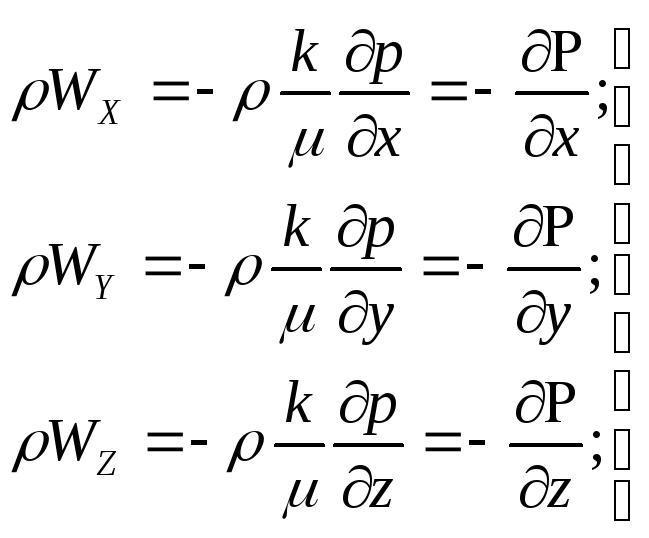 ,
(41)
,
(41)
Подставим выражение (41) в уравнение неразрывности (34), получим:
![]() (42)
(42)
или
![]() ,
(43)
,
(43)
где
![]() - оператор Лапласа от функции Лейбензона
(39).
- оператор Лапласа от функции Лейбензона
(39).
Уравнение (42) справедливо для неустановившегося движения однородного флюида в однородной пористой среде по закону Дарси.
При установившейся
фильтрации
![]() и будет удовлетворяться уравнение
Лапласа для функции Лейбензона:
и будет удовлетворяться уравнение
Лапласа для функции Лейбензона:
![]() (44)
(44)
При k=const,=const, и![]() ,
тогда можно ввести функцию Лейбензона
в виде:
,
тогда можно ввести функцию Лейбензона
в виде:
![]() .
(45)
.
(45)
Тогда дифференциальное уравнение неустановившейся фильтрации примет вид:
![]() .
(46)
.
(46)
Выразим функцию Лейбензона (45) через давление для различных флюидов – несжимаемой жидкости, упругой жидкости, совершенного газа и реального газа. Для этого в (45) подставим соответствующие выражения для плотности и проинтегрируем.
Для несжимаемой жидкости о=const, тогда
![]() ,
(47)
,
(47)
т. е. функция Лейбензона пропорциональна давлению.
Для упругой жидкости:
![]() ,
(48)
,
(48)
т. е. имеем тот же вид, что и для несжимаемой жидкости.
Для совершенного газа с уравнением состояния
![]() ,
(49)
,
(49)
получаем
![]() ,
(50)
,
(50)
т. е. функция Лейбензона пропорциональна квадрату давления.
Для реального газа с уравнением состояния
![]() ,
(51)
,
(51)
тогда
![]() ,
(52)
,
(52)
т. е. функция Лейбензона записывается в виде интеграла.
Т. к. реальные свойства газа проявляются при высоких пластовых давлениях, то в этом случае оказывается существенной зависимость вязкости от давления и нужно использовать функцию Лейбензона в виде (39).
Лекция 4.
