7. Общая постановка задачи проверки гипотез. Параметрические и непараметрические статистические критерии.

Общая постановка задачи проверки гипотез:

1. Формулируют (выдвигают) нулевую гипотезу H₀ об отсутствии различий между группами, об отсутствии существенного отличия фактического распределения от некоторого заданного, например, нормального, экспоненциального и др.

Сущность нулевой гипотезы H₀: разница между сравниваемыми генеральными параметрами равна нулю, и различия, наблюдаемые между выборочными характеристиками, носят случайный характер, то есть эти выборки принадлежат одной генеральной совокупности.

2. Формулируют противоположную нулевой, альтернативную гипотезу H₁.

3. Задают уровень значимости α. Уровень значимости α – это вероятность ошибки отвергнуть нулевую гипотезу H_0, если на самом деле эта гипотеза верна. При α≤0,05 ошибка возможна в 5% случаев.

4. Для проверки выдвинутой гипотезы используют критерии.

Критерий – это случайная величина К. которая служит для проверки H₀. Эти функции распределения известны и табулированы. Критерий зависит от двух параметров: от числа степеней свободы и от уровня значимости α. Фактическую величину критерия получают по данным наблюдения К_набл.

5. По таблице определяют критическое значение, превышение которого при справедливости гипотезы маловероятно К_крит(α,f).

6. Сравнивают К_набл и К_крит(α,f).

Если К_набл> К_крит(α,f), то отвергают H₀ и принимают H₁.

Если К_набл<К_крит(α,f), то принимают H₀.

Это для параметрических критериев.

Если использованы непараметрические критерии, то наоборот: если К_набл> К_крит(α,f), то принимают H₀.

7. Вывод: различие статистически значимо (α≤0,05) или незначимо.

Параметрические критерии представляют собой функции параметров данной совокупности и используются, если совокупности. Из которых взяты выборки, подчиняются нормальному закону распределения.

Непараметрические критерии применяются, если нет подчинения распределения нормальному закону. Эти критерии обычно заменяют данные выборки знаками (+ или -), рангами (т.е. числами 1; 2; 3;…, описывающими их положение в упорядоченном наборе данных), категориями и т.п. Непараметрический критерий можно использовать, если объем выборки небольшой настолько, что невозможно оценить закон распределения данных.

8. Проверка гипотез относительно генеральных средних и относительно генеральных дисперсий.

ОТНОСИТЕЛЬНО СРЕДНИХ:

Предположим, что надо сравнить состояние больных до и после лечения. Для этого сравнивают друг с другом две независимые выборки объемом n₁ и n₂, взятые из нормально распределенных совокупностей с параметрами M(X₁) и M(X₂). Дополнительно предполагаем, что независимые генеральные дисперсии равны между собой. По этим выборкам найдены соответствующие выборочные средние 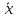₁ и 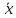₂ и исправленные дисперсии S₁² и S₂². Уровень значимости задан.

1. Нулевая гипотеза H₀: M(X₁)=M(X₂).

2. Конкурирующая гипотеза H₁:M(X₁)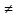M(X₂).

3. Для проверки нулевой гипотезы в этом случае можно использовать критерий Стьюдента сравнения средних.

Величину критерия находим по формуле:

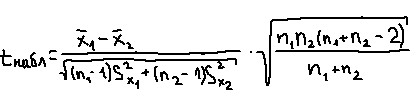
Обычно расчет ведется на ЭВМ.

Доказано, что величина t_набл при справедливости нулевой гипотезы имеет t-распределение Стьюдента с f=n₁+n₂-2 степенями свободы

4. По таблице находим t_крит (α.f=n₁+n₂-2).

5. Сравниваем t_крит и t_набл

Если |t_набл|<t_крит(α, f)=>H₀.

Если наоборот, то отвергается Н₀ и принимается H₁, различие достоверно.

ОТНОСИТЕЛЬНО ДИСПЕРСИЙ:

Пусть генеральная совокупность Х₁ и Х₂ распределены нормально. По независимым выборкам объемом n₁ и n₁, извлеченных из этих совокупностей, найдены исправленные выборочные дисперсии S_x1² и S_x2². Требуется сравнить эти дисперсии. При заданном уровне значимости α, надо проверить нулевую гипотезу о равенстве генеральных дисперсий нормальных совокупностей.

1. Н₀: σ_х1²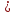σ_х2².

2. Н₁: σ_х1²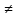σ_х2².

3. В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий используем случайную величину F, равную отношению большой исправленной выборочной дисперсии к меньшей F_набл=S_б²/S_м².

4. Величина F, при условии справедливости нулевой гипотезы, имеет распределения Фишера-Снедекора со степенями свободы f₁=n₁-1 и f₂=n₂-1, где n₁ – это объем выборки, по которой вычислена большая выборочная дисперсия.

Из таблицы находим F_крит(α, f₁, f₂).

5. Сравниваем F_набл< F_крит(α, f₁, f₂)=>H₀, генеральные дисперсии различаются не значимо.