Ekzamen_mat_metody

Примеров геологических задач:

1. Установить влияние выветривания на изменение содер­жаний элемента А в изучаемых породах 2. Определить влияние веса пробы и способа ее отбора на изменение содержаний разведываемого компонента.

3. Установить влияние состава пород, трещин различной ориентировки, разрывных нарушений на формирование оруднения.

Если количество значений случайной величины на раз­ных уровнях всех факторов одинаково, то дисперсионный ана­лиз называют равномерным, если различное — неравномер­ным. Как и при решении других задач статистическими мето­дами, при дисперсионном анализе формулируется предполо­жение о том, что фактор или их вза­имодействие не оказывают существенного влияния на изме­нение величины X.

Если на случайную величину действуют взаимонезависимые факторы А и Б, то общую дисперсию этой случайной величины ² можно рассматривать как сумму дисперсий:

Тре­бование нормальности выборочного распределения допускает некоторые отклонения, так как критерий Фишера, используе­мый в дисперсионном анализе, применим и к распределени­ям, отличным от нормальных

В зависимости от количества учитыва­емых факторов различают однофакторный, двух- и многофакторный дисперсионный анализ. Каждый фактор представляет собой переменную величину, изменяющуюся дискретно или непре­рывно.

Однофакторный

С его помощью осуществляется проверка гипотезы об однородности нескольких независимых выборок.

При равномерном однофакторном дисперсионном анализе случайной величины х относительно фактора А, имеющего k уровней при количестве замеров на каждом уровне равном n, результаты наблюдений обозначаются как x_ij, где i—номер наблюде­ния (i=1, 2, .., n), a_j—номер уровня фактора (j=1, 2, .., k).

По этим данным рассчитываются следующие статистики:

1) общая сумма 

2) факторная сумма

 

3) остаточная сумма 

4) общая, факторная и остаточная дисперсии:

                 

5) значение критерия Фишера:

 

Значение критерия Фишера сравнивается с критическим для заданного уровня значимости α и числа степеней свободы k—1 и k(n—l).

При неравномерном однофакторном дисперсионном анализе, когда количество наблюдений на уровне А₁ равно n₁, на уровне 

A₂-n₂, .., на уровне А_k—n_k, а общее их число равно 

 

Факторная и остаточная дисперсии находятся по формулам     

        

Остальные операции выполняются так же, как при равномерном анализе.

При двухфакторном дисперсионном анализе сумма квадратов отклонений от общего среднего разделяется на компоненты, отвечающие двум предполагаемым факторам изменчивости  -  А и В. Если по фактору А выделяется р уровней, а по фактору B  -  q уровней, то общее количество групп будет равно m=pq, а исходные данные можно записать в виде таблицы.

Если для каждого сочетания факторов А_iВ_i произведено по n наблюдений,

Оценки средних значений по группам  , по факторам (х_i.. и x_.j.) и общее среднее   в этом случае рассчитываются по формулам

Общая схема вычисления дисперсий при двухфакторном анализе приведена ниже в таблице 3

Проверка гипотезы о влиянии на изменчивость изучаемого свойст­ва каждого фактора в отдельности и их совместного влияния производится по критерию Фишера:

               

Полученные значения F-критерия сравниваются с критическим для заданного уровня значимости и числа степеней свободы, приведен­ного в таблице 3

Таблица 3

Вычисление дисперсий при двухфакторном дисперсионном анализе

Вид дисперсии	Сумма квадратов отклонений	Число степеней свободы	Дисперсия
Факторная по фактору А		p-1
Факторная по фактору В		q-1
Смешанная        по факторам АВ		(p-1)( q-1)
Остаточная		pq(n-1)
Общая		npq-1

При расчете F-критерия в данном случае в знаменателе всегда берется остаточная дисперсия. Поэтому его значение иногда может получиться меньше 1.

Вопрос№17. Анализ однородности геологических совокупностей. Проблемы аномальных значений случайных величин. При использовании одномерных статистических моделей для описания свойств геологических объектов предполагается, что данный объект однороден в отношении изучаемого свойства. Обычно вопрос об однородности решается исходя из принятой геологической модели. Исследуемый объект считается статистически однородным, если он однороден по геологическому строению. Задачи, основанные на проверке гипотезы о статистической однородности геологических объектов, можно разделить на три типа: выделение аномальных значений; разделение неоднородных выборочных совокупностей; оценка степени влияния различных факторов на характер изменчивости свойств геологических объектов. Выявление локальных неоднородностей(аномалий) в строении геологических объектов имеет исключительно важное практическое значение при проведении поисковых работ, так как они часто используются в качестве признаков, указывающих на наличие повышенных концентраций полезных ископаемых. Задача выявления аномальных значений не имеет универсального решения статистическими методами. Аномальное значение должно определятся опытным путем на основе анализа геологических причин изменения значений изучаемых свойств. Статистические характеристики при этом будут иметь вспомогательное значение. В практике геохимических исследований за аномальные значения часто принимают маловероятные значения по абсолютной величине превышающие тройное сигма. Однако этот способ нельзя признать корректным, так как он не гарантирует от ошибок как первого, так и второго рода, причем вероятность этих ошибок оценить нельзя. Если количество наблюдений, принадлежащих разным геологическим совокупностям в неоднородной выборке велико, то возникает необходимость и возможность ее разделения на несколько однородных совокупностей. Простейший способ разделения неоднородных выборочных совокупностей основан на анализе графиков эмпирических кривых распределения.

Вопрос№18. Статистические гипотезы. Критерий Пирсона и другие критерии. Сравнение выборочного распределения с теоретическим. Примеры использования в геологии. После вычисления частот выбранного теоретического распределения необходимо оценить степень согласия между эмпирическими и теоретическими частотами. Для оценки используют критерии лямбда и хи квадрат. Критерий лямбда предложен Колмогоровым и Смирновым. Единственным условием его применения является достаточная численность выборочных данных(несколько десятков). Для сравнения эмпирического распределения с теоретическим критерий лямбда определяют по формуле λ=D/√n, где D – наибольшее значение абсолютной разности между накопленными значениями частот эмпирического и теоретического распределений. Теоретическое значение лямбда не зависит от объема выборки и числа степеней свободы, а определяется только выбранным уровнем значимости. Критерий хи квадрат, предложенный Пирсоном определяют по формуле

σe=√24/n σa=√6/n

Где n эмпирическая частота. Если хи квадрат эмпирическое будет меньше, чем хи квадрат теоретическое гипотеза о согласии эмпирического и теоретического распределения не отвергается. Число степеней свободы определяется в зависимости от применяемого нормального закона f=k-3, k – число интервалов группировки). Условия: 1)Количество интервалов 5-7; 2)количество в интервалах не меньше 5; 3)интервал не должен прерываться. Показатели нормальности распределения Ka<=3, Ke<=3. Ka = A/ σa

Ke=E/ σe.

Вопрос №19. Статистические гипотезы. Проверка гипотез о равенстве дисперсии 2 выборочных совокупностей. Примеры использования в геологии. Сравнение геологических объектов по степени изменчивости, которая оценивается по величине дисперсии или коэффициента вариации тех или иных свойств, необходимо для обоснованного применения принципа аналогии при их изучении. Различие в дисперсиях свойств аналогичных по составу геологических объектов может указывать на различие в истории их формирования и установить однородность изучаемого материала. На сравнении дисперсий основаны также методы определения величин случайных погрешностей различных способов опробования анализов. Если количественные данные о свойствах геологического объекта получены различными способами, то более надежным следует признать тот способ, который дает меньший разброс значений изучаемого свойства, т.е характеризуется меньшей дисперсией. Для проверки гипотезы о равенстве дисперсии обычно используется критерий Фишера. Фишером было установлено, что в случае равенства дисперсий двух нормально распределенных случайных величин, величина F=S1^2/S2^2 при S1^2>S2^2. Распределение по закону Фишера с n1-1 и n2-1 степенями свободы, где n1 – число проб в выборке, по которой получена большая оценка дисперсии S1^2, а n2 – объем второй выборки. Процедура проверки гипотезы сводится к нахождению эмпирического значения F-критерия и сравнению его с табличным значением для принятой доверительной вероятности и степенях свободы k1=n1-1 и k2=n2-1. Если вычисленное значение критерия Фишера превышает табличное, то гипотеза о равенстве двух дисперсий отвергается.

Вопрос №20. Статистические гипотезы. Проверка гипотезы о равенстве средних значений двух эмпирических совокупностей. Примеры использования в геологии.

В палеонтологии статистические методы проверки гипотезы о равенстве средних способствуют объективному разделению семейств ископаемых организмов на виды. Проверка гипо­тезы о равенстве средних содержаний полезного компонента, рассчитанных по рядовым и контрольным пробам, позволяет объективно решить вопрос о наличии или отсутствии система­тических ошибок в результатах рядового опробования. Общим во всех перечисленных случаях является невозможность уверенного решения задач такого типа путем визуального сравнения сред­них значений свойств, так как они характеризуются большой изменчивостью, а объем выборок часто бывает невелик. Как правило, выборочные оценки средних обладают значительными дисперсиями и могут заметно различаться даже для совершен­но аналогичных объектов.

Наиболее часто в геологической практике употребляется па­раметрический критерий Стьюдента t. Его применение основа­но на том, что если из нормально распределенной совокупности отобраны выборки х_1, x₂, ..., х_k объемом в n₁ значений и выбор­ки y₁, y_{2 …..}y_k объемом в n₂ значений, то величина

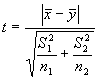
подчиняется закону распределения Стьюдента с n₁+ n₂ - 2 сте­пенями свободы. — выборочные оценки среднего, a , —выборочные оценки дисперсии. Проверка гипотезы о равенстве двух выборочных средних заключается в подстановке в формулу оценок и по первой и и по второй выборке и сравнении полученного значения критерия t с табличным для данного числа степеней свободы и заданной доверительной вероятности. Если расчетное значение критерия превышает табличное, то гипотеза о равенстве выбо­рочных средних отвергается.

Число степеней свободы – число данных изучаемой совокупности, которые могут принимать произвольные значения, не изменяющие общего уровня, около которого это варьирование происходит.

Вопрос №21. Статистические гипотезы о нулевой и альтернативных гипотезах, критерии согласия. Критерии односторонние и двусторонние, параметрические и непараметрические. Примеры использования в геологии. Если задача сводится к проверке гипотезы об отсутствии различия сравниваемых статистик. Такое предположение принято называть нулевой гипотезой и обозначать H0 – Так, для первой ситуации нулевой гипотезой является допущение того, что сомнительное значение принадлежит к той же генеральной совокупности, что и остальные выборочные данные. Для второй ситуации ею является допущение, что изучаемые явления не различаются по средним содержаниям. Нулевая гипотеза должна быть отвергнута в том случае, если ее вероятность мала. На практике она отвергается при P(H0)<α, где α – принятый уровень значимости. В том случае, когда нулевая гипотеза не подтверждается и должна быть отвергнута, Различие сравниваемых статистик признается существенным. Если нулевая гипотеза не отвергается, утверждать, что рассматриваемые статистики действительно равны, нет оснований, хотя это и возможно. Отбор дополнительных данных может привести к тому, что нулевую гипотезу придется отвергнуть. Для гипотезы H0 может существовать несколько альтернативных гипотез H1. Альтернативные гипотезы: 1) Mx больше или меньше верхней границы доверительного интервала. 2) Mx больше верхней или меньше нижней границы доверительного интервала. Для решения задач используются параметрические( Стьюдента, Фишера) и непараметрические( Вилкоксона, Сиджела-Тьюки) критерии согласия, учитывающие свойства выборочных оценок. Параметрические критерии согласия выводятся из свойств известных статистических законов распределения. Для их использования необходимо предварительно проверить гипотезу о соответствии выборочных данных теоретическому закону распределения. Непараметрические критерии могут использоваться даже в том случае, если закон распределения случайных величин неизвестен. Критерий Вилкоксона основан на процедуре ранжирования двух сравниваемых выборок( А и Б) и представляет собой сумму рангов членов меньшей выборки в общем ранжированном ряду из обеих выборок. Если гипотеза о равенстве средних по совокупностям А и Б верна, т.еH0:x1=x2, математическое ожидание статистики Вилкоксона и величины возможных отклонений от нее выборочных оценок зависят только от объемов выборок n1 и n2. Для случаев, когда n1 и n2<25 значения удвоенного математического ожидания критерия Вилкоксона (2MW) и его нижнего критического значения W1 для заданного уровня значимости приведены в специальных таблицах. Верхнее критическое значение критерия W2 определяется из уравнения W2=2MW-W1.

Критерий Сиджела-Тьюки построен исходя из предположения о равенстве центров распределения сравниваемых совокупностей. Поэтому в случае несоблюдения этого условия исходные данные по каждой выборке необходимо центрировать относительно их медиан т.е сравнивать не сами значения изучаемых параметров, а их отклонения от медиан. Значения сравниваемых выборочных совокупностей объединяются в общую выборку и записываются в виде вариационного ряда в порядке их возрастания: x1<x2…<xN-1, где N=n1+n2 – объем общей выборки, n1 – объем меньшей выборки.

Вопрос №22. Двумерные статистические модели. Сущности и условия их применения. Функциональные и корреляционные связи. Основные характеристики двумерного распределения случайных величин. Ковариация, коэффициент корреляции и корреляционное отношение.

В двумерной статистической модели объект исследования рассматривается как двумерная статистическая совокупность, а ее основной характеристикой является двумерная функция рас­пределения случайных величин X и Y.

Основными числовыми характеристиками двумерного рас­пределения случайных величин являются показатели их связи: ковариация, или корреляционный момент, ко­эффициент корреляции и корреляционное отношение.

Ковариация, или корреляционный момент, представляет со­бой математическое ожидание произведения отклонений двух случайных величин от их математических ожиданий

cos (x; у) =М[(х - Мх) (у - My)] = М [( - М ) ( - М )].

Коэффициент корреляции представляет собой ковариацию, нор­мированную по стандартным отклонениям:

Пределами изменения коэффициента корреляции являются р = - 1 и р= + 1, причем значение ±1 соответствует функцио­нальной связи величин, а р —0 полному отсутствию линейной связи. Знак коэффициента ( + ) или (-) указывает на харак­тер связи (прямая или обратная).

Корреляционным отношением называется отношение дис­персий (стандартов) центров условных распределений к общей дисперсии (стандарту) величины. Таких отношений в двумер­ном распределении, может быть два:

Величины корреляционных отношений изменяются в пре­делах от 0 до 1. Значение  = 0 свидетельствует о независимо­сти величин, образующих двумерное распределение.

Вопрос №23. Корреляционный анализ. Понятие и геологические задачи. Корреляционное поле точек, его поле и ориентировка. Линейная и не линейная, прямые и обратные корреляционные связи. Проверка гипотезы о наличии корреляционной связи и ее характере.

Между случайными переменными X и Y существует кор­реляционная зависимость, если каждому значению независи­мой переменной X соответствует некоторое распределение пе­ременной Y, причем с изменением значений Xi закономерно изменяются математические ожидания y_i этих распределений.

Выявление корреляционных связей между различными свойствами геологических объектов способствует решению весьма широкого круга задач (изучении геологических процессов, разработке поисковых критериев и факторов контроля оруденения, а также при выборе рациональных комплексов методов исследований при геологическом картировании, поисках и разведке месторождений).

По тесноте различают связь сильную, среднюю и слабую; по характеру — прямую и обратную; по форме — линейную и нелинейную.

Изучение корреляционных зависимостей проводится таб­личным, графическим и аналитическим методами.

При табличном изучении корреляционных связей зави­симость между величинами X и Y задается двумерной табли­цей, называемой корреляционной решеткой.

Каждому интервалу значений интенсивности магнитного поля соответствует определенное распределение запасов, при­чем с изменением Z распределения Q изменяются в сторону больших значений.

Графическим изображением совокупности всех пар зна­чений (х_i, y_i) является множество точек плоскости, образую­щих поле корреляции.

Наиболее полный метод изучения корреляционных зави­симостей — аналитический, состоящий в установлении число­вых показателей меры и формы зависимости между X и Y. Основные из них — корреляционное отношение и коэффици­ент корреляции.

Выявление корреляционных связей между различными свойствами геологических объектов способствует решению весьма широкого круга задач (изучении геологических процессов, разработке поисковых критериев и факторов контроля оруденения, а также при выборе рациональных комплексов методов исследований при геологическом картировании, поисках и разведке месторождений).

Проверка гипотезы о наличии корреляционной связи обычно основана на том, что для двумерной нормально распределенной случайной величины XY при отсутствии корреляции между Х и У ко­эффициент корреляции и корреляционное отношение равны нулю. 

Проверки заключается в расчете выборочных оценок этих характеристик и оценке значимости их отличия от нуля. Выборочная оценка коэффициента корреляции может быть рассчи­тана по формуле:

 

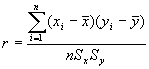
где   и   - выборочные оценки средних значений случайных величин X и У; S_x и S_y - выборочные оценки их стандартов; n - количество сравниваемых пар значений.

Когда математическое ожидание выборочного коэффициента корреляции равно нулю,

 величина  имеет распределение Стьюдента с n - 2 степенями свободы. Если рассчитанное по этой формуле значение величины  превышает табличное значение критерия Стьюдента  для принятой доверительной вероятности и числа степеней свободы n - 2, гипотеза об отсутствии корреляционной связи отвергается.

Вопрос №24. Регрессивный анализ. Уравнение регрессии их расчет и использование в геологии.

Регрессионный анализ - мате­матическое описание выявленной зависимости, дающее воз­можность численно оценивать одни параметры через другие.

Проведение регрессионного анализа можно разде­лить на три этапа: выбор формы зависимости (типа уравнения); вычисление коэффициентов выбранного уравнения; оценка достоверности полученного уравнения.

Регрессионный анализ применяется для:  

— оценки содержания сопутствующих компонентов по содержаниям основных компонентов в рудах.

— определения объемной массы руд.

— интерпретации результатов геофизических методов опробования.

— уточнения оценок параметров рудных тел по результатам отработки.

Решение задач данного типа основано на построении эмпирических линий регрессии или расчете их аналитических выражений—уравнений регрессии. Для правильного решения таких задач необходимо не только оценить силу корреляционной связи, но и выявить ее характер.

Уравнением регрессии Y и X называется уравнение вида y = f(x), устанавливающее зависимость между значениями независимой переменной X и условными средними зависимой переменной Y. По виду различают линейные и нелинейные уравнения связи.

Системе из двух случайных величин всегда будет соответствовать две линии регрессии: y_x=f(x)—регрессия У по X и x_y=f(y)—регрессия Х по У. Если линии регрессии прямые, то регрессия двух величин называется линейной. В более сложных случаях линии регрессии соответствуют кривым линиям, а регрессия случайных величин называется нелинейной.

Для линейной регрессии будем иметь следую­щую пару уравнений:

у=а₁+b₁х (регрессия У по X);

х=а₂+b₂у (регрессия Х по У).

В общем случае прямые регрессии пересекаются в точке, координа­ты которой равны математическим ожиданиям величин Х и У, а угол γ между ними изменяется от 0 до 90°. Чем меньше угол γ , тем сильнее связь между величинами. Степень связи между величинами зависит от того, какая величина взята в качестве аргумента, а для полной характеристики связи всегда необходимо знать оба коэффициента регрессии. Если угол γ =0 и обе линии регрессии сливаются в одну прямую, то  , а связь между величинами становится функциональной.

Вопрос №25. Ранговый коэффициент корреляции и его использование в геологии. Использование корреляционных связей для предсказания свойств геологических объектов.

Расчет рангового коэффициента корреляции основан на замене выборочных значений исследуемых случайных величин их рангами в порядке возрастания. При этом предполагается, что если между значениями случайных величин нет корреляционной зависимости, то ранги этих вели­чин тоже будут независимыми. Выражение для расчета ранго­вого коэффициента корреляции имеет вид

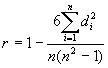
Где d_i - разность рангов сопряженных значении изучаемых ве­личин x_i И y_i

п — количество пар в выборке.

Если для двух величин на основании представительной выборки доказано наличие корреляционной связи, определен ее вид и подобрано описывающее его уравнение, то создается возможность прогноза значений одной из случайных величин по значениям другой.

Для изучения связей между такими величинами используются методы регрессионного анализа, позволяющие установить влияние произвольно выбранных значений одной величины (например, X) на значения другой, нормально распределенной случайной величины (например, У). В отличие от корреляционного анализа в этом случае анализиру­ются только регрессии У и X, но не наоборот.