vector

Утверждение 2. Если вектор а задан двумя точками: началом в точке

M (xM , yM , zM ) и концом в точке N (xN , yN , zN ) , т.е. a MN (рис. 12), то его

декартовы координаты ax , ay , az находятся по формулам:

ax xN xM ,

ay yN yM ,

(10)

az zN zM .

Модуль вектора а вычисляется по формуле:

		z
			A(xA, yA, zA)
		k
			j
х	i	О	у

| a | a2	a2	a2 .		(11)
x	y	z
Определение.			Косинусы	углов
, , , которые вектор образует с осями
координат		(cos , cos , cos ) , называются
направляющими косинусами этого				вектора
(рис. 11).

Они представляют собой компоненты единичного вектора и связаны соотношением:

Рис. 11.	cos2 cos2 cos2 1.	(12)
Координаты вектора связаны с его направляющими косинусами
следующим образом:
	ax | a | cos ,
	ay | a | cos ,	(13)
	az | a | cos .
Замечание 2.	Соотношения (11)-(13) справедливы только	в

прямоугольной декартовой системе координат.

31

z

az

N(xN, yN, zN)

a

	k		M(xM, yM, zM)	ay
		j
i	О			у

aх

х

Рис. 12.
ПРИМЕР 2.4.1. Даны точки	A(1, 2, 0),	B( 2, 3, 1) , вектор

a {0, 1, 2}. Найти:

а) координаты вектора AB и противоположного вектора;

б) модули векторов AB и BA;

в) направляющие косинусы вектора AB ;

г) координаты точки С, с которой совпадает конец вектора а, если его начало совпадает с точкой В.

Решение. а) Начало вектора b AB совпадает с точкой А, конец – с

точкой В. Используя формулы (10), находим координаты bx , by , bz вектора

AB :

32

bx xB xA 2 1 3, by yB yA 3 ( 2) 5, bz zB zA 1 0 1.

Следовательно, AB { 3, 5, 1}, тогда противоположный вектор BA имеет координаты BA {3, 5, 1}.

б) Применяя формулу (11), получим:

| AB | ( 3)2 52 ( 1)2 35 | BA | .

в) Направляющие косинусы вектора AB находим из формул (13):

3

,

3

35 cos

cos

35

5

5

35 cos

cos

,

35

1

.

1

35 cos

cos

35

г) Имеем a BC . Обозначая координаты точки С через xC , yC , zC , с

помощью формул (10) получим уравнения:

0 xC ( 2),

1 yC 3,

2 zC ( 1).

Откуда xC 2,

yC 4,

zC 1 и, следовательно, C( 2,

4, 1) .■

ПРИМЕР 2.4.2. Может ли вектор составлять с координатными осями

углы: а) 45 ,

135 , 60 ;

б) 150 ,

30 ?

Решение. а) Проверяем, выполняется ли соотношение (12):

cos2 45 cos2 135 cos2 60

				2						2		1 2
	2						2								1		1		1		1
																				1		1.
	2						2					2			2		2		4		4

Ответ: не может.

б) Поскольку угол γ не задан, попытаемся найти его из соотношения (12):

cos2 150 cos2 30 cos2 1,

33

					2					2
		3					3				cos2 1,
		2					2

	3		3	cos2 1	cos2						1	.
4			4						2
Ответ: не может.■
ПРИМЕР 2.4.3. Дан модуль вектора | a | 3													и углы, которые этот вектор
составляет с осями координат 45 ,										60 ,			120 . Найти проекции
вектора а на координатные оси.
Решение. Отмечая, что					cos2 45 cos2 60 cos2 120 1, искомые
проекции ax , ay , az находим по формулам (13):
ax | a | cos 3cos 45						3			2	,
						2
ay | a | cos 3cos 60							3	,
						2

az | a | cos 3cos120 32 . ■

ПРИМЕР 2.4.4. Определить координаты точки М и координаты ее радиус-вектора, если последний составляет с координатными осями

одинаковые углы и его модуль равен 53 .

Решение. Т.к. , то соотношение (12) приводит к уравнению cos2 cos2 cos2 1,

разрешая которое относительно cos , получим cos2 13 cos 13 .

Координаты точки M (xM , yM , zM ) совпадают с координатами ее радиус-

вектора, т.е. вектора OM {xM , yM , zM }. Т.к. получено два значения cos ,

то по формулам (13) имеем два радиус-вектора OM1, OM 2 и две точки М1 и

М2:

34

								1
xM1	yM1	zM1	5	3								5					M1(5, 5, 5),	OM 1 {5, 5, 5};
								3
												1
xM 2	yM 2	zM 2	5 3														5
												3

			M2 ( 5, 5, 5),		OM 2		{ 5, 5, 5}. ■
ПРИМЕР 2.4.5. По данным векторам				а, b	и	с	(рис.13) построить
векторы:
а) a b;	б) a b ;	в) a b ;	г) a b c ;	д) a / 2 ;		е) 2b ; ж) 2b a / 2.

	b	c
а

Рис. 13.

Решение. а, б) В произвольной точке А (рис.14) строим вектор, равный вектору а, и вектор, равный вектору b, после чего на этих двух векторах, как на сторонах, строим параллелограмм АBCD. Тогда по правилу параллелограмма

его направленная диагональ,				выходящая из точки А,					будет	вектором
AC a b ,	а вторая диагональ этого параллелограмма							с	направлением от
конца вектора b (точка В) в				конец	вектора	а	(точка	D), будет		вектором
BD a b .
			B		а + b	C
				b			а – b
	K			A	а		D
		– а – b
				Рис. 14.
в) По	свойству			линейных		операций			над	векторами
a b (a b) AC CA,				т.е. у	вектора		AC a b		надо	изменить

направление или в точке А построить вектор AK CA (рис. 14).

г) Строим вектор a b c по правилу треугольника, используя свойство

 линейных операций: a b c (a b) c AC c (рис. 15а). От конца уже

35

построенного вектора a b (точка С) откладываем вектор CE , равный вектору

с, и соединяем начало первого (точка А) с концом последнего (точка Е),

получаем вектор AE a b c .
		C				H
A			A		а	с	b
		с					G
а + b + с		Е	а + b + с			Е
	Рис. 15а.			Рис. 15б.
Иначе: можно в произвольной точке А построить вектор							AG ,	равный
вектору а (рис. 15б), от его конца (точка G) отложить вектор							GH ,	равный

вектору b, от конца последнего (точка Н) отложить вектор HE , равный вектору

с, и, наконец, соединить начало первого вектора (точка А) с концом последнего

(точка Е) и получить вектор AE a b c .

	М	L	2b
			B
	2b – а/2		b
			F – а/2 A	а		D
			Рис. 16.
д) Рис. 16: на продолжении вектора AD a					откладываем отрезок AF,
длина которого в два раза меньше длины отрезка AD. Получаем вектор									AF с
направлением, противоположным вектору а (согласно определению λ а).
е) Рис. 16: продолжаем вектор AB за точку В на длину вектора									AB ,
получаем вектор AL 2b .
ж) Рис. 16: т.к.		2b a / 2 2b ( a / 2) AL AF ,				то	по	правилу
параллелограмма, построенного на векторах				AL	и AF ,	как	на	сторонах,

диагональ, выходящая из точки А в направлении точки М, будет искомым вектором AM 2b a / 2 . ■

36

ПРИМЕР 2.4.6. Доказать, что при любом расположении точек А, В и С

справедлива формула AB BC CA 0.

Решение. Как бы ни были расположены точки А, В и С (на рис. 17

показаны три из возможных вариантов), складывая векторы по правилу треугольника, имеем: от конца вектора AB (точка В) откладываем вектор BC ,

затем от конца вектора BC (точка С) откладываем вектор CA, начало результирующего вектора совпадает с началом первого из векторов-слагаемых,

т.е. с точкой А, а конец – с концом последнего из векторов-слагаемых, т.е. с той же точкой А. Таким образом, у результирующего вектора начало совпадает с концом, это и есть нуль-вектор 0 . Справедливость формулы доказана. ■

		CA
В
A	С A	В	С
	AB		BC
CA	С	BC
A			В
	AB
	Рис. 17.
ПРИМЕР 2.4.7. Показать, что		| a b |	| a | | b | . При каком

условии на векторы а и b имеет место знак равенства?

Решение. Если векторы а и b не коллинеарны, то три вектора а, b и

а + b образуют треугольник (рис. 18а), в котором длина одной стороны | a b |

меньше суммы длин двух других сторон | a | | b | по неравенству треугольника.

37

а

b

а

а

b

b

а + b

а + b

а + b

Рис. 18а.

Рис. 18б.

Рис. 18в.

Если

векторы

а

и b

коллинеарны и

одинаково

направлены,

то

| a b | | a | | b | (рис. 18б).

Если векторы а и b коллинеарны и направлены противоположно,

то

| a b |

| a | | b |

(рис. 18в).■

ПРИМЕР 2.4.8. Векторы

а и b образуют

угол

120º,

| a | 3,

| b | 5 .

Вычислить | a b | и | a b | .

Решение. На

рис.

19 изображены

а + b

C

А

а – b

вектор

a OA

и

b OB .

Согласно

правилу

параллелограмма, векторы а + b

а 120º

и

а – b

являются

диагоналями

О

b

60º

В

параллелограмма ОАСВ (рис. 19).

Рис. 19.

Применим теорему косинусов к треугольнику ОАВ:

| a b |2 | a |2

| b |2

2 | a | | b | cos

( AOB)

или

| a b |2 32 52 2 3 5 cos120 9 25 30 ( 1/ 2) 49 ,

следовательно, | a b | 7 .

Применяя ту же теорему в треугольнике ОСВ, получим:

| a b |2 | a |2 | b |2 2 | a | | b | cos

( OBC)

или

| a b |2 32 52 2 3 5 cos 60 9 25 30 (1/ 2) 19,

и тогда | a b | 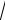19 . ■

38

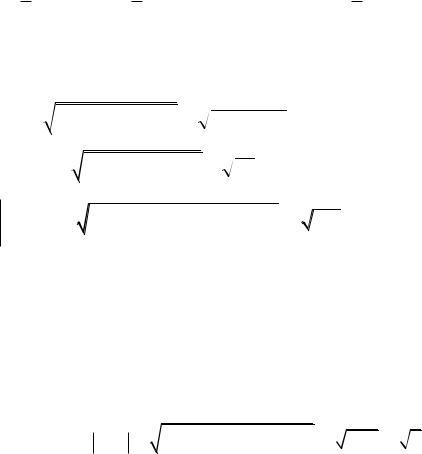
ПРИМЕР 2.4.9. Даны векторы a {3, 2, 6},

b { 2, 1,

0}.

а) Найти векторы 1) a b ;

2)

a b ;

3) 2a ;

4)

b

;

5)

b

2a .

2

2

б) Вычислить | a | , | a b | и

b

2a

.

2

в) Найти направляющие косинусы векторов а и b / 2.

Решение. а) По формуле (5) находим

1) a b {3 2, 2 1,

6 0} {1, 1, 6}.

По формуле (6) получаем b {2, 1, 0}, тогда по формуле (5)

2) a b a ( b) {3 2, 2 1, 6 0} {5, 3,

6}.

По формуле (6)

3)2a 2 {3, 2, 6} { 6, 4, 12}.

4)b / 2 { 2 / 2, 1/ 2, 0 / 2} { 1, 1/ 2, 0}.

По формуле (5), используя результаты 3), 4), имеем

5) b2 2a { 1, 12 , 0} { 6, 4, 12} { 7, 92 , 12}.

б) Воспользовавшись результатом 1), 5) пункта а), по формуле (11)

находим

| a | 32 ( 2)2 62 9 4 36 7 ,

| a b | 12 ( 1)2 62 38 ,

	b
				( 7)2 (9 / 2)2 ( 12)2
		2a			853 / 2 .
	2

в) С использованием результата б) по формулам (13) для вектора а имеем

3 7 cos		cos 3 / 7,
2 7 cos		cos 2 / 7,
6 7 cos		cos 6 / 7.

Чтобы воспользоваться теми же формулами для вектора b / 2, надо сначала

вычислить его модуль: b / 2 ( 1)2 (1/ 2)2 02 5 / 4 5 / 2 . Тогда

39

								5
	1													cos		cos 2 / 5,
							2
		1						5					cos			cos 1/
																	5,
	2						2
	0									5		cos				cos 0. ■
							2
ПРИМЕР 2.4.10. Даны																проекции	силы F на координатные оси:
F {4,	4, 4 2}. Найти величину силы F и направление ее действия.

Решение. Величина силы F есть

| F | 42 42 ( 42)2 16 16 32 8.

Направление вектора задают его направляющие косинусы, которые

определим по формулам (13):
	4 8cos ,	4 8cos ,	4 2 8cos .
Откуда	cos 1/ 2,	cos 1/ 2 ,	cos 2 / 2.

Следовательно, вектор силы F образует с координатными осями Ох, Оу, Оz

углы 60 , 60 , 135 соответственно. ■

ПРИМЕР 2.4.11. Проверить коллинеарность векторов a {2, 6, 8} и b { 1, 3, 4}. Установить, какой из них длиннее другого и во сколько раз, как

они направлены – в одну или в противоположные стороны.

Решение. Проверяем условие коллинеарности (8):

2 6 8 2 ,

1 3 4

следовательно, векторы а и b коллинеарны, причем a 2b , значит, вектор а длиннее вектора b в два раза, направлены эти векторы противоположно

( 2 0 ). ■

40