2. Решение задачи структурной идентификации модели предсказания давления насыщенного пара индивидуального вещества

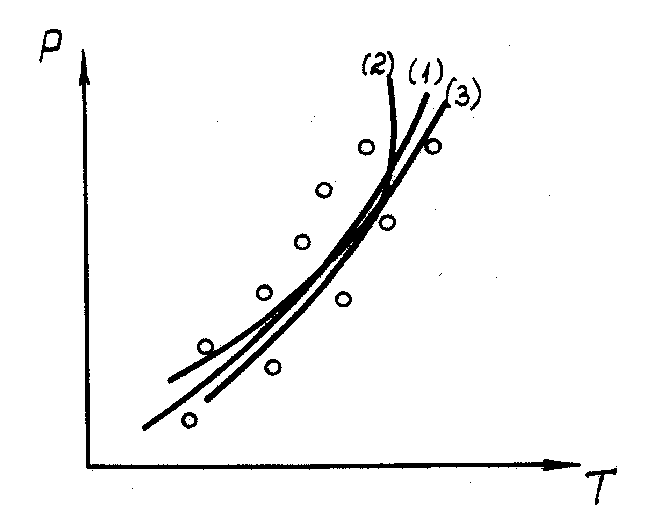
Экспериментальные данные зависимости давления насыщенного пара индивидуального вещества от температуры представлены в табл. 1 и на графике 1 (кружочки):

Таблица 1.

Экспериментальные данные

№	Т	Р
1	Т1	Р1
2	Т2	Р2
.	..	…
n	Tn	Pn

Рис.1. Схематическое представление

сравнений экспериментальных (о) и

расчетных ( ) данных

Для описания приведенной экспериментальной зависимости предлагается использовать 3 модели [7]:

- 2-х коэффициентное уравнение Кирхгофа (p=2):

(6)

3-х коэффициентное уравнение Антуана (p=3):

(7)

4-х коэффициентное уравнение Риделя (p=4):

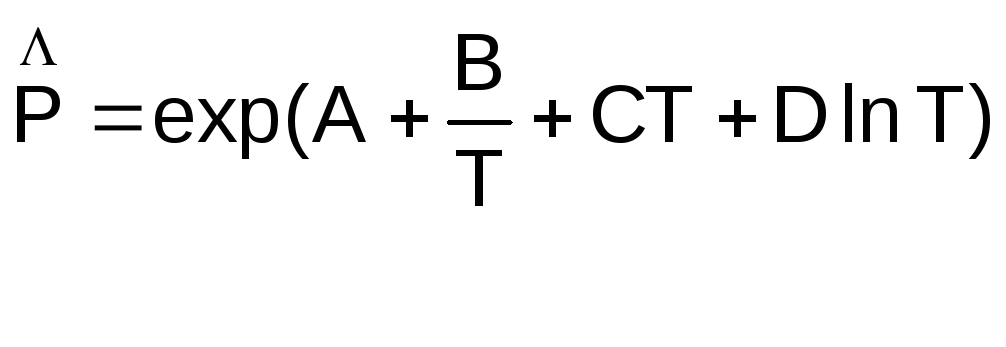(8)

Задача структурной идентификации заключается в выборе уравнения, наилучшим образом описывающего экспериментальные данные. Перед тем, как сравнивать эти при уравнения, для каждого из них должна быть решена задача параметрической идентификации и определены соответствующие коэффициенты А, В, С, D. После этого графики зависимостей (6), (7) и (8) могут быть представлены на рис.1.

В данном случае в качестве количественного критерия выбора уравнения (решения задачи структурной идентификации) предлагается использовать остаточную дисперсию [6]:

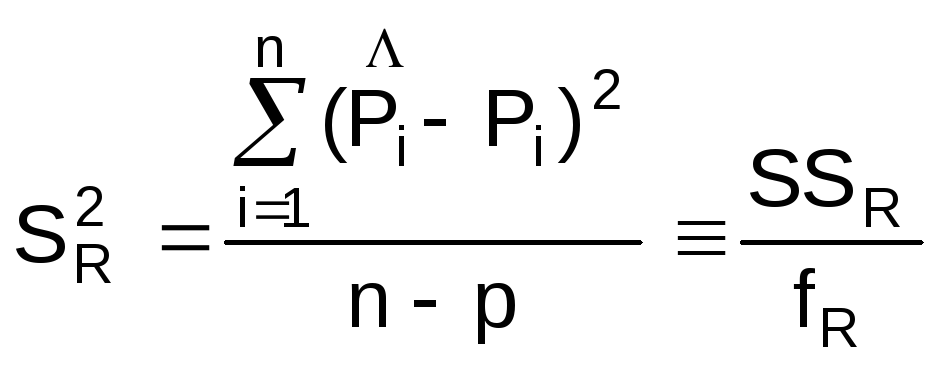(9)

Числитель этого выражения SS_R представляет собой сумму квадратов остаточной дисперсии, а знаменатель f_R – число степеней свободы остаточной дисперсии (р – число коэффициентов уравнений: либо 2,3 или 4).

Предлагается выбрать то уравнение, для которого остаточная дисперсия будет наименьшей.

Выбранное уравнение наилучшим образом описывает экспериментальные данные и его можно рассматривать как результат решения задачи структурной идентификации.

3. Решение задачи параметрической идентификации модели предсказания давления насыщенного пара индивидуального вещества

В общем случае при решении задачи параметрической идентификации – определении (подгонке) параметров-коэффициентов моделей предъявляются два основных требования:

- они должны обладать интерполяционными возможностями, т.е. по известным (экспериментальным) дискретным значениям выходных переменных , в т.н. узловых точках можно правильно вычислять значения(2) между узловыми точками;

- они должны обладать экстраполяционными возможностями, т.е. способностью правильно определять значения выходных переменных (2) за пределами отрезка узловых точек, где был проведен эксперимент.

Для решения задач интерполяции в свое время был предложен одноименный метод – метод интерполяции, в котором предполагается приравнивание рассчитанных значений выходных переменных , зависящих от искомых параметров-коэффициентов(2), к экспериментальным значениям. В этом случае полученная система уравнений решается относительно искомых коэффициентов(2)[8].

Для решаемой задачи параметрической идентификации метод интерполяции предполагает решение системы нелинейных уравнений:

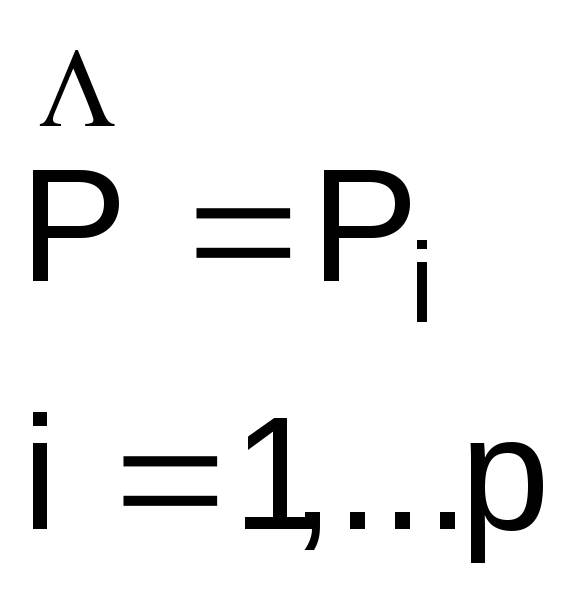(10)

и с учетом, например, уравнения (3)

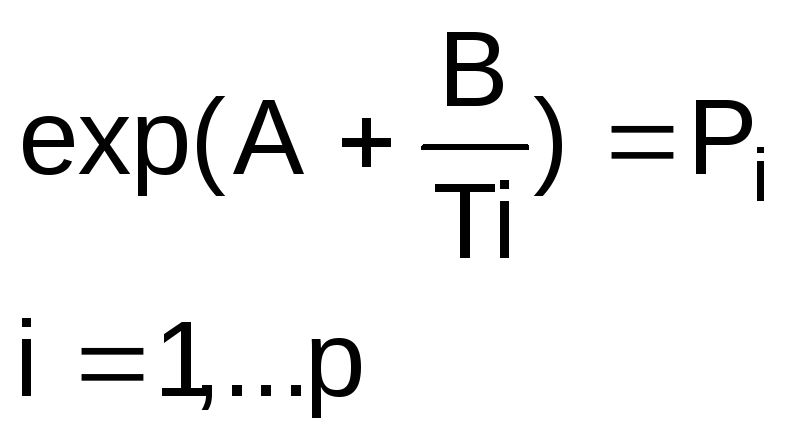(11)

Последнюю систему уравнений можно линеаризовать при логарифмировании, в результате чего получается система 2-х линейных алгебраических уравнений относительно параметров А и В следующего вида:

(12)

Значения Т и Р в этой системе берутся из таблицы экспериментальных данных 1.

Характерной особенностью метода интерполяции является то обстоятельство, что число экспериментальных значений, используемых при решении соответствующей системы уравнений (11) или (12), точно равно числу определяемых параметров р, т.е. количество экспериментальных измерений ограничено. Это относится к недостаткам метода интерполяции, т.к. не понятно, какие экспериментальные данные использовать для вычислений и что делать с "лишними" данными. Также нельзя признать обоснованным равенство расчетных и экспериментальных значений выходных переменных модели, т.к. опытные данные не являются точными.

Поэтому обычно метод интерполяции применяется описания поведения объектов многочленами и исключительно в пределах отрезка узловых точек, где был проведен эксперимент, т.е. не для экстраполяции.

Для решения задач одновременно интерполяции и экстраполяции используется метод аппроксимации, в котором используются все экспериментальные данные (нет "лишних" данных) и определяются такие значения параметров-коэффициентов, чтобы модель (уравнения) наиболее точно описывала и приближалась к экспериментальным точкам, но не совпадала с ними.

Можно использовать три различных критерия для оценки степени близости расчетных и экспериментальных значений выходной переменной (2):

- критерий метода наименьших модулей:

(13)

- критерий метода наименьших квадратов (МНК)

(14)

- критерий "минимаксного" метода Чебышева:

(15)

1in

При определении коэффициентов методом аппроксимации стремятся к тому, чтобы эти критерии принимали в результате решения задачи наименьшие значения (отсюда и название методов, например, МНК).

Наибольшее распространение получил метод наименьших квадратов –МНК, которому соответствует критерий (14).

При более строгой записи этого критерия он включает весовой коэффициент _i:

(16)

Весовой коэффициент может задаваться двумя способами:

- эмпирически, когда он характеризует большую и меньшую точность описания конкретной точки измерения i;

- c учетом дисперсии измерения, когда его приравнивают величине обратной дисперсии измерения, т.е. , что означает стремление более точному описанию опытных данных с меньшими ошибками.