Тема ¹4. Автоматы

Содержание

Автоматы	2
Изоморфизм и эквивалентность автоматов	7
Минимизация автоматов	10
Частичные автоматы и их минимизация	13
Распознавание множеств автоматами	18
Автоматы Мура . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .	18
Программная реализация логических функций и автоматов	19
Предметный указатель	24

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Автоматы

Конечным автоматом называется система S = {A, Q, V, δ, λ}, в которой A = {a1, . . . , am}, Q =

{q1, . . . , qn}, V = {v1, . . . , vk} — конечные множества (алфавиты), а δ : Q × A → Q и λ : Q × A → V — функции, определенные на этих множествах.

A — входной алфавит, V — выходной алфавит, Q — алфавит состояний, δ — функция переходов, λ — функция выходов. Если, кроме того, в автомате S выделено одно состояние, называемое начальным (обычно будет считаться что это q1), то полученный автомат называется инициальным и обозначается (S, q); т.о., по неинициальному автомату с n состояниями можно n различными способами определить инициальный автомат. Поскольку функции δ и λ определены на конечных множествах, их можно задавать таблицами. Обычно две таблицы сводятся в одну таблицу δ × λ : Q × A → Q × V , называемую таблицей переходов автомата или просто автоматной таблицей.

Пример 1. Таблица задает функции переходов и выходов для автомата с алфавитами A = {a1, a2, a3},

Q = {q1, q2, q3, q4}, V = {v1, v2}.

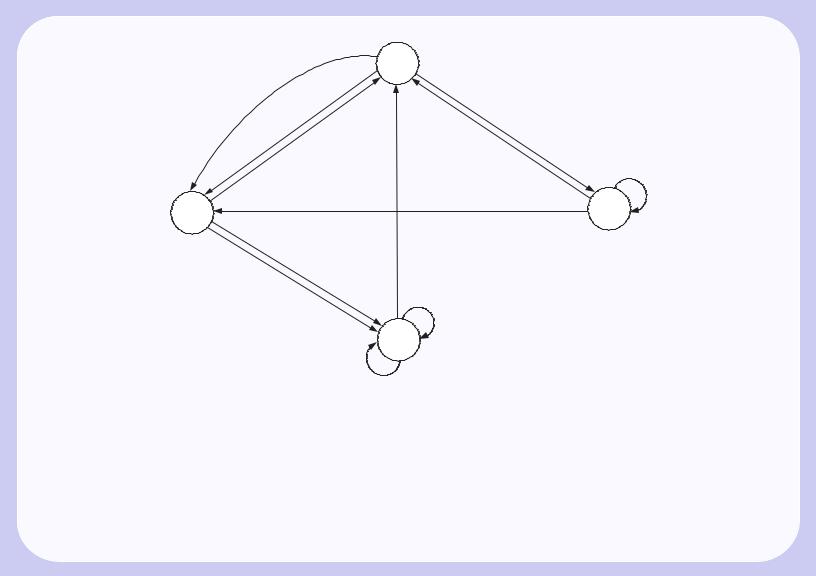
Еще один распространенный и наглядный способ задания автомата — ориентированный мультиграф, названный графом переходов или диаграммой переходов. Вершины графа соответствуют состояниям; если δ (qi, aj) = qk и λ(qi, aj) = vi, то из qi в qk ведет ребро, на котором написано aj и vi.

	a1	a2	a3
q1	q3, v1	q3, v2	q2, v1
q2	q4, v1	q1, v1	q1, v1
q3	q2, v1	q3, v1	q3, v2
q4	q4, v1	q2, v1	q1, v2

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

|v 1 a 3

	v 1
|
a 2	v 1
	|
	a 3

q 1

	a	|
	2
		v
a		2
	|
1
	v
	1

q 2

		a	|
		1
			v
1	a		1
v	2	|
|		v
		1
1
a
	a3 | v2

a2 | v1

q 4

a1 | v1

q 3

a3 | v2

Кратные ребра не обязательны; например, два ребра из q2 в q1 можно заменить одним, на котором будут написаны обе пары q3v1 и q2v1. Для любого графа переходов в каждой вершине qi выполнены следующие условия, которые называются условиями автоматности или корректности:

1.для любой входной буквы aj имеется ребро, выходящее из qi, на котором написано aj (условие полноты);

2.любая буква aj встречается только на одном ребре, выходящем из qi (условие непротиворечиво-

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

сти или детерминированности).

Для данного автомата S его функции δS и λS могут быть определены не только на множестве A всех входных букв, но и на множестве A всех входных слов. Для любого входного слова α = aj1aj2 . . . ajk

δ(qi, aj1, aj2, . . . , ajk) = δ(δ(. . . δ(δ(qi, aj1), aj2), . . . , ajk−1), ajk).

Это традиционное определение «с многоточиями»; намного точнее и лучше читается индуктивное определение:

а) δ(qi, aj) задается автоматной таблицей S;

б) для любого слова α A и любой буквы из ajδ(qi, αaj) = δ(δ(qi, α), aj).

С помощью расширенной функции δ определяется расширенная функция λ:

λ(qi, αaj) = λ(δ(qi, α), aj).

Зафиксируем в автомате S начальное состояние q1 и каждому входному слову α = aj1aj2 . . . ajk поставим в соответствие слово ω в выходном алфавите:

ω = λ(q1, aj1)λ(q1, aj1aj2) . . . λ(q1, aj1 . . . ajk).

Это соответствие, отображающее входные слова в выходные, называется автоматным отображением, а также автоматным оператором, реализуемым автоматом (S, q1). Если результатом применения оператора к слову α является выходное слово ω, то это будем обозначать соответственно S(q1, α) = ω или S(α) = ω.

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Число букв в слове α называется длиной α и обозначается |α| или l(α). Автоматное отображение также удобно определять индуктивно:

S(qi, aj) = λ(qi, aj)

S(qi, αaj) = S(qi, α)λ(δ(qi, α), aj)

Автоматное отображение обладает двумя свойствами:

1.слова α и ω = S(α) имеют одинаковую длину: |α| = |ω| (свойство сохранения длины);

2.если α = α1α2 и S(α1α2) = ω1ω2, где |α1| = |ω1|, то S(α1) = ω1; иначе говоря, образ отрезка длины l равен отрезку образа той же длины.

Свойство 2 отражает тот факт, что автоматные операторы — это операторы без предвосхищения, то есть операторы, которые, перерабатывая слово слева направо, «не заглядывают вперед»: i-ая буква выходного слова зависит только от первых i-букв выходного слова. Пример оператора с предвосхищением — оператор, который слову α = ai1 . . . aik ставит в соответствие его отражение, то есть слово aik . . . ai1; первая буква выходного слова равна здесь последней букве входного слова.

Введенные определения наглядно интерпретируются на графе переходов. Если зафиксирована вершина qi, то всякое слово α = ai1 . . . aik однозначно определяет путь длины k из этой вершины (обозначим его (qi, α)), на k ребрах которого написаны соответственно буквы ai1, . . . , aik. Поэтому δ(qi, α) — это последняя вершина пути (qi, α), λ(qi, α) — выходная буква, написанная на последнем ребре пути (qi, α), а отображение S(qi, α) — слово, образованное k выходными буквами, на k ребрах этого пути.

Пример 2. Для автомата S из примера 1

δ(q2, a3a2) = δ(q2, a3a1) = q3; δ(q2, a3a1a1) = q2; λ(q2, a3a2) = v2; λ(q2, a3a1) = v1; λ(q2, a3a1a1) = v1.

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель

Заметим, что δ(q2, a3a1) = δ(q2, a3a2), но λ(q2, a3a1) 6= λ(q2, a3a2).

Далее S(q2, a3a2) = v1v2; S(q2, a3a2a1) = v1v2v1, что иллюстрирует свойство 2 автоматного отображения.

Состояние qj называется достижимым из состояния qi, если существует входное слово α такое, что δ(q1, α) = qj. Автомат S называется сильно связным, если из любого его состояния достижимо любое другое состояние.

Автомат называется автономным, если его входной алфавит состоит из одной буквы: A = {a}. Все входные слова автономного автомата имеют вид aa . . . a.

Теорема. Любое достаточно длинное выходное слово автономного автомата с n состояниями является периодическим (возможно с предпериодом), причем длины периода и предпериода не превосходят n; иначе говоря, оно имеет вид δωω . . . ωω1, где ω1 — начальный отрезок ω, при этом 0 6 |δ| 6 n; 1 6 |ω| 6 n.

Действительно, так как в графе автономного автомата A из каждой вершины выходит только одно ребро, то его сильно связные подграфы могут быть только простыми циклами, из которых нет выходящих ребер. Поэтому в компоненте связности может быть только один цикл; остальные подграфы компоненты — это деревья, подвешенные к циклу и ориентированные в его сторону.

Пример 3. Граф автомата, заданный таблицей, имеет вид:

q	1	2	3	4	5	6	7	8	9
a	3,0	4,0	4,0	7,0	4,2	5,0	6,1	9,0	9,1

(входные буквы на ребрах опущены; выходной алфавит V = {0, 1, 2}).

•Назад •Первая •Предыдущая •Следующая •Последняя •Перейти •Предметный указатель