- •Часть 1 введение Лекция 1
- •Основные понятия теории вероятностей
- •Часть 2
- •Лекция 3
- •Условная вероятность и независимость событий.
- •Формула полной вероятности
- •И теорема Байеса
- •Часть 3
- •Последовательность независимых испытаний
- •Лекция 4
- •Независимые испытания. Формула бернулли. Асимптотические формулы муавра – ЛаплАса и пуассона
- •Часть 4 случайные величины Лекция 5
- •Случайные величины. Законы распределения случайных величин
- •Закон распределения. Ряд распределения
- •Дискретной случайной величины
- •Лекция 6
- •Числовые характеристики
- •Случайных величин
- •Лекция 7
- •Распределения дискретных случайных величин
- •Лекция 8
- •Распределения непрерывных случайных величин
- •Часть 5
- •Лекция 10
- •Числовые характеристики системы двух случайных величин. -мерный случайный вектор
- •Часть 6 функции случайных величин Лекция 11
- •Закон распределения и числовые характеристики функций случайных величин
- •Лекция 12
- •Характеристическая функция
- •Часть 7 предельные теоремы теории вероятностей Лекция 13
- •Закон больших чисел и центральная предельНаЯ теорема
- •Часть 8 математическая статистика Лекция 14
- •Основные понятия и задачи математической статистики
- •Лекция 15
- •Статистическое оценивание параметров распределения
- •Лекция 16
- •Проверка статистических гипотез
Лекция 16
Проверка статистических гипотез
ЦЕЛЬ
ЛЕКЦИИ: определить понятие статистических
гипотез и правила их проверки; провести
проверку гипотез о равенстве средних
значений и дисперсий нормально
распределенной случайной величины,
сформулировать критерий согласия
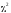 .
.
Определение статистической гипотезы
Статистическойназывается гипотеза о предполагаемом
виде неизвестного распределения или
утверждение относительно значений
одного или нескольких параметров
известного распределения. Например,
совокупность наблюдаемых значений
распределена по закону Пуассона,
математическое ожидание случайной
величины равно
равно – статистические гипотезы.
– статистические гипотезы.
Гипотеза,
которая подвергается проверке, называется
нулевойи
обозначается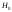 .Альтернативнойгипотезой
.Альтернативнойгипотезой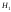 называется гипотеза, конкурирующая с
нулевой, т. е. ей противоречащая. Простой
называется гипотеза, содержащая только
одно предположение. Сложная гипотеза
состоит из конечного или бесконечного
числа простых гипотез.
называется гипотеза, конкурирующая с
нулевой, т. е. ей противоречащая. Простой
называется гипотеза, содержащая только
одно предположение. Сложная гипотеза
состоит из конечного или бесконечного
числа простых гипотез.
Пример.
Пусть проверяется гипотеза о равенстве
некоторого параметра значению
значению ,
т. е. гипотеза
,
т. е. гипотеза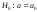 .
В этом случае альтернативной гипотезой
можно рассматривать одну из следующих
гипотез:
.
В этом случае альтернативной гипотезой
можно рассматривать одну из следующих
гипотез: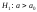 ;
;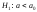 ;
;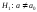 ;
;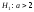 .
Все приведенные гипотезы простые, и
только
.
Все приведенные гипотезы простые, и
только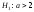 – сложная гипотеза.
– сложная гипотеза.
Выбор альтернативной гипотезы определяется формулировкой решаемой задачи. Причина выделения нулевой гипотезы состоит в том, что чаще всего такие гипотезы рассматриваются как утверждения, которые более ценны, если они опровергаются. Это основано на общем принципе, в соответствии с которым теория должна быть отвергнута, если есть противоречащий ей факт, но не обязательно должна быть принята, если противоречащих ей фактов на текущий момент нет.
Правило,
по которому выносится решение принять
или отклонить гипотезу
 ,
называетсястатистическим
критерием. Проверка статистических
гипотез осуществляется по результатам
наблюдений (экспериментов, опытов), из
которых формируют функцию результатов
наблюдений, называемуюпроверочной
статистикой. Таким образом, статистический
критерий устанавливает, при каких
значениях этой статистики проверяемая
гипотеза принимается, а при каких она
отвергается.
,
называетсястатистическим
критерием. Проверка статистических
гипотез осуществляется по результатам
наблюдений (экспериментов, опытов), из
которых формируют функцию результатов
наблюдений, называемуюпроверочной
статистикой. Таким образом, статистический
критерий устанавливает, при каких
значениях этой статистики проверяемая
гипотеза принимается, а при каких она
отвергается.
Пусть
по
 независимым наблюдениям случайной
величины
независимым наблюдениям случайной
величины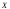 получена некоторая оценка
получена некоторая оценка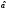 .
Предположим, что есть основания считать
истинное значение оцениваемого параметра
.
Предположим, что есть основания считать
истинное значение оцениваемого параметра равным некоторой величине
равным некоторой величине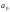 .
Однако даже если истинное значение
параметра
.
Однако даже если истинное значение
параметра и равно
и равно ,
то оценка
,
то оценка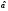 ,
скорее всего, не будет в точности
равняться
,
скорее всего, не будет в точности
равняться из-за статистической изменчивости,
присущей
из-за статистической изменчивости,
присущей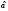 .
Поэтому возникает вопрос. Если
предположить, что
.
Поэтому возникает вопрос. Если
предположить, что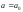 ,
то при каком отклонении
,
то при каком отклонении от
от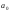 это предположение (гипотеза) должно
быть опровергнуто как несостоятельное?
Ответ на этот вопрос можно получить,
вычислив вероятность любого значимого
отклонения
это предположение (гипотеза) должно
быть опровергнуто как несостоятельное?
Ответ на этот вопрос можно получить,
вычислив вероятность любого значимого
отклонения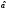 от
от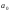 ,
используя закон распределения случайной
величины
,
используя закон распределения случайной
величины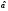 .
.
Если
вероятность превышения разности
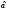 и заданного уровня
и заданного уровня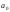 мала, то этот уровень следует считать
значимым и гипотезу
мала, то этот уровень следует считать
значимым и гипотезу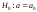 следует отвергнуть. Если вероятность
превышения данной разности не является
малой, то наличие этой разности можно
отнести за счет обычной статистической
изменчивости и гипотезу
следует отвергнуть. Если вероятность
превышения данной разности не является
малой, то наличие этой разности можно
отнести за счет обычной статистической
изменчивости и гипотезу можно считать правдоподобной. Природа
статистических выводов такова, что при
отклонении гипотезы можно заранее
оценить вероятность возможной ошибки
(отклонения истинной гипотезы); напротив,
если гипотеза принята, то это не означает,
что она подтверждена с заданной
вероятностью. Это лишь означает, что
гипотеза согласуется с опытными данными,
но возможно, что для другого эксперимента
гипотеза будет отвергнута.
можно считать правдоподобной. Природа
статистических выводов такова, что при
отклонении гипотезы можно заранее
оценить вероятность возможной ошибки
(отклонения истинной гипотезы); напротив,
если гипотеза принята, то это не означает,
что она подтверждена с заданной
вероятностью. Это лишь означает, что
гипотеза согласуется с опытными данными,
но возможно, что для другого эксперимента
гипотеза будет отвергнута.
Приведенные
рассуждения представляют собой простейший
вид статистической процедуры, называемой
проверкой гипотез. Предполагаем, что
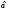 – несмещенная оценка параметра
– несмещенная оценка параметра – имеет плотность распределения
– имеет плотность распределения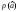 .
Если гипотеза
.
Если гипотеза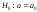 верна, то функция
верна, то функция
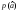 должна иметь среднее значение
должна иметь среднее значение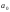 ,
как это показано на рис. 8.9.
,
как это показано на рис. 8.9.
Вероятность
того, что величина
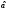 не будет превышать нижнего уровня
не будет превышать нижнего уровня ,
равна
,
равна
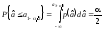 ,
,
а
вероятность того, что
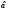 превзойдет верхнюю границу
превзойдет верхнюю границу ,
составит
,
составит
 .
.
Таким
образом, вероятность того, что
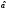 выйдет за пределы интервала с границами
выйдет за пределы интервала с границами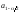 и
и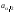 ,
составит
,
составит .
Величина
.
Величина выбирается настолько малой, чтобы
попадание
выбирается настолько малой, чтобы
попадание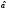 за пределы интервала, заключенного
между
за пределы интервала, заключенного
между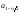 и
и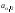 ,
было бы практически невозможным событием.
Если в результате эксперимента величина
,
было бы практически невозможным событием.
Если в результате эксперимента величина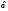 выходит за пределы интервала
выходит за пределы интервала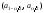 ,
то в этом случае есть серьезные основания
сомневаться в справедливости проверяемой
гипотезы
,
то в этом случае есть серьезные основания
сомневаться в справедливости проверяемой
гипотезы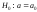 .
В самом деле, если гипотеза
.
В самом деле, если гипотеза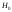 верна, то значение
верна, то значение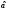 будет маловероятным, и поэтому гипотезу
о равенстве параметра
будет маловероятным, и поэтому гипотезу
о равенстве параметра величине
величине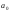 следует отвергнуть. С другой стороны,
если оценка
следует отвергнуть. С другой стороны,
если оценка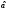 попадает
в интервал
попадает
в интервал ,
то нет серьезных оснований подвергать
сомнению справедливость проверяемой
гипотезы
,
то нет серьезных оснований подвергать
сомнению справедливость проверяемой
гипотезы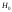 ,
и гипотезу о равенстве
,
и гипотезу о равенстве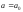 следует принять.
следует принять.
Малое
значение вероятности
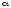 ,
используемое при проверке гипотезы,
называетсяуровнем
значимостикритерия. Интервал
значений
,
используемое при проверке гипотезы,
называетсяуровнем
значимостикритерия. Интервал
значений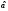 ,
для которых гипотезу следует отвергнуть,
называется областью отклонения гипотезы,
иликритической областью. Интервал
значений
,
для которых гипотезу следует отвергнуть,
называется областью отклонения гипотезы,
иликритической областью. Интервал
значений ,
при которых гипотезу следует принять,
носит названиеобласти принятия
гипотезы(см. рис. 8.9). Приведенный
способ проверки гипотезы называется
двусторонним критерием, так как если
гипотеза
,
при которых гипотезу следует принять,
носит названиеобласти принятия
гипотезы(см. рис. 8.9). Приведенный
способ проверки гипотезы называется
двусторонним критерием, так как если
гипотеза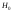 верна, то величина
верна, то величина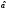 может быть как больше, так и меньше
может быть как больше, так и меньше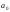 .
Необходимо проверять значимость
расхождения между
.
Необходимо проверять значимость
расхождения между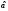 и
и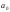 с обеих сторон. В некоторых задачах
может оказаться достаточно одностороннего
критерия. Например, пусть гипотеза
состоит том, что
с обеих сторон. В некоторых задачах
может оказаться достаточно одностороннего
критерия. Например, пусть гипотеза
состоит том, что
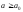 .
В этом случае гипотеза будет ошибочной
только тогда, когда
.
В этом случае гипотеза будет ошибочной
только тогда, когда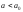 ,
а критерий будет использовать только
нижнюю границу плотности распределения
,
а критерий будет использовать только
нижнюю границу плотности распределения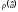 .
.
При
проверке статистических гипотез возможны
ошибки двух типов. Во-первых, гипотеза
может быть отклонена, хотя в действительности
она верна. Эта возможная ошибка называется
ошибкой первого
рода. Во-вторых, гипотеза принимается,
хотя фактически она неверна. Такая
ошибка называетсяошибкой
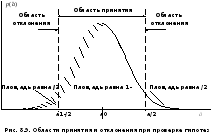
второго рода.Как видно на рис. 8.9, ошибка первого рода
происходит в том случае, когда при
справедливости гипотезы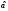 попадает в область ее отклонения. Таким
образом, вероятность ошибки первого
рода равна
попадает в область ее отклонения. Таким
образом, вероятность ошибки первого
рода равна ,
т. е. уровню значимости критерия.
,
т. е. уровню значимости критерия.

Для
того чтобы найти вероятность ошибки
второго рода, следует определить каким-то
образом величину отклонения истинного
значения параметра
 от гипотетического значения параметра
от гипотетического значения параметра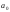 ,
которое требуется определить.
Предполагается, что истинное значение
параметра
,
которое требуется определить.
Предполагается, что истинное значение
параметра в действительности равно
в действительности равно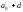 или
или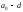 (см. рис. 8.10). Если согласно гипотезе
(см. рис. 8.10). Если согласно гипотезе ,
а на самом деле
,
а на самом деле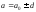 ,
товероятность
того, что
,
товероятность
того, что
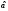 попадет в область принятия гипотезы
попадет в область принятия гипотезы ,
т.е. в интервал
,
т.е. в интервал ,
составляет
,
составляет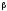 .
Таким образом, вероятность ошибки
второго рода равна
.
Таким образом, вероятность ошибки
второго рода равна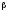 при выявлении отклонения истинного
значения параметра
при выявлении отклонения истинного
значения параметра на
на от гипотетической величины
от гипотетической величины .
.
Вероятность
 называетсямощностью
критерия. Понятно, что при заданном
значении
называетсямощностью
критерия. Понятно, что при заданном
значении (объеме опытных данных) вероятность
ошибки первого рода может быть сделана
сколь угодно малой за счет уменьшения
уровня значимости
(объеме опытных данных) вероятность
ошибки первого рода может быть сделана
сколь угодно малой за счет уменьшения
уровня значимости .
Однако при этом растет вероятность
.
Однако при этом растет вероятность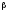 – ошибка второго рода (уменьшается
мощность критерия). Единственный способ
уменьшить и
– ошибка второго рода (уменьшается
мощность критерия). Единственный способ
уменьшить и ,
и
,
и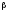 состоит в увеличении объема выборки
состоит в увеличении объема выборки ,
используемой при вычислении
,
используемой при вычислении .
Исходя из этих соображений определяется
объем необходимых опытных данных в
статистических экспериментах.
.
Исходя из этих соображений определяется
объем необходимых опытных данных в
статистических экспериментах.
Проверка гипотезы о равенстве статистических средних значений
При проведении статистических экспериментов со случайными величинами самой различной природы большое внимание уделяется воспроизводимости результатов опытов при неоднократном повторении серии экспериментов. Часто возникает ситуация, когда среднее значение в одной серии опытов заметно отличается от величины этого параметра в другой серии. Естественно возникает вопрос, чем объяснить обнаруженное расхождение средних значений: либо случайными ошибками, либо это расхождение вызвано какими-то незамеченными или даже неизвестными ранее закономерностями.
Пусть
над случайной величиной
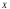 проводятся две серии опытов. Первая
серия объемом
проводятся две серии опытов. Первая
серия объемом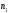 испытаний:
испытаний: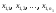 .
Вторая серия экспериментов объемом
.
Вторая серия экспериментов объемом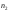 испытаний:
испытаний: .
При этом известно, что случайная величина
.
При этом известно, что случайная величина распределена по нормальному закону с
математическим ожиданием
распределена по нормальному закону с
математическим ожиданием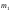 и дисперсией
и дисперсией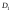 в первой серии опытов и параметрами
в первой серии опытов и параметрами и
и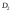 – во второй.
– во второй.
По
экспериментальным данным получены
статистические средние значения
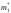 и
и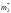 .
Необходимо проверить гипотезу
.
Необходимо проверить гипотезу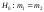 при альтернативной гипотезе
при альтернативной гипотезе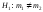 .
.
Для
случая, когда дисперсии
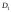 и
и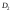 известны, оценки
известны, оценки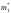 и
и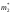 имеют нормальное распределение с
параметрами
имеют нормальное распределение с
параметрами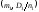 и
и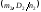 соответственно (см. 7.3 и 7.4). Так как
случайные величины
соответственно (см. 7.3 и 7.4). Так как
случайные величины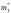 и
и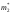 независимы, то их разность тоже имеет
нормальный закон распределения с
параметрами
независимы, то их разность тоже имеет
нормальный закон распределения с
параметрами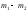 и
и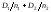 (нормальный закон устойчив к композиции).
(нормальный закон устойчив к композиции).
Таким образом, случайная величина
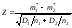 ,
,
которая является нормированной разностью оценок математических ожиданий, имеет нормальное распределение с нулевым математическим ожиданием и единичной дисперсией. Эта величина выбирается в качестве проверочной статистики.
Критическим для проверяемой гипотезы являются значения
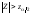 ,
,
где
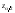 – квантиль порядка
– квантиль порядка стандартного нормального распределения,
т. е. значение гауссовой случайной
величины, вероятность попасть правее
которой равна
стандартного нормального распределения,
т. е. значение гауссовой случайной
величины, вероятность попасть правее
которой равна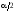 (см. рис. 8.9).
(см. рис. 8.9).
Когда
дисперсии
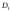 и
и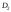 неизвестны, то сначала их необходимо
оценить по экспериментальным данным.
Пусть получены оценки
неизвестны, то сначала их необходимо
оценить по экспериментальным данным.
Пусть получены оценки и
и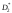 ,
которые незначительно отличаются друг
от друга. В этом случае считается, что
,
которые незначительно отличаются друг
от друга. В этом случае считается, что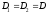 ,
и получают оценку так называемой
"объединенной" дисперсии, используя
результаты обеих серий опытов:
,
и получают оценку так называемой
"объединенной" дисперсии, используя
результаты обеих серий опытов:
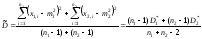 .
.
Случайная
величина
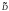 имеет распределение
имеет распределение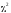 с
с степенями свободы. В качестве статистики
для проверки гипотезы о равенстве
математических ожиданий выбирается
случайная величина
степенями свободы. В качестве статистики
для проверки гипотезы о равенстве
математических ожиданий выбирается
случайная величина
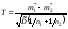 ,
,
имеющая
распределение Стьюдента с
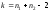 .
.
Критическими для проверяемой гипотезы являются значения
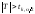 ,
,
где
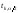 –
–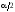 -процентная
точка распределения Стьюдента с
-процентная
точка распределения Стьюдента с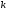 степенями свободы.
степенями свободы.
Пример.
В двух сериях опытов над нормальной
случайной величиной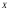 объемом соответственно
объемом соответственно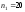 и
и испытаний оценены математические
ожидания и получено, что в первой серии
испытаний оценены математические
ожидания и получено, что в первой серии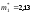 ,
а во второй –
,
а во второй –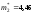 .
Дисперсия случайной величиныизвестна:
.
Дисперсия случайной величиныизвестна:
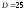 .
Нужно при уровне значимости
.
Нужно при уровне значимости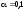 проверить нулевую гипотезу
проверить нулевую гипотезу при альтернативной гипотезе
при альтернативной гипотезе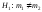 .
.
Значение
проверочной статистики
 равно
равно
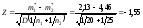 .
.
С
использованием табл. 8.4 получаем, что
 .
Так как
.
Так как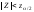 ,
то нулевая гипотеза принимается, т. е.
математические ожидания совпадают с
уровнем значимости 0,1.
,
то нулевая гипотеза принимается, т. е.
математические ожидания совпадают с
уровнем значимости 0,1.
Если
предположить, что дисперсия случайной
величины
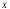 неизвестна, то ее оценки по результатам
обеих серий испытаний оказались равными:
неизвестна, то ее оценки по результатам
обеих серий испытаний оказались равными: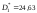 и
и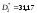 .
Кроме этого, предполагаем, что полученные
оценки мало отличаются одна от другой,
и поэтому вычисляем оценку объединенной
дисперсии по формуле
.
Кроме этого, предполагаем, что полученные
оценки мало отличаются одна от другой,
и поэтому вычисляем оценку объединенной
дисперсии по формуле
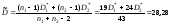 ,
,
а значение проверочной статистики
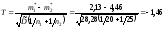 .
.
Используя таблицу процентных точек t-распределения Стьюдента (прил. 4), получаем
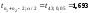 .
.
Так
как и в этом случае
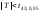 ,
то гипотеза о равенстве математических
ожиданий принимается.
,
то гипотеза о равенстве математических
ожиданий принимается.
Проверка гипотезы о равенстве двух дисперсий
Проверка
гипотезы о равенстве дисперсий особенно
важна в различных экспериментах над
случайными величинами, поскольку знание
дисперсии позволяет оценить степень
рассеивания случайной величины и
соответственно судить о точности и
надежности результатов. Как и в предыдущей
задаче, проводятся две серии опытов по
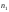 и
и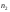 испытаний, а полученные экспериментальные
данные имеют нормальное распределение
с параметрами
испытаний, а полученные экспериментальные
данные имеют нормальное распределение
с параметрами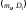 и
и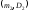 соответственно. По опытным данным
найдены несмещенные оценки
соответственно. По опытным данным
найдены несмещенные оценки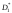 и
и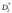 .
Ставится задача определить, лежит ли
различие между этими оценками в границах
возможных случайных изменений, т. е.
можно ли оба значения рассматривать
как оценки дисперсии одной и той же
случайной величины
.
Ставится задача определить, лежит ли
различие между этими оценками в границах
возможных случайных изменений, т. е.
можно ли оба значения рассматривать
как оценки дисперсии одной и той же
случайной величины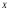 ,
имеющей нормальное распределение.
,
имеющей нормальное распределение.
Таким
образом, необходимо проверить гипотезу
 .
В качестве альтернативной гипотезы
выбирается гипотеза
.
В качестве альтернативной гипотезы
выбирается гипотеза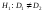 .
.
При сравнении дисперсий в качестве проверочной статистики выбирается случайная величина
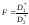 .
(8.26)
.
(8.26)
Распределение
величины
 находим из условия, что при справедливости
гипотезы
находим из условия, что при справедливости
гипотезы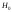 дисперсии равны, т. е.
дисперсии равны, т. е.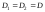 .
Поэтому перепишем выражение (8.26), учитывая
(8.19) в виде
.
Поэтому перепишем выражение (8.26), учитывая
(8.19) в виде
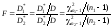 . (8.27)
. (8.27)
Соотношение
(8.27) не зависит от неизвестного параметра
 .
Случайная величина
.
Случайная величина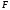 имеет распределение Фишера илиF-распределение
с
имеет распределение Фишера илиF-распределение
с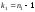 и
и степенями свободы.
степенями свободы.
Критическими для проверяемой гипотезы являются значения:
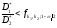 ;
;
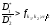 .
.
Для
сокращения объема таблиц процентных
точек распределенияФишера за
значение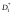 принимается большая из полученных
оценок дисперсии.
принимается большая из полученных
оценок дисперсии.
Пример.
В двух сериях опытов над нормальной
случайной величиной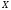 объемом
соответственно
объемом
соответственно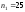 и
и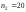 испытаний получены оценки дисперсии:
испытаний получены оценки дисперсии: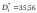 ;
;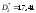 .
Необходимо проверить гипотезу о равенстве
гипотез при уровне
значимости
.
Необходимо проверить гипотезу о равенстве
гипотез при уровне
значимости
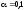 .
.
Величина проверочной статистики равна
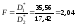 .
.
По таблице процентных точек F-распределения Фишера находим критическое значение
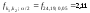 .
.
Получили,
что
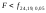 .
Поэтому нулевая гипотеза о равенстве
дисперсий принимается с уровнем
значимости 0,1.
.
Поэтому нулевая гипотеза о равенстве
дисперсий принимается с уровнем
значимости 0,1.
Критерий согласия
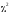
На
практике часто возникает задача
аппроксимации построенной гистограммы
аналитическим выражением, представляющим
собой некоторый теоретический закон
распределения (плотности вероятности
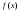 ).
При этом стремятся к тому, чтобы такая
аппроксимация была в определенном
смысле наилучшей. Заметим, что любая
аналитическая функция
).
При этом стремятся к тому, чтобы такая
аппроксимация была в определенном
смысле наилучшей. Заметим, что любая
аналитическая функция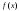 ,
с помощью которой аппроксимируется
статистическое распределение, должна
обладать основными свойствами плотности
распределения:
,
с помощью которой аппроксимируется
статистическое распределение, должна
обладать основными свойствами плотности
распределения:
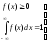 .
.
Чтобы
оценить, насколько хорошо выбранный
теоретический закон распределения
согласуется с экспериментальными
данными, используются так называемые
критерии согласия. Таких критериев
существует несколько, но наиболее часто
применяется критерий
согласия
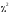 ,
предложенный Пирсоном.
,
предложенный Пирсоном.
Критерий
согласия
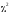 является непараметрическим критерием
проверки статистических гипотез в
отличие от ранее рассмотренных критериев,
которые являются параметрическими.
является непараметрическим критерием
проверки статистических гипотез в
отличие от ранее рассмотренных критериев,
которые являются параметрическими.
Пусть
проведено
 независимых опытов, в каждом из которых
случайная величина
независимых опытов, в каждом из которых
случайная величина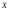 приняла определенное значение. Результаты
опытов сведены в
приняла определенное значение. Результаты
опытов сведены в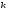 интервалов, и построены статистический
ряд, выборочная функция распределения
и гистограмма, т. е. экспериментальные
данные описываются выборочным законом
распределения
интервалов, и построены статистический
ряд, выборочная функция распределения
и гистограмма, т. е. экспериментальные
данные описываются выборочным законом
распределения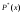 .
Необходимо проверить, согласуются ли
экспериментальные данные с гипотезой
.
Необходимо проверить, согласуются ли
экспериментальные данные с гипотезой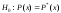 о том, что случайная величина
о том, что случайная величина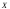 имеет выбранный теоретический закон
распределения
имеет выбранный теоретический закон
распределения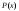 ,
который может быть задан функцией
распределения
,
который может быть задан функцией
распределения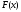 или плотностью
или плотностью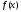 .
Альтернативная гипотеза в этом случае
–
.
Альтернативная гипотеза в этом случае
–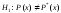 .
.
Знание
теоретического закона распределения
позволяет найти теоретические вероятности
попадания случайной величины в каждый
интервал (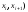 ,
,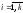 :
: .
.
Проверка
согласованности теоретического и
статистического распределений сводится
к оценке расхождений между теоретическими
вероятностями
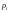 и полученными частотами
и полученными частотами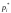 .
В качестве меры расхождения удобно
выбрать сумму квадратов отклонений
.
В качестве меры расхождения удобно
выбрать сумму квадратов отклонений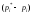 ,
взятых с некоторыми "весами"
,
взятых с некоторыми "весами"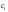 :
:
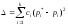 .
.
Смысл
коэффициентов
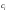 ("весов" интервалов) состоит в том,
что отклонения, относящиеся к разным
интервалам, нельзя считать одинаковыми
по значимости. То есть одно и то же по
абсолютной величине отклонение
("весов" интервалов) состоит в том,
что отклонения, относящиеся к разным
интервалам, нельзя считать одинаковыми
по значимости. То есть одно и то же по
абсолютной величине отклонение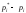 может быть мало значимым, если сама
вероятность
может быть мало значимым, если сама
вероятность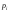 велика, и, наоборот, быть заметным, если
эта вероятность мала. Естественно, веса
велика, и, наоборот, быть заметным, если
эта вероятность мала. Естественно, веса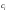 выбирать по величине обратно пропорционально
вероятностям
выбирать по величине обратно пропорционально
вероятностям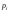 .
.
Пирсон
доказал, что если выбрать
 ,
то при больших
,
то при больших закон распределения случайной величины
закон распределения случайной величины (см. выражение 8.1) практически не зависит
от функции распределения
(см. выражение 8.1) практически не зависит
от функции распределения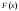 и числа испытаний
и числа испытаний ,
а зависит только от числа разрядов
,
а зависит только от числа разрядов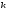 и стремится к распределению
и стремится к распределению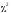 .
.
Обозначив
через
 меру расхождения
меру расхождения ,
получаем
,
получаем
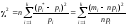 . (8.28)
. (8.28)
Распределение
 зависит от параметра
зависит от параметра ,
называемого числом "степеней свободы".
Для критерия согласия Пирсона
,
называемого числом "степеней свободы".
Для критерия согласия Пирсона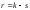 ,
где
,
где – число интервалов,
– число интервалов, – число независимых условий ("связей"),
накладываемых на частоты
– число независимых условий ("связей"),
накладываемых на частоты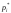 и параметры распределения. Так, при
аппроксимации нормального распределения
и параметры распределения. Так, при
аппроксимации нормального распределения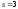 ,
а при исследовании распределения
Пуассона
,
а при исследовании распределения
Пуассона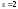 .
.
Схема
применения критерия
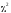 для оценки согласованности теоретического
и статистического распределения сводится
к следующим процедурам (этапам):
для оценки согласованности теоретического
и статистического распределения сводится
к следующим процедурам (этапам):
1.
На основании полученных экспериментальных
данных
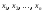 рассчитываются значения частот
рассчитываются значения частот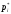 в каждом из
в каждом из интервалов.
интервалов.
2.
Вычисляются, исходя из теоретического
распределения, вероятности
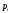 попадания значений случайной величины
в интервалы
попадания значений случайной величины
в интервалы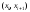 .
.
3.
По формуле (8.28) рассчитывается значение
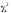 .
.
4.
Определяется число степеней свободы
 .
.
5.
По таблице процентных значений
распределения
 (прил. 3) определяется вероятность
(прил. 3) определяется вероятность того, что случайная величина, имеющая
распределение
того, что случайная величина, имеющая
распределение с
с степенями свободы превзойдет полученное
на этапе 3 значение
степенями свободы превзойдет полученное
на этапе 3 значение .
Если эта вероятность мала, то гипотеза
.
Если эта вероятность мала, то гипотеза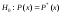 отбрасывается как неправдоподобная.
Если же эта вероятность относительно
велика, то гипотезу
отбрасывается как неправдоподобная.
Если же эта вероятность относительно
велика, то гипотезу можно признать не противоречащей опытным
данным.
можно признать не противоречащей опытным
данным.
Пример.
Пусть случайная величина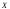 – значения напряжения на выходе
генератора шума. Проверим, согласуются
ли полученные данные с нормальным
законом распределения.
– значения напряжения на выходе
генератора шума. Проверим, согласуются
ли полученные данные с нормальным
законом распределения.
Получено
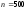 значений, при этом оценки математического
ожидания и среднего квадратичного
значения соответственно равны:
значений, при этом оценки математического
ожидания и среднего квадратичного
значения соответственно равны: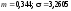 .
Для теоретического нормального
распределения с полученными параметрами
.
Для теоретического нормального
распределения с полученными параметрами и
и вычисляем вероятности попадания в
каждый из 10 интервалов по формуле
вычисляем вероятности попадания в
каждый из 10 интервалов по формуле
 ,
,
где
 – границы
– границы -го
интервала,
-го
интервала,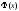 – функция Лапласа, таблица значений
которой приведена в прил. 2.
– функция Лапласа, таблица значений
которой приведена в прил. 2.
Затем
создается таблица, содержащая число
попаданий
 в
каждый разряд и соответствующие значения
в
каждый разряд и соответствующие значения для
для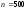 .
.
|
Интервалы |
-10-8 |
-8-6 |
-6-4 |
-4-2 |
-20 |
02 |
24 |
46 |
68 |
810 |
|
|
5 |
9 |
47 |
85 |
112 |
122 |
69 |
34 |
12 |
5 |
|
|
2,25 |
10,32 |
32,75 |
72,36 |
110,94 |
118,12 |
88,34 |
44,84 |
15,98 |
3,95 |
По формуле (8.28) получаем
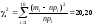 .
.
Так
как число степеней свободы
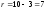 ,
то по таблице процентных точек
,
то по таблице процентных точек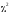 распределения (прил. 3) находим, что
распределения (прил. 3) находим, что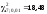 .
Поскольку
.
Поскольку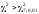 для малой вероятность
для малой вероятность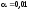 ,
следует признать:полученные
экспериментальные данные противоречат
проверяемой гипотезе о том, что случайная
величина
,
следует признать:полученные
экспериментальные данные противоречат
проверяемой гипотезе о том, что случайная
величина
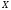 распределена по нормальному закону.
распределена по нормальному закону.
При
использовании критерия согласия (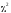 или любого другого) положительный ответ
нельзя рассматривать как утвердительный
о правильности выбранной гипотезы.
Определенным является лишь отрицательный
ответ, т. е. если полученная вероятность
или любого другого) положительный ответ
нельзя рассматривать как утвердительный
о правильности выбранной гипотезы.
Определенным является лишь отрицательный
ответ, т. е. если полученная вероятность мала, то можно отвергнуть выбранную
гипотезу
мала, то можно отвергнуть выбранную
гипотезу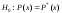 и отбросить ее как явно не согласующуюся
с экспериментальными данными. Если же
вероятность
и отбросить ее как явно не согласующуюся
с экспериментальными данными. Если же
вероятность велика, то это не может считаться
доказательством справедливости гипотезы
велика, то это не может считаться
доказательством справедливости гипотезы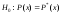 ,
а указывает только на то, что гипотеза
не противоречит экспериментальным
данным.
,
а указывает только на то, что гипотеза
не противоречит экспериментальным
данным.
При
использовании критерия согласия
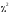 достаточно большими должны быть не
только общее число опытов
достаточно большими должны быть не
только общее число опытов (несколько сотен), но и значения
(несколько сотен), но и значения в отдельных интервалах. Для всех
интервалов должно выполняться условие
в отдельных интервалах. Для всех
интервалов должно выполняться условие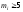 .
Если для некоторых интервалов это
условие нарушается, то соседние интервалы
объединяются в один.
.
Если для некоторых интервалов это
условие нарушается, то соседние интервалы
объединяются в один.