14* Признаки сравнения

Первый признак сравнения

Пусть даны 2 положительных ряда и .

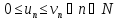
а) если сходится, то исходится.

б) если расходится, то ирасходится

Доказательство:

Ряд v сходится.

Второй признак сравнения

Если для двух положительных рядов 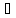конечный и 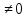предел, то оба ряда ведут себя одинаково.

15* Признаки Даламбера и Коши

Признак Даламбера

Пусть для знакоположительного ряда предел отношения последующего члена к предыдущему =e, тогда:

а) если е<1 – ряд сходится

б) если е>1 – ряд расходится

в) если е=1 – то признак ответа не дает

Признак Коши

Пусть для знакоположительного ряда =e, тогда:

а) если е<1 – ряд сходится

б) если е>1 – ряд расходится

в) если е=1 – то признак ответа не дает

16* Интегральный признак Коши. Ряд Дирихле

Пусть члены знакоположительного ряда 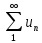представляют целочисленные значения непрерывной, положительной и монотонно убывающей функции, тогда: если

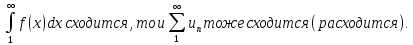
17* Знакопеременные ряды. Признак Лейбница

Ряд знакопеременный, если в нем есть и положительные и отрицательные члены. Если любые 2 члена разных знаков, то ряд знакочередующийся.

Признак Лейбница

Если члены знакочеред. ряда монотонно убывают, то ряд сходится, его сумма положит. и не превосходит первого члена.

Следствие 1. Остаток ряда Лейбницского типа сходится и модуль его суммы не превосходит модуля первого члена остатка.

Следствие 1. Абсолютная погрешность, полученная от замены суммы ряда Лейбницского типа и его частичной суммы не превосходит по модулю первого члена остатка.

17. Знакопеременные ряды. Признак Лейбница.

Знакочередующийся ряд-ряд вида:

Признак Лейбница(достаточный признак сходимости знакочередующихся рядов):

Пусть для знакочередующегося ряда () члены ряда монотонно убывают по абсолютной величене, тогда данный ряд сходится и его сумма положительна и не превосходит первого члена.

Доказательство:

Рассмотрим сумму чётного числа членов:

Существует

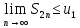
Тоже самое для нечётных =>

Ряд удовлетворяющий признаку Лейбница наз рядом Лейбницкого типа.

Следствие:

Абсолютная погрешность, получаемая от замены сумма ряда Лейбницкого типа его частичной суммой не превосходит по модулю первого члена остатка.

Теорема:

Если ряд из модулей сходится, то и сам ряд сходится.

18. Абсолютно и условно сходящиеся ряды.

Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из его модулей.

Знакопеременный ряд называется условно сходящимся,если сам ряд сходится, а ряд из его модулей расходится.

Для выяснения абсолютной сходимости выясняют сходимость ряда из модулей, для этого используют все признаки сходимостизнакоположительных рядов. Если ряд из модулей расходится, то данный ряд может сходиться и расходиться. Исключениями будут являться признаки Даламбера и Коши, т.к. в них не выполняется необходимый признак сходимости ряда(стремится к 0=> ряд расходится)