Методичка по математике.1 курс.1 семестр.ФЭИС

Составим характеристическое уравнение:

	8 − λ	5	3		= (8 − λ) ((2 − λ) (1− λ)− 6)= (8 − λ) (λ2 −3λ − 4)= 0.
	0	2 − λ −6
	0	−1	1− λ

Решая полученное уравнение, получим λ1 = 8 , λ2 = −1, λ3 = 4 – собст-

венные значения матрицы А.

Для каждого из полученных собственных значений найдем собственные векторы матрицы А.

	8 −8		5	3		0 5			3
1) Если λ = 8 , то		0	2 −8	−6			0	−6	−6
	A − λE =					=
		0	−1	1−8			0	−1	−7

и матричное уравнение выглядит:
0		5	3	x			0
	0 −6		−6	1			0
				x2		=		.
	0	−1	−7				0
				x3

Этому уравнению соответствует однородная система линейных урав-

5x2 + 3x3 = 0;

нений −6x2 − 6x3 = 0;

−x2 −7x3 = 0.

Из второго уравнения x2 = −x3 , тогда оставшиеся два уравнения будут иметь вид:

−5x

3

+ 3x

3

= 0;

−2x

3

= 0;

x

= 0, x

= 0, x

= m, m , m ≠ 0.

3

2

x3 −7x3 = 0;

−6x3 = 0;

1

m

Вектор X1 = 0 , m , m ≠ 0 – собственный вектор матрицы А.

0

2) Если λ = −1, то получим однородную систему линейных уравнений:

9x1 + 5x2 + 3x3 = 0;

9x + 5x

+ 3x

= 0;

= −

13

x

;

3x2 − 6x3 = 0;

x

9

1

2

3

1

3

− x2 + 2x3 = 0;

− x2 + 2x3 = 0;

= 2x3;

x2

x3 = 9k, x2 =18k, x1 = −13k, k , k ≠ 0.

−13k

Тогда вектор X2 = 18k , k , k ≠ 0 – собственный вектор матрицы А.

9k

21

3) Если λ = 4, то получим однородную систему линейных уравнений:

4x + 5x

+ 3x

= 0;

4x

+ 5x

+ 3x

= 0;

x = 3x

;

1

2

3

= 0;

− 2x2 − 6x3

1

2

3

1

3

− x2

−3x3

= 0;

− x2 −3x3 = 0;

x2 = −3x3;

x3 = t, x2 = −3t, x1 = 3t, t , t ≠ 0.

3t

Тогда вектор X3

, t , t ≠ 0

– собственный вектор матрицы А.

= −3t

t

m

−13k

3t

Ответ.

X1

0

, X2

=

18k

, X3

−3t

≠ 0,k ≠ 0, t ≠ 0.

=

=

, m,k,t , m

0

9k

t

Задания для аудиторной работы

43. Для заданной матрицы А и векторов X1, X2, X3 установить, какие из

данных векторов являются собственными векторами матрицы А и найти их собственные значения, если:

а)		1	−2			2				0		=	1
	A =		,		X1 =		, X2			=	, X3			3	;
		−2 3				2				0
		0 0 1					3				−1				−1
б)		1 0 0			, X1		3								3
	A =					=			, X2 =		−1 , X3		=			.
		0 1 0					3								2
											−1
44. Найти собственные числа и собственные векторы матрицы А:
		1	−1							5 2 21						9 −8 0
а)										0 3 0							10 −9 0
	A =	2	;			б) A =						;				в) A =		.
			4							1 −2 1							−12 12 3

Задания для индивидуальной работы

45. Для заданной матрицы А и векторов X1, X2, X3 установить, какие из

данных векторов являются собственными векторами матрицы А и найти их собственные значения, если:

а)		5	−4					1	, X2			2		, X3			3		;
	A =	6	−5	, X1 =								=					=
								1				3					4
		3	2	1					1					2					1
б)		2	4	2		, X1			0		,	X2 =		2		,	X3 =		0
	A =						=													.
		1 2		3					2					0
																			−1

22

46. Найти собственные числа и собственные векторы матрицы А:

а)	A =	5 2												б)				3 −4									в)						13 5		;
				2 8			;									A =				7 1				;					A =
																																		5 13
г)	0 3													д)						2 3				;			е)							1 2
	A =					;										A =													A =					.
			3 8																	3 2													−2 5
47. Найти собственные числа и собственные векторы матрицы А:
		11 −6									2							1 2 −2															1 1 0
а)	A =			−6 10							−4		; б)											3			в)						0 1 0			;
																A = 1 0									;				A =
				2			−4 6																	0									5 3 2
																		1 3
	1 4 3																	5 6							3									3 1 0
г)			0 2				1							д)						−1 0							е)						−4 −1 0
	A =								;							A =									1 ;				A =								.
			0 0 3																		1 2													4 −8 −2
																								−1
Ответы. 46.							а) λ1 = 4,								=		−2				, λ2 = 9,						1						;
														x1				1							x2	=	; б)
																											2
в) λ1	= 8,				=		1			,	λ2 =18,							=	1			; г)							1								3
		x1														x2								λ1 = 9, x1 =					3		, λ2 = −1, x2					=	.
							−1												1																		−1
					6, x =					−2						= 3, x						1				18, x						2
47. а) λ			=								−1		,	λ						2	=		2	,λ =					=			−2		;
	1						1							2											3			3
											2												2									1
б) λ =1, x						−2					λ = 3, x							0					λ = −3, x						6
					=		1			,							=		1		,						=		−7		.
1				1							2					2							3			3
							1												1										5

АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ

7 Векторы в 2 и 3. Линейная зависимость и независимость

векторов. Скалярное произведение векторов

Вектором называют направленный отрезок или упорядоченную пару (тройку) чисел. Векторы, параллельные одной прямой или лежащие на прямой, называются коллинеарными. Векторы, лежащие в одной плоскости или параллельные одной и той же плоскости, называются компла-

нарными.

Проекцией вектора AB на ось Ox называется длина отрезка CD этой оси, заключенного между основаниями перпендикуляров, проведенных

из начальной и конечной точек вектора AB , взятая со знаком плюс, если

23

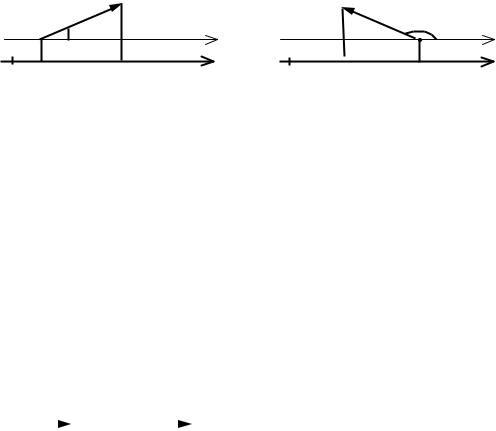
направление отрезка CD совпадает с направлением оси проекции (рис. 1), и со знаком минус, если эти направления противоположны (рис. 2).

		B			B
	A	α				α
						A
			x				x
	0 C	D		0	D	C
		Рисунок 1				Рисунок 2

Проекция вектора на ось равна длине вектора, умноженной на косинус угла между вектором и осью:

прOx AB =| AB | cosα.

Проекции вектора на координатные оси называются координатами

вектора: a = (x;y;z); AB = (xB − xA;yB − yA;zB − zA ).

Линейными операциями над векторами называют сложение и вычи-

тание векторов, умножение вектора на постоянное число.

Если векторы a и b заданы своими координатами a = (x1;y1;z1),

b = (x2;y2;z2 ), то a ± b = (x1 ± x2;y1 ± y2;z1 ± z2 ).

Если λ , λ = const , то a λ = λ a = (λx1;λy1;λz1), т.е. при умножении вектора на число все его координаты умножаются на это число.

А								В			Рассмотрим отрезок АВ, A ≠ B . Гово-
			С								рят, что точка С делит отрезок АВ в от-
			Рисунок 3								ношении λ , если AC = λCB (рис. 3).
											Число λ называют простым отноше-

нием трех точек и обозначают λ = (AB,C). Координаты точки С, делящей отрезок АВ в отношении λ, λ ≠ −1 находят по формулам:

x	c	=	λxb + xa ; y		c	=	λyb + ya ; z =		λzb + za	.
			1+ λ				1+ λ	c	1+ λ
Система векторов a1, a2,...,am							называется линейно зависимой, если

существуют такие постоянные c1, c2, ..., cm , одновременно неравные ну-

лю, что имеет место равенство c1a1 + c2 a2 +... + cmam = 0. В противном

случае система векторов называется линейно независимой.

На плоскости два любых коллинеарных вектора линейно зависимы, и наоборот, два любых неколлинеарных вектора линейно независимы.

В пространстве три любых компланарных вектора являются линейно зависимыми. Три вектора, не лежащие в одной плоскости, будут линейно независимыми.

Базисом в 2 ( 3 ) называют два неколлинеарных (три некомпланарных) вектора, взятых в определенном порядке. В качестве базиса будем рассматривать два (три) взаимно перпендикулярных вектора

24

единичной длины: i = (1; 0), j = (0; 1) (i = (1; 0; 0), j = (0; 1; 0), k = (0; 0; 1)).

Тогда a 2, a = (x; y) можно представить разложением по ортогональному базису в виде a = x i + y j . Аналогично, если a 3, a = (x; y; z),

то a = x i + y j + z k .

Косинусы углов, которые вектор a = (x; y; z) образует с координатными осями, называются направляющими косинусами этого вектора:

cosα =

x

, cos β =

y

, cosγ =

z

,

x2 + y2 + z2

x2 + y2 + z2

x2 + y2 + z2

cos2 α + cos2 β + cos2 γ =1.

Скалярным произведением двух векторов называется число, равное произведению длин этих векторов на косинус угла между ними:

a b =| a | | b | cosϕ; a b =| a | прab=| b | прba.

Отметим, что a b = 0 тогда и только тогда, когда векторы перпендикулярны или хотя бы один из них нуль-вектор.

Скалярное произведение векторов обладает свойствами коммутативности (a b = b a), ассоциативности относительно скалярного множите-

ля (λab = aλb = λab); дистрибутивности (a				(b	+ c )= ab					+ ac ). Скалярный
квадрат вектора равен квадрату его длины (a a =							a		2 ).
Если	векторы	a и b	заданы своими	координатами a = (x1;y1;z1),
b = (x2;y2;z2 ), то их скалярное произведение равно сумме произведений
одноименных координат: a			b = x1x2 + y1y2 + z1z2.

Механический смысл скалярного произведения. Если материаль-
ная точка, на которую действует сила F , совершает перемещение вдоль
вектора s , то работа А силы равна скалярному произведению вектора
силы на вектор перемещения: A = F				s.
	Задания для аудиторной работы
48. Задан правильный шестиугольник ABCDEF,
					AB = p ,		AE	= q . Найти
		,
вектора AC	, AD , AF		EF .
		=	(5; 10; 15) и		построен треугольник
49. На векторах OA				OB = (0; 10; 5)

ОАВ. Точка М делит сторону АВ в отношении 2:3. Найти координаты и

длину вектора OM .

25

50.

Даны векторы a = (3; − 2; 6)

и b = (−2; 1; 0). Найти координаты векто-

1

1

ров 2a −

3

b ;

2

a + b ; 2a + 3b .

51.

При каких α и β векторы a = (−2;3;β) и b = (α;−6;2)

коллинеарны?

52.

Дана прямоугольная трапеция ABCD, длины оснований AD и BC ко-

торой соответственно равны 4 и 2, а D = 45 . Найти проекции векторов

AD , AB , BC , AC

на ось, определяемую вектором CD .

x2 = (−1; 3; 2; 1) ,

53.

Показать,

что

векторы

x1 = (1; 2; 1; 2) ,

x3 = (−13; −1; 2; −11) линейно зависимы. Найти эту зависимость.

54.

Даны

четыре

вектора

a

= (4; 5; 2), b = (3; 0; 1), c = (−1; 4; 2)

и

d = (5; 7; 8) в некотором базисе. Показать, что векторы a, b и c

образу-

ют базис, и разложить вектор d

по этому базису.

55.

Даны векторы

a

= e1 + e2 + e3, b

= 2e1 −e2, c = 3e3 в базисе

e1, e2, e3 .

Показать, что векторы a, b и c

также образуют базис. Найти координаты

вектора d

= 6e1 −3e2

+ e3

в базисе a, b

, c .

b

56.

Векторы a

и b образуют угол ϕ =

2π

. Зная, что

a

= 3 и

= 4, вы-

3

числить a b ,

a2 (a − b)2 ,

(3a − 2b)(a + 2b).

57.

Даны векторы

a = (4; − 2; − 4)

и

b = (6; −3; 2).

Вычислить:

а)

a b ;

б)

a2

; в) (2a −3b)(b + 3a); г) (a − b)2 .

58.

Проверить,

могут ли векторы a = 7i + 6 j − 6k ,

b = 6i

+ 2 j + 9k быть

ребрами куба. Найти третье ребро куба.

59.

Пусть в треугольнике AOB : OA = a , OB = b ,

a

= 2,

b

= 4 , угол между

π

и стороной OA .

векторами a и b ϕ =

3 . Найти угол между медианой OM

60.

Определить работу силы F ,

F

=15 Н, которая действует на тело,

вызывая его перемещение на 4 м под углом π3 к направлению действия силы.

Задания для индивидуальной работы

61. Найти линейную комбинацию 3a1 + 5a2 −a3	векторов a1 = (4; 1; 3; − 2),
a2 = (1; 2; −3; 2) , a3 = (16; 9; 1; −3) .

26

62.Вектор a составляет с координатными осями Ох и Оу углы α = 60 и β =120 . Вычислить координаты вектора, если его длина равна 2.

63.Отрезок AB разделен точками M1,M2,M3,M4 на пять равных частей.

Найти координаты точек M1 и M3 , если A(−1;8;3), B (9;−7;− 2).

64.Найти координаты концов А и В отрезка, который точками C (2;0;2) и D(5;− 2;0) разделен на три равные части.

65.При каком α векторы m = (−1; 3) и n = (2;α) линейно зависимы?

66. Векторы		заданы в ортонормированном базисе i , j, k :		a = (1;1; 2),
e1 = (2;2;−1),		e2 = (0;4;8), e3 = (−1;−1;3). Показать, что векторы e1, e2, e3
образуют базис, найти разложение вектора a по этому базису.
67. Даны три вектора p, q, r . Найти разложение вектора a				по базису
p, q, r .
а)	p = (4; 5; 1), q = (3; 4; 1), r = (2; 3; 2), a = (6;3;4);
б)	p = (−1; 4; 3), q = (3; 2; − 4), r = (−2; −7; 1), a = (6;20;−3);
в)	p = (5; 7; − 2), q = (−3; 1; 3), r = (1; − 4; 6),		a = (14;9;−1);
г)	p = (1; −3; 1), q = (−2;−4; 3), r = (9; − 2; 3),		a = (−8;−10;13).

68.Пусть a = (1;−1;2), b = (2;− 2;1). Найти прb (3a − b).

69.Даны векторы a = (1;2;3), b = (−2;3;−1). Найти: а) координаты вектора

2a − 31 b ; б) угол между векторами a и b ; в) прb а.

70. Найти координаты вектора a , если известно, что он направлен в противоположную сторону к вектору b = 5i − 4 j + 22k , и его модуль равен 5.

71. Дано разложение вектора c по базису i , j, k : c =16i −15 j +12k .

Определить разложение по этому же базису вектора d , параллельного вектору c и противоположного с ним направления, при условии, что

| d |= 75 .

72.Даны точки А(–2; 3; –4), В(3; 2; 5), С(1; –1; 2), D(3; 2; –4). Вычислить проекцию вектора AB на направление вектора CD .

73.Даны три вектора a, b, c . Найти проекцию вектора 3a − 2b на на-

правление вектора c , если:

а) a = 5i − 6 j − 4k, b = 4i + 8 j −7k, c = 3 j − 4k ;

27

б) a = −9i + −4k, b = 2i − 4 j + 6k, c = 3i − 6 j + 9k ; в) a = 4i −5 j − 4k, b = 5i − j , c = 4k + 2 j −3k ;

г) a = 3i − j + 5k, b = 2i − 4 j + 6k, c = i − 2 j + 3k .

74.Даны вершины треугольника А, В и С. Определить внешний угол при вершине В, если:

а) А(–2; –5; –1), В(–6; –7; 9), С(4; –5; 1); б) А(5; 2; 7), В(7; –6; –9), С(–7; –6; 3); в) А(7; –1; –2), В(1; 7; 8), С(3; 7; 9); г) А(–7; –6; –5), В(5; 1; –3), С(8; –4; 0).

75.Векторы a и b взаимно перпендикулярны, а вектор c образует с

|= 5, | c |= 8 , вычислить:

а) (3a − 2b)(b

3

+ 3c ); б) (3a + 2b −3c )2 .

76.

При каких значениях α

векторы a + βb

и a − βb

перпендикулярны,

если

a

= 3 ,

b

= 5.

2

77.

найти:

2

,

2

,

Для векторов a = (4;− 2;

− 4), b = (6;−3;2)

a b , a

b

, (a + b)

(a − b)2 , (3a − 2b) (a + 2b).

78.

Найти 2a2

− 4ab + 5b2 , если a = (1;− 2;2), b = (2;− 2;−1).

79.

Найти работу равнодействующей сил F1 = i − j

+ k

и F2

= 2i + j

+ 3k

при перемещении ее точки приложения из начала координат в точку

М(2; –1; –1).

80. Даны три силы F1, F2 , F3 , приложенные к одной точке. Вычислить работу равнодействующей этих сил, совершаемую при перемещении

вдоль отрезка M1M2 , если:
а)									= (−3; − 2; 4) ,M1(5; 3; −7),M2(4; −1; − 4);
	F1		=	(3; − 4; 2) ,F2		= (2; 3; −5),F3
б)	F1 = (3; −1; −3), F2 = (3; 2; 1) ,							F3 = (−4; 1; 3) , M1(−1; 4; − 2), M2(2; 3; −1);
в)	F1 =			(3; − 2; 4)	, F2 = (−4; 4; −		3)	,	F3 = (3; 4; 2), M1(1; − 4; 3), M2(4; 0; − 2);
									= (−5; 4; 3), M1(−5; 0; 4) , M2(4; −3; 5);
г)	F1	= (7; 3;− 4),			F2	= (3; − 2; 2)	, F3
									= (7; 3; −1),M1(−3; − 2; 5),M2(9; −5; 4);
д) F1			=	(4; − 2; 3) ,F2		= (−2; 5; 6)	,F3
81. Известно, что | a |=13, | b |=19, | a + b |= 24. Вычислить | a − b |.
82. Найти значение параметра m, при котором векторы a = mi −3 j + 2k
и b = i				+ 2 j − mk взаимно перпендикулярны.

28

83.	Найти координаты вектора	b , коллинеарного вектору a = (2; 1; −1),
при условии, что их скалярное произведение равно 3.
84.	Найти вектор x , зная,	что он	перпендикулярен векторам
a = (2; 3; −1), b = (1; − 2; 3) и удовлетворяет условию x (2i				− j + k )= −6.
85.	Даны три вектора a = 2i − j + 3k, b = i		−3 j + 2k, c = 3i	+ 2 j − 4k . Най-

ти вектор x , удовлетворяющий условиям x a = −5, x b = −11, x c = 20 .

86.Найдите единичный вектор, перпендикулярный к оси Oy и вектору a = (4;3;2).

87.Найдите вектор x , коллинеарный вектору a = (1;2;−3) и удовлетво-

ряющий условию x a = 28 .

3p

+ q

q

− p

p

+ q

Ответы. 48.

AC

=

,

AD

= p

+ q ,

AF =

,EF = −

.

2

2

2

49. (3; 10;

11).

52.

пр

AD = 2

2

;

пр

AB = −

2;

пр BC =

2;

CD

CD

CD

пр AC = 0 . 53. 8x

−5x

2

+ x

3

= 0

. 54. (–1; 4; 3). 55. (0; 3; 1/3). 56. –6; 9;

CD

1

25 i +

20 j −

k .

37; –61. 58.

c = ±(6i

−9 j

− 2k ). 60. 30

Дж. 70.

a = −

10

2

1

2

7

7

7

79. 2 ед.раб. 86. e

= ±

; 0;

−

.

5

5

8 Векторное произведение векторов

Упорядоченная тройка некомпланарных векторов с общим началом называется правой, если при наблюдении из конца третьего вектора кратчайший поворот от первого вектора ко второму виден в направлении, противоположном направлению движения часовой стрелки. В противном случае тройка векторов называется левой.

Векторным произведением вектора a на вектор b называется вектор a ×b , длина которого численно равна площади параллелограмма, построенного на этих векторах | a ×b |=| a | | b | sinα , который перпендику-

лярен плоскости векторов a и b и направлен так, чтобы тройка векторов a, b, a ×b была правой.

Отметим, что a ×b = 0 тогда и только тогда, когда векторы коллинеарны или хотя бы один из них нуль-вектор.

Векторное произведение векторов обладает свойствами антикоммута-

тивности (a ×b = −b ×a); ассоциативности относительно скалярного множителя (λa ×b = a ×λb = λ(a ×b)); дистрибутивность: (a ×(b +c )= a ×b +a ×c ).

29

Если векторы a и b заданы своими координатами a = (x1;y1;z1),

b = (x2;y2;z2 ), то их векторное произведение равно
a ×b	=		i	j	k		.
			x1	y1	z1
			x2	y2	z2

Механический смысл векторного произведения. Пусть некоторое

твердое тело неподвижно закреплено в точке А, а в точке В этого тела
приложена сила F . В этом случае возникает вращающий момент, чис-
ленно равный произведению			| sinα.	В механике его принято
	| AB | | F
называть моментом силы: M = AB ×F .

Задания для аудиторной работы

b

88.

Векторы a

и b образуют угол

ϕ = 5π . Зная, что

a

= 2

и

= 6, вы-

числить a ×b ,

(2a + 3b)×(a − 4b)

.

6

89.

образуют угол ϕ =

π

и

|= 5 . Вы-

Известно, что векторы a и

b

4

| a

|=| b

числить площадь треугольника,

построенного на

векторах

a − 2b

и

3a

+ 2b .

б) (3a − b)×(a − 2b);

90. Пусть a = (3;−1;− 2), b = (1;2;−1). Найти: а) a ×b ;

в) (2a + b)×b .

91.

Найти площадь треугольника с вершинами А(1; 2; 0), В(3; 2; 1) и

С(–2; 1; 2).

a = (2; − 2; 1)

92.

Вычислить

синус угла, образованного векторами

и

b = (2; 3; 6) .

93.

Даны вершины треугольника А(1; –1; 2), В(5; –6; 2) и С(1; 3; –1). Вы-

числить длину его высоты BD.

, перпендикулярного оси аппликат и

94.

Найти координаты вектора

x

вектору a = (8; −15; 3) . Вектор

x

образует острый угол с осью абсцисс;

x

= 51.

95.

Твердое тело закреплено в точке А(2; 1; 3). В точке В(0; 1; 3) этого

тела приложена сила F = (0; 4; 3). Найти момент силы относительно точки А и направляющие косинусы момента.

30