Лекция № 42. Тема 5 : Линейные ду высших порядков
5.1. Линейные ду п-го порядка
Общий вид линейного дифференциального уравнения п-го порядка (ЛДУ - п)
.
(1)
Ему соответствует однородное уравнение п-го порядка
(2)
Определение 1.
Функции
называются линейно зависимыми (ЛЗ) на
,
если
,
где, по крайней мере, одно из них отличное
от нуля, для которых выполняется
.
В противном случае функции называются
линейно независимыми (ЛНЗ).
Для выяснения ЛЗ или ЛНЗ решений уравнения (2) также используется определитель Вронского, который для данного случая имеет вид
При этом, если
,
то система функций ЛЗ. Если же для
п
частных решений
уравнения (2)
,
то эти решения являются ЛНЗ.
Справедливы также теоремы о структуре решений уравнений (1-2):
Теорема 1.
Если
ЛНЗ решения уравнения (2), то его общее
решение имеет вид
,
где
произвольные константы.
Теорема 2.
Общее решение ЛНДУ - п
есть сумма частного решения
уравнения (1) и общего решения
соответствующего однородного (2), т.е.
.
Доказательства этих теорем аналогичны, как и для случая ЛДУ – 2.
Если известно
общее решение соответствующего
однородного уравнения (2), то общее
решение уравнения (1) можно находить
методом вариации произвольных постоянных.
Тогда система для нахождения функций
имеет вид
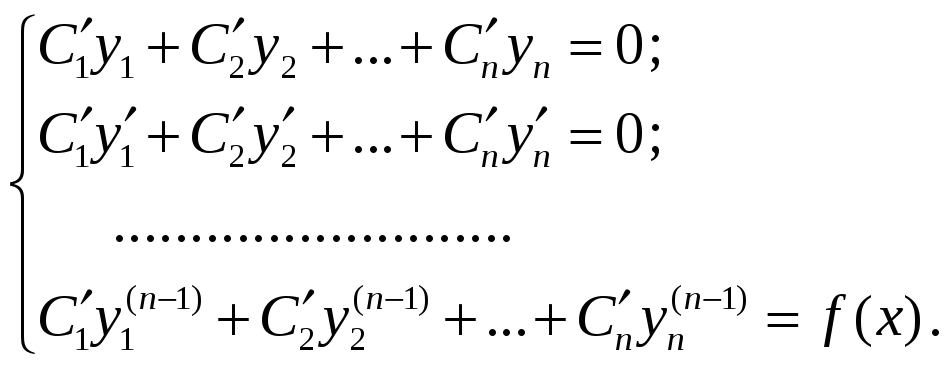
Остановимся на
случае, когда все коэффициенты
в уравнениях (1-2) являются константами.
Тогда для однородного уравнения имеем
характеристическое уравнение
.
(3)
По характеру корней уравнения (3) определяются частные ЛНЗ решения:
Правило. Каждому действительному корню k характеристического уравнения (3) т-ой кратности соответствует т ЛНЗ решений вида
.
Каждой паре
комплексных корней
кратности т
соответствует 2т
ЛНЗ решений вида
Для случая уравнения
со специальной правой частью
исполь-зуется аналогичное правило, как
и для ЛНДУ-2, для нахождения вида частного
решения
.
Пример 1. Найти общее решение ДУ
.
Ему соответствует однородное уравнение
Составим характеристическое уравнение
.
Найдём его корни
.
Тогда, согласно правилу, получаем общее решение однородного уравнения
.
Частное решение
неоднородного уравнения будем искать
в виде
,
где
частное решение уравнения
(4)
а
частное решение уравнения
(5)
Так как число 2
не является корнем характеристического
уравнения, то
.
Подставим это выражение в уравнение
(4), предварительно сократив его на
:
.
Частное решение уравнения (5) ищем в виде
,
так как нуль является корнем характеристического уравнения.
Подставим это выражение в уравнение (5):
.
Таким образом, получаем общее решение данного уравнения
.
5.2*. Понятие о краевой задаче
При решении некоторых задач требуется проинтегрировать ДУ не при начальных условиях (задача Коши), а с учётом значений искомой функции или её производных в некоторых точках. Условия, налагаемые на значения функции, её производных на концах отрезка, называются краевыми условиями, а соответствующая задача – краевой задачей.
При этом для корректности решаемой задачи число таких условий должно быть равно числу констант в общем решении. Такие задачи рассматриваются в курсе сопротивления материалов, а ещё более общие задачи встречаются в курсе уравнений математической физики.
Рассмотрим в качестве примера задачу изгиба балки на упругом основании.
y
q(x)
-l O l x
Дифференциальное уравнение прогиба балки имеет вид
,
где упругая постоянная, характеризующая свойства основания, Е - модуль упругости балки, I - момент инерции площади поперечного сечения балки, q(x) интенсивность внешней нагрузки.
Этому уравнению соответствует однородное уравнение
,
для которого характеристическое уравнение имеет вид
.
Непосредственно легко проверить, что его корнями являются
.
Этим корням соответствует общее решение
.
.
Рассмотрим случай,
когда
.
Тогда частное
решение будем искать в виде
.
Подставим это выражение в уравнение
прогиба балки, получим
.
Тогда
.
(6)
Константы
определяются из условий закрепления
концов балки, так, например, если концы
балки закреплены жестко, то эти условия
(граничные условия) имеют вид
.
Подставляя в эти
граничные условия полученное
выражение
для прогиба (6),
получим систему
четырёх
уравнений
для определения
.