
- •Аналитическая геометрия Лекция № 7. Тема 1 : Линии на плоскости и их уравнения
- •1.1. Линии и их уравнения в декартовой системе координат
- •1.2. Параметрические уравнения линий
- •1.3. Уравнение линии в полярной системе координат
- •1.4. Преобразование системы координат.
- •Лекция № 8. Тема 2 : Прямая линия на плоскости
- •2.1. Уравнения прямой линии
- •2.2. Угол между двумя прямыми
- •2.3. Взаимное расположение двух прямых
- •2.4. Уравнение прямой, проходящей через две точки
- •2.5. Уравнение прямой, проходящей через точку с заданным угловым коэффициентом
- •2.6. Расстояние от точки до прямой
- •Лекция № 9. Тема 3 : Линии второго порядка
- •3.1. Эллипс
- •3.2. Гипербола
- •10.3. Парабола
- •10.4. Классификация линий второго порядка
- •Лекция № 10. Тема 4 : Плоскость
- •4.1. Уравнение плоскости. Построение плоскости
- •4.2. Уравнение плоскости, проходящей через заданную точку, перпендикулярно заданному вектору
- •4.3. Уравнение плоскости, проходящей через три заданные точки
- •4.4. Угол между двумя плоскостями
- •4.5. Расстояние от точки до плоскости
- •Тема 5 : Прямая в пространстве
- •5.1. Уравнения прямой
- •Лекция № 11.
- •5.2. Уравнение прямой, проходящей через две точки
- •5.3. Угол между двумя прямыми
- •5.4. Расстояние от точки до прямой
- •5.5. Угол между прямой и плоскостью
- •5.6. Пересечение прямой с плоскостью
- •Лекция № 12. Тема 6 : Поверхности
- •6.1. Уравнение поверхности
- •6.2. Поверхности второго порядка
1.4. Преобразование системы координат.
Уравнение линии в новой системе координат

1.
Параллельный перенос ДСК. у
![]()
Рассмотрим две ДСК, имеющие М
одинаковое
направление осей, но
![]()
![]()
различные начала
координат.
![]()
![]()
В системе координат
Оху
точка
![]()
![]() относительно
системы
относительно
системы
![]() О
О
![]() х
х
имеет координаты
![]() .
Тогда имеем
.
Тогда имеем
![]() и
и
![]()
В координатной форме полученное векторное равенство имеет вид
 или
или
 .
(2)
.
(2)
Формулы (2)
представляют собой формулы перехода
от “старой“ системы координат Оху
к “новой“
системе координат
![]() и наоборот.
и наоборот.
Пример 5.
Получить уравнение окружности
![]() выполнив параллельный перенос системы
координат в
центр окружности.
выполнив параллельный перенос системы
координат в
центр окружности.
И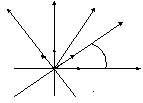 з
формул (2) следует
з
формул (2) следует![]()
![]() у
у
2.
Поворот системы координат.
![]() М
М
Рассмотрим две
системы координат
![]()
с общим началом, но с различными
направлениями
осей. В системе коор-
![]()
![]()
![]()
![]()
динат Оху
вектор
![]() ,О
,О
![]() х
х
а в системе
координат
![]() вектор
вектор
![]() .
.
Разложим векторы
![]() по базису
по базису![]() :
:
Тогда имеем
![]() ,
,
откуда, переходя к координатной форме, получим формулы перехода
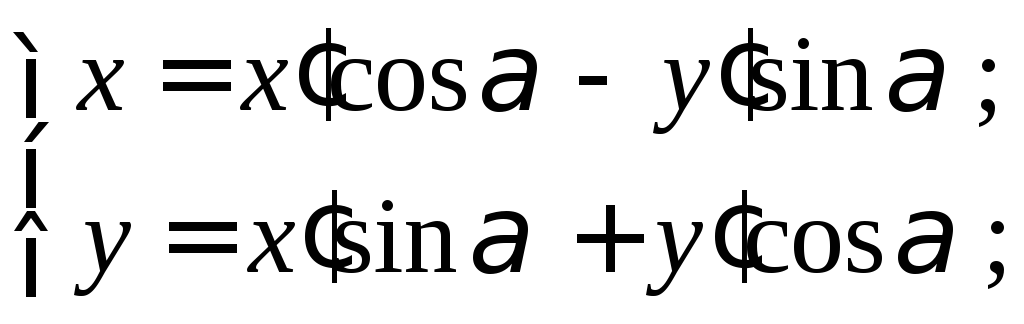 (3)
(3)
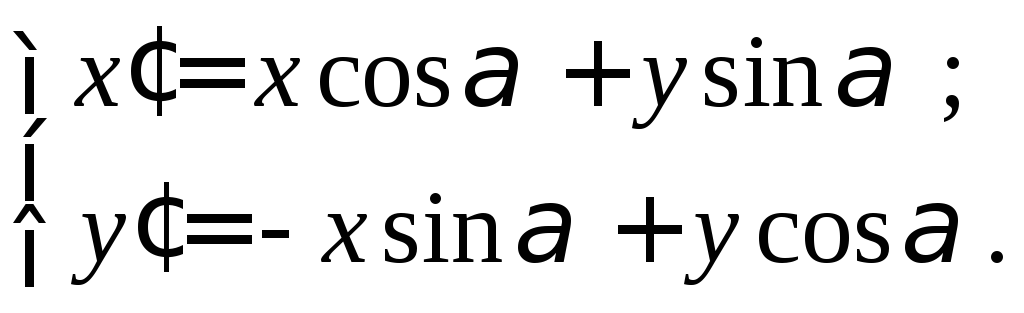 (4)
(4)
Формулы (3)
представляют собой переход от “старой“
системы координат Оху
к “новой“ системе
![]() ,
а формулы (4) – наоборот.
,
а формулы (4) – наоборот.
Пример 6.
Составить уравнение гиперболы
![]() при повороте системы координат на угол
при повороте системы координат на угол![]() .
.
Используя формулы
(3), получаем
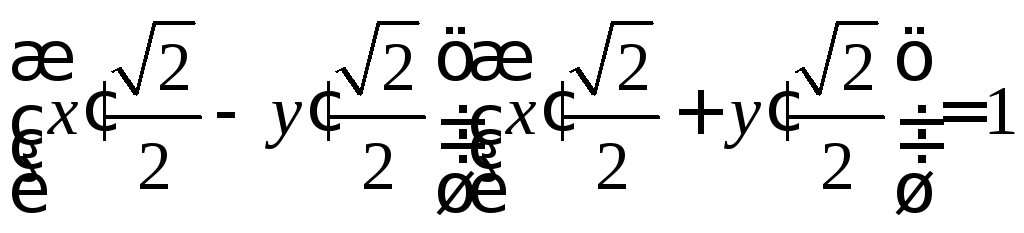
или
 (каноническое уравнение гиперболы).
(каноническое уравнение гиперболы).
3. Общий случай: поворот вместе с параллельным переносом осущест-вляется согласно формулам (2) и (3):
 (5)
(5)
Для того, чтобы
получить уравнение линии
![]() в новой системе координат, необходимо
в это уравнение подставить формулы
(5).
в новой системе координат, необходимо
в это уравнение подставить формулы
(5).
Лекция № 8. Тема 2 : Прямая линия на плоскости
2.1. Уравнения прямой линии
Теорема.
В ДСК на плоскости каждая прямая линия
может быть задана линейным уравнением
и наоборот, т.е. любое уравнение вида
![]() в ДСК определяет на плоскости прямую
линию.
в ДСК определяет на плоскости прямую
линию.
П усть
усть![]() – нормальный вектору
– нормальный вектору
прямой (вектор
перпендикулярный прямой)
![]()
и точка
![]() принадлежит данной
принадлежит данной![]()
прямой. Если
![]() - текущая точка
- текущая точка![]()
прямой, тогда для всех точек
прямой выполняется равенство О х
![]() (1)
(1)
Уравнение (1) является уравнением первой степени.
Обратно. Пусть
дано линейное уравнение и пусть точка
![]() принадлежит линии, которая определена
этим уравнением. Тогда получаем равенства:
принадлежит линии, которая определена
этим уравнением. Тогда получаем равенства:
![]()
Вычитая их последовательно, имеем
![]()
Если ввести
обозначение
![]() – нормальный вектор, то полученное
уравнение (1) будет определять прямую
линию. После раскрытия скобок получаем
уравнение
– нормальный вектор, то полученное
уравнение (1) будет определять прямую
линию. После раскрытия скобок получаем
уравнение![]() которое называетсяобщим
уравне-нием прямой.
которое называетсяобщим
уравне-нием прямой.
З амечание
1. Из
доказательства теоремы следует, что
вектор
амечание
1. Из
доказательства теоремы следует, что
вектор
![]() является нормальным вектором прямой.у
является нормальным вектором прямой.у
Кроме того, прямая
может быть
![]()
определена, если
будет задана точка
![]()
![]() ,
принадлежащая прямой
,
принадлежащая прямой
![]()
и вектор
![]() ,
которому она
,
которому она
параллельна (направляющий вектор). О х
Пусть точка
![]()
текущая точка прямой. Из коллинеарности
векторов
текущая точка прямой. Из коллинеарности
векторов
![]() и
и![]() следует равенство
следует равенство
![]() (2)
(2)
Уравнение (2) называется векторным параметрическим уравнением прямой. Переходя к координатной форме, получим
 (3)
(3)
Уравнения (3) называются параметрическими уравнениями прямой. Если исключить из них параметр t, то приходим к уравнению прямой с угловым коэффициентом (или приведенное уравнение прямой)
![]() (4)
(4)
![]()
 y
y
который образует прямая с осью Ох; b
![]()
![]()
прямой на оси Оу. O x
Замечание 2. Если прямая параллельна оси Оу, то её уравнение имеет вид х = х0 (в этом случае т = 0). Если – оси Ох, то у = у0 (п = 0).
