Міністерство освіти і науки, молоді та спорту України

Полтавський національний технічний університет

імені Юрія Кондратюка

Кафедра вищої математики

Методичні вказівки

до практичних занять за темою

«Основні методи інтегрування»

Полтава 2012

Методичні вказівки до практичних занять за темою «Основні методи інтегрування» з дисципліни «Вища математика» для студентів напряму підготовки 6.060101 «Будівництво». —Полтава: ПолтНТУ, 2012. — 26 с.

Укладачі: Л.М. Блажко, к.ф.–м.н., доцент, І.В. Рассоха, ст. викладач.

Відповідальний за випуск: Cєров М.І., завідувач кафедри вищої математики, доктор фізико–математичних наук, професор.

Рецензент: Сєрова М.М.., к.ф.–м.н., доцент.

Затверджено науково-методичною

радою університету

від 01.06.2012 р., протокол № 9

26.07.05.05

Багато практичних задач приводять до завдання: для заданої функції знайти таку функцію , похідна якої дорівнювала б , тобто

Таку операцію називають операцією інтегрування.

Зазначимо, що немає універсального методу інтегрування функцій, проте існують класичні, або основні, методи інтегрування, до яких належать: метод безпосереднього інтегрування, метод лінійного аргументу, метод підведення під знак диференціалу, метод заміни змінної та метод інтегрування частинами.

Надалі будуть використовуватись таблиця невизначених інтегралів та найпростіші правила інтегрування.

Таблиця невизначених інтегралів

1) 7)

8)

9)

10)

2) 11)

3) 12)

4) 13)

5) 14)

6)

Найпростіші правила інтегрування:

1.Якщо а – постійна, то: .

2. .

3.Якщо ,то .

при .

при .

4.Якщо і - диференційована функція, то

Основні методи інтегрування

Безпосереднє інтегрування

Обчислення невизначеного інтеграла з використанням таблиці інтегралів та властивостей інтегралів називається безпосереднім інтегруванням. Часто при цьому виконують тотожні перетворення підінтегральної функції, щоб звести інтеграл до табличного.

Приклади:

1)

2)

3)

4)

5)

6)

Метод лінійного аргументу

Базується на використанні властивості .

Приклади:

1)

2)

3)

Метод підведення під знак диференціала

Даний метод базується на властивості невизначених інтегралів. Вона означає, що вигляд формули інтегрування залишається незмінним незалежно від того, чи є змінна інтегрування незалежною змінною, чи деякою диференційованою функцією (інваріантність формул інтегрування).

Отже, якщо:

, то

Метод підведення під знак диференціала в багатьох випадках дозволяє зводити інтеграли до табличних.

Приклади:

1.

Функцію у цьому випадку вважаємо . Цю функцію підводимо під знак диференціала:

,

Тоді

2.

Підводимо під знак диференціала вираз , і враховуючи, що , , маємо:

3.

Під знак диференціала підводимо функцію , тоді , отже,

При використанні табличних формул необхідно уважно слідкувати за тим, щоб у нас була не тільки підінтегральна функція, а і диференціал тієї функції, яку потрібно вибрати в якості нової змінної інтегрування.

Метод заміни змінної

В основі інтегрування шляхом заміни змінної або підстановки лежить наступна формула: якщо то

Функцію потрібно вибирати так, щоб можна було невизначений інтеграл, розташований у правій частині цієї нерівності, звести то табличного. Вирахуємо, наприклад, інтеграл:

1)

Так як ,тоді перетворимо:

Залишається лише повернутися до змінної , підставляючи замість :

При виборі підстановки , спрощується підінтегральний вираз, необхідно пам’ятати, що у його складі повинен знайтися множник .

При деякій навичці у виконанні підстановки можна самої змінної не писати. Наприклад, в інтегралі:

в думках розглядають як нову змінну і відразу переходять до результату. Такий спосіб перетворення підінтегрального виразу називають внесенням функції під знак диференціала, який розглянуто раніше.

Наведемо інші приклади:

2)

.

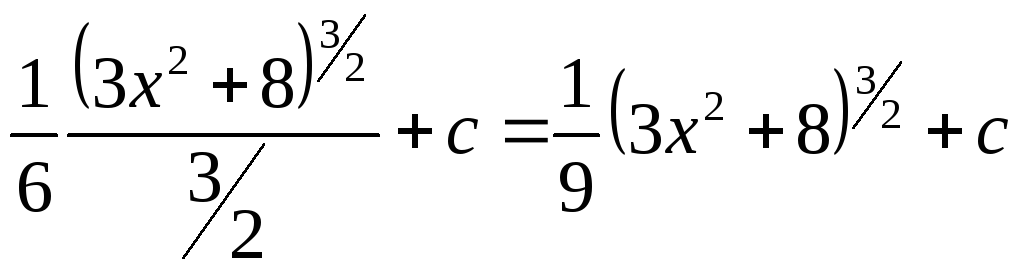3)

Вміння розшукувати потрібні підстановки та підносити під знак диференціала виробляється в результаті вправ. Потрібну інформацію, що полегшує цей пошук, можна знайти в даній таблиці:

№	Вид інтеграла	Підстановка	Внесення під знак диференціала	Новий вид інтеграла
1
2
3
4
5
6
7
8
9
10
11
12

Метод інтегрування за частинами

Застосування формули

Для знаходження первісної називається інтегруванням за частинами.

До інтегрування за частинами відносяться випадки, коли підінтегральний вираз містить:

а) вид , , , ;

б) логарифмічні функції;

в) зворотні тригонометричні функції;

г) деякі інші функції;

Щоб застосувати формулу інтегрування за частинами, треба увесь підінтегральний вираз розбити на два множника, один із яких позначити , а другий - При цьому:

1) повинен бути віднесений до ;

2) повинен бути таким, щоб інтегруванням можна було легко знайти , так як (константу не додавати!).

Для випадків, перерахованих в пунктах а, б і в, можна користуватися наступним правилом: за потрібно брати таку функцію, із підінтегрального виразу, яка при диференціюванні спрощується, а інша частина – має відомий інтеграл.

Застосовуючи формулу інтегрування за частинами, ми не відразу знаходимо первісну, а заданий інтеграл приводимо до іншого і якщо цей інтеграл легше заданого чи табличний, то формула застосована вірно.

Розглянемо приклади:

1)

Розбиваємо підінтегральний вираз на множники , .

Знаходимо

.

Всі знайдені вирази підставляємо у формулу інтегрування за частинами:

;

Останній інтеграл – табличний

Коротке розв’язання даного прикладу можна оформити наступним чином:

Іноді інтегрування за частинами доводиться застосовувати декілька разів, одержаний інтеграл знову інтегрується за частинами. Наприклад:

2) Отриманий інтеграл простіший заданого (замість тут ), але містить розв’язок тих самих функцій, отже , необхідно застосовувати той же спосіб інтегрування. Розподіляємо множники і застосовуємо формулу інтегрування за частинами.

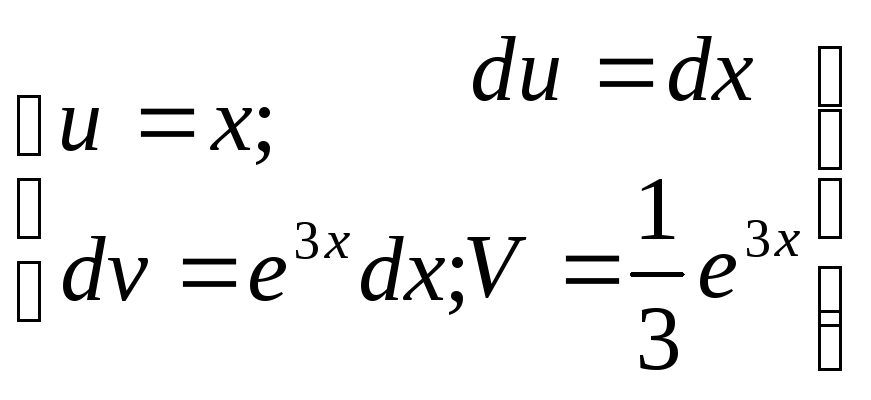
3)

Так як жодна із підінтегральних функцій і при диференціюванні не спрощується, то неважливо, яку із функцій прийняти за .Зробимо, наприклад, так:

Інтеграл, отриманий з правої частини, аналогічний заданому. Отже, його знову інтегруємо за частинами. Але тепер і треба вибирати так, як було вибрано при першому інтегруванні. А саме:

Перепишемо:

В правій і лівій частинах рівності маємо однакові інтеграли. Переносимо останній член в ліву частину рівності:

,

Звідки знаходимо остаточно:

.

Наведемо таблицю, яка полегшує вибір співмножників при інтегруванні частинами .

№	Вид інтеграла	Співмножник	Співмножник
1	де - многочлен
2
3		Можливий будь-який вибір співмножників
4
5