Компьютерная графика ч1

32

Кривые Безье

В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно).

Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 8). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.

Обозначим опорные точки как Pi ,i 0,2 , начало кривой положим в точке P0 (t=0), а конец

					в точке P2	(t=1), для каждого t [0,1] найдем
					точку P2
					0
					P01 (1 t)P0 tP1
					P11 (1 t)P1 tP2
					P2 (1 t)P1			tP1
	Рис. 1. Кривая Безье с 3 опорными				0		0	1		,
					(1 t)2 P0		2t(1 t)P1 t2 P2
		точками.
					таким образом, получим кривую второго
					порядка.
	Теперь построим аналогичным методом кривую Безье с 4 опорными точками.
							P01 (1 t)P0 tP1
							P11 (1 t)P1 tP2
							P21 (1 t)P2 tP3
							P2 (1 t)P1			tP1
								0	0	1
								(1 t)2 P0 2t(1 t)P1 t2 P2
						P2	(1 t)P1		tP1
						1		1	2
						(1 t)2 P1 2t(1 t)P2 t2 P3
	Рис. 2. Кривая Безье с 4 опорными точками.
	P3	(1 t)P2	tP2	(1 t)2P2	2t(1 t)P2	t2P2
	0	0	1	1	1		1

(1 t)3 P0 3t(1 t)2 P1 3t2 (1 t)P2 t3 P3

Кривые Фергюсона

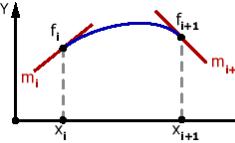
Рис. 3. Кубическая интерполяция Эрмита.

33

Пусть заданы следующие условия:

f(xi ) fi
f(xi 1 ) fi 1
	,i 0, N 1
f'(xi ) mi

f'(xi 1 ) mi 1

тогда для каждого i будем искать искомую

функцию в виде a*x3 b*x2 c*x d . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно.

Класс C1

Лабораторные основы

Цель работы: программно проиллюстрировать свойства кривых Безье и Фергюсона. Основные понятия, используемые в лабораторной работе: Явный,

неявный и параметрический вид задания функции. Представление контуров в машинной графике. Переход от представления контура в виде параметрической кубической кривой к кусочно-линейному представлению.Кривые в форме Безье. Кривые в форме Фергюсона.

Последовательность выполнения лабораторной работы

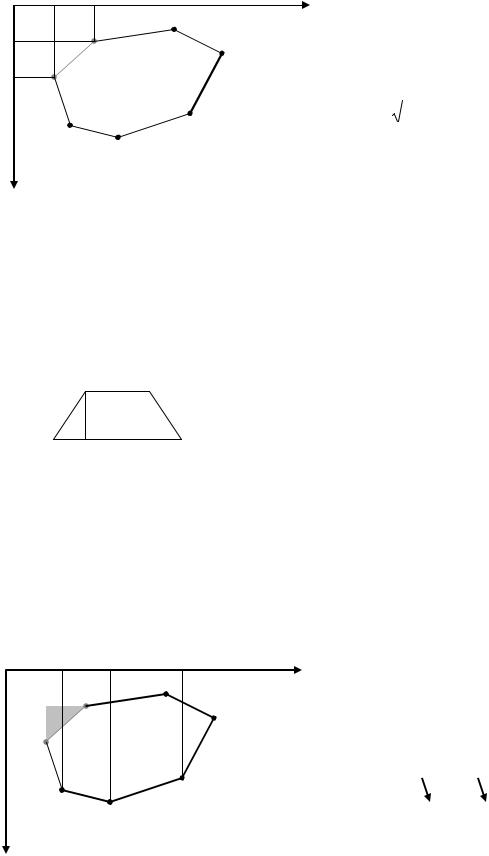
Задание 1. Нарисовать произвольно расположенные 4 точки - опорные точки для кривой Безье.

Задание 2. Последовательно соединить полученные 4 точки. Получим замкнутый контур, две стороны которого - будущие касательные для кривой Безье.

Задание 3. На форме заготовлены 4 метки: РО, PI, P2, РЗ, которые надо программно установить у одноименных точек. Для размещения метки на форме у определенной точки учтем, что,например, Х-координата метки РО - это свойство PO.Left, Y-координата - это свойство РО.Тор. В этом задании мы как бы развесим флажки на наши точки - "гвоздики", вбитые в форму для натяжения контура для кривой Безье.

Задание 4. Вписать в процедуру "Кривая Безье" параметрические формулы кривой Безье для координат X и Y .

Задание 5. Включить часы установкой свойства таймера Enabled.

Задание 6. Дописать цикл в процедуре для таймера, чтобы увидеть во времени построение кривой Безье.

Задание 7. Обратить внимание на работу процедуры FormMouseMove: вслед за движением мыши перемещается точка Р1 и, как следствие, перестраивается контур, а за ним и динамически перерисовывается кривая Безье.

34

Лабораторная работа № 3:

Часть 1"Вычисление площади и периметра произвольного многоугольника"

Математические основы

Периметр

Периметром многоугольника называется сумма длин его сторон. В основу нахождения периметра многоугольника заложена теорема Пифагора.

0	xi	xi+1	х
yi+1			Ti=(xi, yi), где i=1, …, N
yi
			N 1
			P (xi 1 xi )2 ( yi 1 yi )2
			i 1

у

Многоугольник называется выпуклым, если он расположен по одну сторону от любой своей стороны, неограниченно продолженной.

Площадь

Трапецией называется четырёхугольник, две противоположные стороны которого параллельны, а две другие нет. Параллельные стороны называются основаниями.

b

	h	S	1	h(a b)
			2
		a

Метод трапеций для расчета площади многоугольника, представленного кусочно-линейным описанием

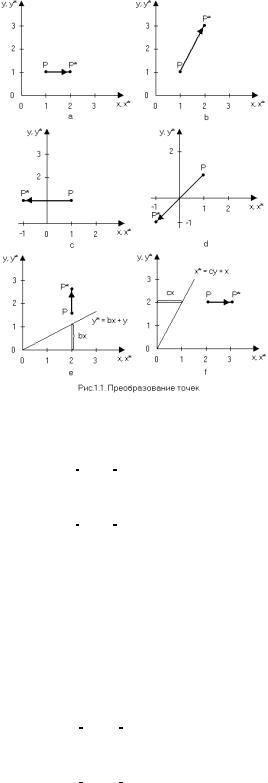
Суть метода заключается в том, что из вершин многоугольника выставляются перпендикуляры на ось х, образуя таким образом трапеции. Далее вычисляют площади этих трапеций. Одновременно при этом происходит вычитание "внешних площадей" (с момента, когда координаты по х начинают идти в обратную сторону), что приводит к вычислению истинной площади многоугольника.

0	xi		xi+1			х
yi+1						Ti=(xi, yi), где i=1, …, N
yi						N 1
						S 0,5 (xi xi 1)( yi yi 1)
						i 1
						h	a+b

у

35

Лабораторные основы

Цель работы: изучить способы вычисления площади и периметра замкнутых плоских деталей, представленных кусочно-линейным описанием.

Суть работы заключается в том, что в области рисования выставляются мышкой вершины многоугольника, координаты которых записываются в массив. Далее необходимо отобразить многоугольник, выставить перпендикуляры для наглядности и подсчитать площадь и периметр многоугольника. В конце работы необходимо доказать правильность расчётов.

Часть 2"Геометрические преобразования. Сдвиг, масштабирование, поворот, симметрия"

Математические основы

Двумерные преобразования

Преобразование точек

Точка представляется на плоскости двумя своими координатами, которые определяются как элементы матрицы размером 1х2 [х у]. В трехмерном пространстве используется матрица размером 1х3 [x у z]. Иначе говоря, точка может задаваться в виде вектор-столбца

x y

в двумерном пространстве или в виде

x y z

в трехмерном. Строку [х у] или столбец часто называют координатным вектором. Для формирования такого вектора используется матрица-строка, т. е. множество точек, каждая из которых определяет координатный вектор в некоторой системе измерения. Данное множество хранится в виде матрицы или массива чисел. Положением точек можно управлять путем манипулирования соответствующей матрицей. Линии, соединяющие точки, формируют отрезки, кривые и картинки.

В качестве элементов матрицы могут фигурировать различные величины: числа, сетки или коэффициенты системы уравнений. Правила в матричной алгебре определяют допустимые операции над элементами. Многие физические задачи удобно выражаются в

36

матричном представлении. Для моделей физических систем задача обычно ставится следующим образом: даны матрицы [А] и [В], найти результирующую матрицу [Т], такую, что [А][Т] = [В]. В этом случае решением является матрица [Т] = [А]-1[В], где [А]-1 - матрица, обратная к квадратной матрице [А].

В то же время матрицу [Т] можно интерпретировать как геометрический оператор. В этом случае для выполнения геометрического преобразования точек, представленных векторами положений в матрице [А], используется умножение матриц. Предположим, что матрицы [А] и [T] известны. Требуется определить элементы матрицы [В]. Представление [T] как геометрического оператора является основой математических преобразований, используемых в машинной графике.

Рассмотрим результаты умножения матрицы [х у], содержащей координаты точки Р, на матрицу общего преобразования размером 2х2:

[X][T] = [x y]	a	b	[(ax + cy) (bx + dy)]
	c	d

Данная запись означает, что исходные координаты точки х и у преобразуются в х* и y*, где где х* = ах + су, у* = bх + dy. Представляют интерес значения х*, у* - координаты результирующей, преобразованной точки Р. Рассмотрим некоторые специальные случаи.

При а = d = 1 и с = b = 0 преобразование сведется к единичной матрице

[X][T] = [x y]	1	0	[x y] = [x* y*]
	0	1

и координаты точки Р останутся неизменными. Как и следовало ожидать, в линейной алгебре умножение на единичную матрицу эквивалентно умножению на 1 в обычной алгебре.

В случае d = 1, b = c = 0

[X][T] = [x y]	а	0	[аx y] = [x* y*]
	0	1

где х* = ах - результат масштабирования координаты х. Эффект показан на рисунке

1.1,а.

37

Рассмотрим теперь еще случай b = с = 0, т.е.

[X][T] = [x y]	а	0	[аx yd] = [x* y*]
	0	d

Данное преобразование вызывает изменение обеих координат х и у вектора Р (рис. 1.1,b). Если а <> d, то координаты масштабируются различным образом. При a = d > 1 происходит растяжение вектора Р или масштабирование координат. Если 0 < а = d < 1, то имеет место сжатие.

Если значение а или d отрицательное, то вектор отражается относительно координатных осей или относительно плоскости. Чтобы убедиться в этом, возьмем b = c = 0, d = 1 и а = 1, тогда

[X][T] = [x y]	-1	0	[-x y] = [x* y*]
	0	1

и в результате получаем симметричное отражение относительно оси y (рис. 1.1,c). Если b = c = 0, а = 1, d = -1, то выполняется симметричное отражение относительно оси х. Если b = с = 0, а = d < 0, то происходит отражение относительно начала координат, это показано на рисунке 1.1,d, где a = -1, d =1. Заметим, что обе операции отражения и масштабирование зависят только от диагональных членов матрицы преобразования.

Рассмотрим теперь случай с недиагональными членами. Возьмем сначала значения a = d = 1, c = 0, тогда

			38
[X][T] = [x y]		b		[x (bx + y)] = [x* y*]
	1
	0	1

Заметим, что координата х точки Р осталась неизменной, тогда как координата y линейно зависит от исходных координат. Данное преобразование называется сдвигом (рис. 1.1,e). Аналогично, в случае, когда а = d = 1, b = 0, преобразование приведет к сдвигу пропорционально координате y (рис. 1.1,f). Таким образом, видно, что недиагональные члены матрицы преобразования создают эффект сдвига координат вектора точки Р.

Прежде чем закончить с преобразованием точек, разберем действие общего преобразования, когда начальный вектор лежит в точке начала координат, т.е.

[X][T] = [x y]	a	b	[(ax + cy) (bx + dy)]
	c	d

или в случае начала координат,

[X][T] = [0 0]	a	b	[0 0] = [x* y*]
	c	d

Видно, что начало координат инвариантно относительно преобразования общего вида. Это ограничение устраняется при использовании однородных координат.

Преобразование параллельных линий

Прямую линию можно определить с помощью двух векторов, задающих координаты ее конечных точек. Расположение и направление линии, соединяющей две эти точки, может изменяться в зависимости от положения векторов.

Результатом преобразования двух параллельных линий с помощью (2х2)-матрицы снова будут две параллельные линии. Это можно увидеть, рассмотрев линию между точками [А] = [x1 y1], [В] = [х2 y2] и параллельную ей линию, проходящую между точками E и F. Покажем, что для этих линий любое преобразование сохраняет параллельность. Так как АВ, EF и A*B* и E*F* параллельны, то угол наклона линий АВ и EF определяется следующим образом:

y2 - y1

m =

x2 - x1

Преобразуем конечные точки АВ, воспользовавшись матрицей общего преобразования размером (2х2):

39

A

[T] =

x1 y1

a b

=

ax1 + cy1 bx1 + dy1

=

x1* y1*

=

A*

B

x2 y2

c d

ax2 + cy2 bx2 + dy2

x2* y2*

B*

Наклон прямой А*В* определяется следующим образом:

	(bx2 + dy2) - (bx1 + dy1)	b(x2 - x1) + d(y2 - y1)
m* =		=
	(ax2 + cy2) - (ax1 + cy1)	a(x2 - x1) + c(y2 - y1)

или

(y2 - y1)

	b + d
	(x2 - x1)				b + dm
m* =				=
	(y2 - y1)				a + cm
	a + c
	(x2 - x1)

Так как наклон m* не зависит от х1, х2, y1, y2, а m, а, b, с и d одинаковы для EF и AB, то m* одинаково для E*F* и А*В*. Таким образом, параллельные линии сохраняют параллельность и после преобразования. Это означает, что при преобразовании (2х2) параллелограмм преобразуется в другой параллелограмм. Эти тривиальные выводы демонстрируют большие возможности использования матрицы преобразования для создания графических эффектов.

Преобразование пересекающихся прямых

Результатом преобразования с помощью (2х2)-матрицы пары пересекающихся прямых линий также будет пара пересекающихся линий. Проиллюстрируем это на примере двух прямых, заданных уравнениями:

y = m1x + b1

y= m2x + b2

Вматричном представлении эти уравнения будут иметь вид:

[X][T] = [x y]	-m1 -m2		= [b1 b2]
	1	1

или

[X][M] = [B]

40

Если существует решение этой системы уравнений, то линии пересекаются, в противном случае они параллельны. Решение можно найти путем инверсии матрицы. В частности,

[Xi] = [xi yi] = [B][M] -1

Матрица, обратная [М], имеет следующий вид:

1

m2 - m1

-1

m2 - m1

m2

m2 - m1 -m1

m2 - m1

так как [M][M] -1 = [E], где [E] - единичная матрица. Поэтому координаты точки пересечения двух линий можно найти следующим образом:

		1			m2
			m2 - m1
[Xi] = [xi yi] = [b1 b2]					m2 - m1
		-1			-m1
			m2 - m1		m2 - m1

	b1 – b2		b1m2 - b2m1
[Xi] = [xi yi] =
	m2 - m1		m2 - m1

Если обе линии преобразовать с помощью (2х2)-матрицы общего преобразования

вида:

[T] =	a	b
	c	d

то их уравнения будут иметь вид

y* = m1*x* + b1* y* = m2*x* + b2*

Соответственно можно показать, что

b + dmi

mi* =

a + cmi

41

и

	ad - bc
bi* = bi(d - cmi*) = bi			где i = 1, 2.
	a + cmi

Точка пересечения линий после преобразования отыскивается таким же образом, что и в случае исходных линий:

b1* - b2* b1*m2* - b2*m1* [Xi*] = [xi* yi*] =

m2* - m1* m2* - m1*

Воспользовавшись тремя предыдущими выражениями, получим:

	a(b1 - b2) + c(b1m2 – b2m1)		b(b1 - b2) + d(b1m2 - b2m1)
[Xi*] = [xi* yi*] =
	m2 - m1		m2 - m1
Возвращаясь теперь к точке пересечения [xi yi] исходных линий и применяя уже
полученную матрицу преобразования, имеем

[xi* yi*] = [xi yi][T] =

b1

– b2 b1m2

- b2m1

a

b

=

c

d

m2 - m1 m2 - m1

a(b1 - b2) + c(b1m2 – b2m1)

b(b1 - b2) + d(b1m2 - b2m1)

=

m2 - m1

m2 - m1

Сравнение уравнений точек пересечения исходных линий и преобразованных показывает, что они одинаковы. Итак, точка пересечения преобразуется точно в другую точку пересечения.

Поворот

Рассмотрим треугольник ABC (рис.1.2) и с помощью следующего преобразования повернем его на 90° против часовой стрелки относительно начала координат

	T] =	1
		-1 0