Компьютерная графика ч1

52

1. Матрица сдвига

		1	0	0	0
	[T] =	0	1	0	0
		0	0	1	0
		d x	d y	d z	1

	2.	Матрица масштабирования
			sx	0	0	0
	[D] =		0	s y	0	0
			0	0	sz	0
			0	0	0	1
	3. Матрицы поворота на угол α
		cos		sin	0	0		1	0	0	0		cos	0	sin	0
[Roz] =	sin			cos	0	0	[Rox] =	0	cos	sin	0	[Roy] =	0	1	0	0
		0		0	1	0		0	sin	cos	0		sin	0	cos	0
		0		0	0	1		0	0	0	1		0	0	0	1

	4.		Матрицы симметрии
		1	0	0	0		1 0		0	0		1	0	0	0
	[Mxy] =	0	1	0	0	[Myz] =	0	1	0	0	[Mzx] =	0	1 0		0
		0	0	1 0			0	0	1	0		0	0	1	0
		0	0	0	1		0	0	0	1		0	0	0	1

53

Лабораторная работа № 4

Часть 1"Аппроксимация. Mметод наименьших квадратов. Интерполяция. Метод Лагранжа."

Математические основы

Интерполяция - построение кривой, проходящей через контрольные точки. Аппроксимация - приближение кривой (не обязательно проходит точно через данные

точки, но удовлетворяет некоторому заданному свойству относительно этих точек).

Интерполяция

Постановка задачи:

Дано: f(xi) fi . xi xi 1 i

0, N . Построить функцию f(x), удовлетворяющую этому условию.

Рис. 4. Постановка задачи.

1) Интерполяционный многочлен Лагранжа

			N			N
N	N	N	(x xj)	N		(x xj)	N	j
			j 0,j i			j 0,j i
LN(x) fi Li		(x) fi		; Li	(x)		; Li	(xj) δi
			N			N
i 0		i 0	(xi xk )			(xi xk )
			k 0,k i			k 0,k i

Получаем непрерывную функцию, проходящую через все точки.

Минусы:

1)Требует значительного объема вычислений для нахождения значения функции

впроизвольной точке.

2)Неопределенное поведение построенной функции между узлами, в частности можно привести следующие результаты:

1916 Бернштейн : LN(x) 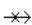x, N

1925 Рунге : LN(x) 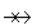1 25x2 1 C , N

Далее будем рассматривать интерполирующие функции, которые задаются отдельно на каждом отрезке [xi ,xi 1 ],i 0, N 1, что позволяет лучше учитывать локальное поведение

требуемой функции и избежать громоздких вычислений (так как на каждом из отрезков интерполирующая функция имеет по возможности простой вид).

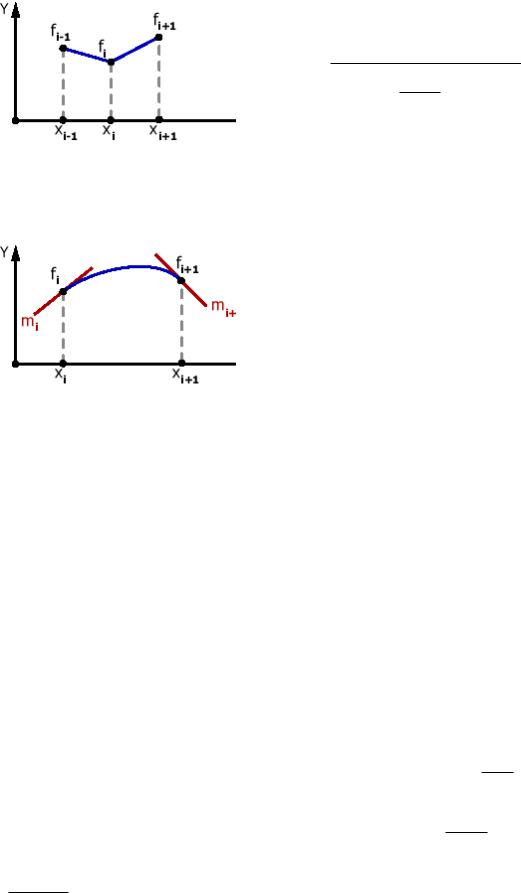
2) Кусочно-линейная интерполяция

54

Интерполяция следующей кусочнолинейной функцией:

f(x) fi 1 * (x xi ) fi * (x xi 1 ) , xi 1 xi

x [xi , xi 1 ],i 0, N 1

Класс C0

Рис. 5. Кусочно-линейная интерполяция.

3) Кубическая интерполяция Эрмита

Рис. 6. Кубическая интерполяция Эрмита.

Пусть заданы следующие условия:

f(xi ) fi
f(xi 1 ) fi 1
	,i 0, N 1
f'(xi ) mi

f'(xi 1 ) mi 1

тогда для каждого i будем искать искомую

функцию в виде a*x3 b*x2 c*x d . Подставив эту функцию в уравнения условий получим линейную невырожденную систему из 4 уравнений с 4 неизвестными (a,b,c и d), т.е. решение существует и единственно.

Класс C1

Проблемы:

1)Хотелось бы C2 , а не только C1

4)Сплайны

Сплайн - кусочный полином степени K с непрерывной производной степени K-1 в точках соединения сегментов.

Далее нас будут интересовать кубические сплайны.

Понятие сплайна пришло из машиностроения, где сплайном называли гибкую линейку, закрепив которую в нужных местах, добивались плавной кривой, которую затем чертили по этой линейке (см. Рис. 7) Форма такой линейки, если ее рассматривать как

функцию y(x), будет удовлетворять уравнению Эйлера-Бернулли: y''(x) M(x) ,где M(x) -

E*I

момент изгиба вдоль рейки, E - модуль Юнга. зависящий от свойств материала рейки, I - момент инерции, определяемый формой кривой. Если мы фиксируем некоторые точки

подпорками, то момент изгиба на каждом отрезке [xi ,xi 1 ],i 0, N 1 меняется по линейному закону: M(x) = A*x + B , подставляя в исходное уравнение получаем:

y''(x) A * x B , дважды интегрируя получаем уравнение кривой на данном

E*I

55

отрезке: y(x) a*x3 b*x2 c*x d ; таким

образом форма физического сплайна описывается кусочным кубическим полиномом.

Теперь рассмотрим задачу построения системы таких кубических полиномов для всего отрезка [x0 ,xN ]

Рис. 7. Сплайн.

1)Для N отрезков имеем 4N коэффициентов: y(x) ai *x3 bi *x2 ci *x di, для

x[xi ,xi 1 ],i 0, N 1;

2)Условия f(xi) fi( i 0, N ) дают 2N уравнений;

3)Требование C1 в точках xi ( i 1, N 1 ) дает N-1 уравнений;

4)Требование C2 в точках xi ( i 1, N 1 ) дает N-1 уравнений.

Итого имеем 4N-2 уравнения; для того чтобы система была определенной, необходимы еще 2 уравнения; их можно вывести, например, из заданных значений производных на границах или из условия периодичности. При корректно заданных условиях

линейная относительно ai, bi,ci, di,i 0, N 1 система имеет единственное решение.

Аппроксимация

1) Кривые Безье

В настоящее время для задач аппроксимации наиболее широко применяются кривые Безье. Это связано с их удобством как для аналитического описания, так и для наглядного геометрического построения (применительно к компьютерной графике это означает, что пользователь может задавать форму кривой интерактивно).

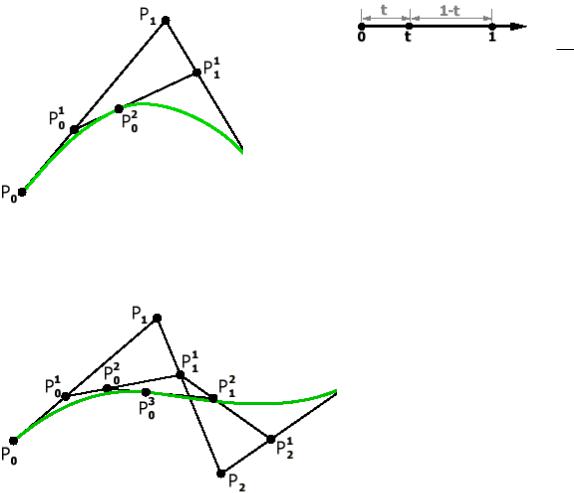
Наглядный метод построения этих кривых был предложен de Casteljau в 1959 году. Построим кривую по 3 опорным точкам (Рис. 8). Метод de Casteljau основан на разбиении отрезков, соединяющих исходные точки в отношении t (значение параметра), а затем в рекурсивном повторении этого процесса для полученных отрезков.

56

Обозначим опорные точки как Pi ,i 0,2 , начало кривой положим в точке P0 (t=0), а конец

					в точке P2	(t=1), для каждого t [0,1] найдем
					точку P2
					0
					P01 (1 t)P0 tP1
					P11 (1 t)P1 tP2
					P2 (1 t)P1			tP1
	Рис. 8. Кривая Безье с 3 опорными				0		0	1		,
					(1 t)2 P0		2t(1 t)P1 t2 P2
		точками.
					таким образом, получим кривую второго
					порядка.
	Теперь построим аналогичным методом кривую Безье с 4 опорными точками.
							P01 (1 t)P0 tP1
							P11 (1 t)P1 tP2
							P21 (1 t)P2 tP3
							P2 (1 t)P1			tP1
								0	0	1
								(1 t)2 P0 2t(1 t)P1 t2 P2
						P2	(1 t)P1		tP1
						1		1	2
						(1 t)2 P1 2t(1 t)P2 t2 P3
	Рис. 9. Кривая Безье с 4 опорными точками.
	P3	(1 t)P2	tP2	(1 t)2P2	2t(1 t)P2	t2P2
	0	0	1	1	1		1

(1 t)3 P0 3t(1 t)2 P1 3t2 (1 t)P2 t3 P3

Можно продолжать подобные построения и для большего числа узлов, получая аналогичные выкладки. Запишем общее аналитическое представление для кривой Безье с N+1 опорной точкой:

			n	n!
	Pn (t) Pi Bin (t) , где Bin (t) Cin ti (1 t)n i					ti (1	t)n i , где
				i!(n i)!
			i 0
Cn	n!		- биномиальные коэффициенты,
i	i!(n i)!

Bin (t) называются базисными многочленами Бернштейна n степени (а также весовыми функциями Безье/Бернштейна).

Лабораторные основы

Цель работы: изучить интерполяционный многочлен Лагранжа и научиться вычислять параметры для аппроксимирующих функций, чтобы строить графики зависимостей для произвольных наборов точек.

Основные понятия, используемые в лабораторной работе: Аппроксимация и интерполяция: различие и сходство. Метод наименьших квадратов. Многочлен Лагранжа.

57

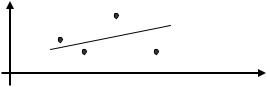
Под аппроксимацией обычно понимают операцию сглаживания, которая призвана уменьшить осцилляции, обусловленные неверными значениями некоторых координат. Задача аппроксимации возникает тогда, когда по заданному массиву точек [xi, yi], где i=0, 1, …, m, требуется построить функцию, проходящую не через заданные точки, а вблизи них, и изменяющуюся достаточно плавно.

δi	Аппроксимация: δi → min
	Интерполяция: δi = 0

Метод наименьших квадратов

Предположим, у нас имеется набор экспериментальных точек зависимости Y от X . Возникает вопрос, как по этим экспериментальным точкам наилучшим образом воспроизвести зависимость Y от X? Для решения подобных задач обычно применяется расчетный метод, известный под названием "Метод наименьших квадратов". Этот метод дает возможность при заданном типе зависимости Y=f(X) так выбрать ее числовые параметры, чтобы график зависимости Y=f(X) наилучшим образом отображал экспериментальные данные. Тип зависимости Y=f(X), как правило, выбирается исходя из внешнего вида полученного набора точек. Он может быть линейным, квадратичным, экспоненциальным и т.д. . В методе наименьших квадратов под условием «наилучшим образом» понимают следующее требование: "Сумма квадратов отклонений экспериментальных точек от сглаживающей кривой должна быть минимальной".

Рассмотрим линейную зависимость. Пусть имеется набор из n экспериментальных точек с координатами (х1, y1), (х2, у2), ..., (хn, уn). Предполагается, что точки отображают линейную зависимость. Требуется подобрать по методу наименьших квадратов коэффициенты а и b линейной функции у = ах + b.

Решение. Запишем у как функцию не только аргумента х, но и параметров а и b (так как величины а и b неизвестны ):

у = f (х; a, b) = ax + b

(1)

Требуется выбрать а и b так, чтобы выполнялось условие: "Сумма квадратов отклонений экспериментальных точек от построенной линейной зависимости должна быть минимальной", то есть для набора n экспериментальных точек должно быть выполнено условие :

n	2
yi	f (xi )	min (2)
i 1
или
n		2
yi	f (axi	b)	min

i 1

58

где уi - значение у-координаты i-ой точки из набора экспериментальных точек, хi - значение x-координаты i-ой точки из набора экспериментальных точек, (ахi + b) - значение функции у = ах + b в i-ой точке.

Найдём значения а и b, при которых левая часть выражения (2) обращается в минимум. Для этого продифференцируем её по а и b; приравняем производные нулю:

n

dy

n

dy

yi

y(xi

)

0 ;

yi

y(xi

)

0

(3)

i 1

da i

i 1

db i

dy

где - значение частной производной функции у(х) = ах + b по параметру а в

da i

dy

точке c координатами (хi, уi) , а - значение частной производной функции по

db i

параметру b.

Система уравнений (3) содержит столько уравнений, сколько неизвестных коэффициентов в искомой зависимости. В нашем случае их два – а и b. Продифференцируем

(1) по а и b, получим:

dy			d (ax b)	x		dy				xi
					;
da			da			da i
										(4)
dy			d (ax b)	1		dy				1
					;
db			db			db i

Подставим выражения (4) в (3) и получим два уравнения для определения а и b:

n
yi (axi	b) xi	0
i 1
		(5)
n
yi (axi	b) 1 0

i 1

Раскроем скобки, просуммируем и получим:

n	n	n
xi	yi a xi2 b xi		0	(6)
i 1	i 1	i 1
n	n
yi	a xi	bn 0 ,	где n – число точек
i 1	i 1

Получили систему из двух уравнений с двумя неизвестными, которая легко решается. Рассмотрим теперь конкретный пример. Пусть имеется набор из 3 экспериментальных точек с координатами (1,1), (2,2) и (3,0). Предполагается, что точки отображают линейную

			59
зависимость. Требуется найти коэффициенты а и b для линейной функции у = ах + b.
		Решение.
Xi		Уi	Воспользуемся системой уравнений (6) и подставим в неё координаты
			экспериментальных точек. Получаем следующую систему уравнений:
1		1
2		2	(1 1 2 2 3 0) a(12 22 32 ) b(1 2 3) 0
3		0	(1 2 0) a(1 2 3) b 3 0

14a 6b 5

2a b 1

Решаем и получаем a = -0.5, b = 2. Таким образом, вид линейной функции: у = - 0.5 х +

2 .

Под интерполяцией понимают построение гладкой функции, проходящей через все заданные точки. Для этого применяют интерполяционные кубические сплайны, NURBS-сплайны, B-сплайны и т.п.

Интерполяционный многочлен Лагранжа

Многочлен Лагранжа в основном используют для учебных целей, хотя его можно применять и на практике (в случае небольшого количества точек).

По заданному массиву точек (xi, yi), где i=0, 1,

Lm	…, m интерполяционный многочлен Лагранжа
	определяется формулой:

x0 x

xm

m

m'

m

Lm (x) yi

i 0

m

(x) (x xi )

i 0,i m

m

(xi ) (xm xi

i 0,i m

m (x)		,	где
(x xi ) m'
	(xi )

)

Рассмотрим конкретный пример. Распишем интерполяционный многочлен Лагранжа для трёх точек (i=0,…, 2): Lm (x) y0 L0 y1 L1 y2 L2

	L0			(x x1 ) (x x2 )
				(x0	x1 ) (x0 x2 )
	L1			(x x0 ) (x x2 )
			(x1		x0 ) (x1 x2 )
	L2			(x x0 ) (x x1 )
				(x2	x0 ) (x2 x1 )

60

Часть 2"Закраска произвольных областей"

Математические основы

Простой алгоритм заполнения с затравкой

В алгоритмах заполнения с затравкой предполагается, что известен хотя бы один пиксель из внутренней области многоугольника. Алгоритм пытается найти и закрасить все другие пиксели, принадлежащие внутренней области. Области могут быть либо внутренне-, либо гранично-определенными. Если область относится к внутренне-определенным, то все пиксели, принадлежащие внутренней части, имеют один и тот же цвет или интенсивность, а все пиксели, внешние по отношению к области, имеют другой цвет. Это продемонстрировано на рис. 2.12. Если область относится к гранично-определенным, то все пиксели на границе области имеют выделенное значение или цвет, как это показано на рис. 2.13. Ни один из пикселей из внутренней части такой области не может иметь это выделенное значение. Тем не менее пиксели, внешние по отношению к границе, также могут иметь граничное значение. Алгоритмы, заполняющие внутренне-определенные области, называются внутренне-заполняющими, а алгоритмы для гранично-определенных областей - гранично-заполняющими. Далее будут обсуждаться гранично-заполняющие алгоритмы, однако соответствующие внутренне-заполняющие алгоритмы можно получить аналогичным образом.

Внутреннеили гранично-определенные области могут быть 4-или 8-связными. Если область 4-связная, то любого пикселя в области можно достичь с помощью комбинации движений только в 4 направлениях: налево, направо, вверх, вниз. Для 8-связной области пикселя можно достичь с помощью комбинации движений в двух горизонтальных, двух вертикальных и 4 диагональных направлениях (рис. 2.14).

Далее речь в основном пойдет об алгоритмах для 4-связных областей, однако их можно легко переделать для 8-связных областей, если заполнение проводить не в 4, а в 8 направлениях.

61

Используя стек, можно разработать простой алгоритм заполнения граничноопределенной области. Стек - это просто массив или другая структура данных, в которую можно последовательно пометить значения и из которой их можно последовательно извлекать. Когда новые значения добавляются или помещаются в стек, все остальные значения опускаются вниз на один уровень. Когда значения удаляются или извлекаются из стека, остальные значения всплывают или поднимаются вверх на один уровень. Такой стек называется стеком прямого действия. Простой алгоритм заполнения с затравкой можно представить в следующем виде:

Простой алгоритм заполнения с затравкой и стеком.

Поместить затравочный пиксель в стек Пока стек не пуст Извлечь пиксель из стека Присвоить пикселю требуемое значение Для каждого из соседних к текущему 4-связных пикселей проверить: является ли он граничным пикселем или не присвоено ли уже пикселю требуемое значение. Проигнорировать пиксель в любом из этих двух случаев. В противном

случае поместить пиксель в стек.

Приведем более формальное изложение алгоритма, в котором предполагается существование затравочного пикселя и гранично-определенной области: Затравка(х, у) - выдает затравочный пиксель

Push - процедура, которая помещает пиксель в стек Pop - процедура, которая извлекает пиксель из стека

Пиксель х, у) = Затравка(х, у)
Push Пиксель х, у)	/ инициализируем
while (стек не пуст)	стек
Pop Пиксель х, у)	/ извлекаем пиксель
if Пиксель х, у) <> Нов_значение then	из стека
Пиксель х, у) = Нов_значение
end if

if (Пиксель х + 1, у) <> Нов_значение and

Пиксель х + 1, у) <> Гран_значение) then Push Пиксель (х + 1, у)

if (Пиксель х, у + 1) <> Нов_значение and Пиксель х, у + 1) <> Гран_значение) then Push Пиксель (х, у + 1)

if (Пиксель х - 1, у) <> Нов_значение and Пиксель х - 1, у) <> Гран_значение) then Push Пиксель (х - 1, у)

if (Пиксель(х, у — 1) <> Нов_значение and Пиксель х, у - 1) <> Гран_значение) then Push Пиксель (х, у - 1)

end if end while

Пример 2.3. Алгоритм заполнения многоугольника с затравкой. В качестве примера применения алгоритма рассмотрим гранично-определенную область, содержащую дыру. Она изображена на рис. 2.15.