
ЭВМ и ПУ. Лекция 03 0
.pdfЛекция 3.
Процесс обработки информации в ЭВМ. Архитектура ЭВМ. Двоичные переключательные схемы и узлы.
Физические реализации представления информации в ЭВМ.
Двоичные переключательные схемы и узлы.
Элементарная форма представления информации получается с помощью двухэлементного множества и слов над ним. Примером такого двухэлементного множества является множество булевских значений B = {0, 1}. Представление информации через последовательности булевских значений или термов является господствующим принципом в используемых в настоящее время вычислительных машинах. Переработка так представленной информации в вычислительных машинах может быть описана с помощью функций, которые оперируют булевскими значениями, их кортежами (двоичными словами) или последовательностями двоичных слов.
Таким образом, булевские функции дают основу для описания процессов обработки информации. Сложные операции над двоичными словами могут быть технически представлены через переключательные узлы и схемы, которые могут быть подходящим образом скомбинированы из простых "кирпичиков", которые соответствуют элементарным булевским функциям. Электрические переключатели, как они находят применение в вычислительных машинах, реализуют такие узлы и схемы. Они служат тем самым для технической реали зации булевских функций.
Нормальные формы булевских функций
Одну и ту же функцию можно представить различными булевскими те р- мами. Однако для целей обработки информации в ЭВМ необходимо, чтобы один булевский терм представлял одну функцию. Это достигается в случае представления его в однозначной нормальной форме. Если для представления булевской функции задана однозначная нормальная форма, то каждая функция имеет единственное представление в этой нормальной форме. Два различных терма в нормальной форме представляют тогда различные функции.
Таблица значений образует однозначную нормальную форму представления булевских функций – для каждой булевской функции существует одна таблица значений.
Теорема (булевская нормальная форма). Любая n-местная булевская функция f может быть представлена в дизъюнктивной нормальной форме
(DNF).
Терм представлен в дизъюнктивной нормальной форме (называемой так-
же адъюнктивной нормальной формой) DNF, если он есть 1 или 0 или имеет следующий вид:
(t1 ˅ ... ˅ tk),
причем термы tj имеют вид
(v1 ˄ ... ˄ vk),
1

а термы vj имеют вид xj или ¬xj. Этот вид можно выразить через описание синтаксиса терма в форме БНФ:
<дизъюнктивная_нормальная_форма> :: = <конъюнкция>{ ˅ <конъюнкция>}*|0|1|
<конъюнкция> :: = <атом>{ ˄ <атом>}* <атом> :: = {¬}<id>
Синтаксическая единица <id> означает булевские идентификаторы x1, …, xn.
Дополнительно потребуем, чтобы никакой терм ti не совпадал с термом tj (i ≠ j). Если булевские термы упрощаются до вида
(v1 ˄ ... ˄ vn),
то такое термовое представление называется также совершенной дизъюнктив-
ной нормальной формой.
Совершенная дизъюнктивная форма часто может быть еще упрошена. Если, например, в DNF встречаются термы вида
… ˅ (t1 ˄ ... ˄ ti-1 ˄ xi ˄ ti+1 ˄ ... ˄ tn) ˅ ...
˅ (t1 ˄ ... ˄ ti-1 ˄ ¬xi ˄ ti+1 ˄ ... ˄ tn) ˅ ...,
то эти термы по правилам булевской алгебры можно заменить на терм
… ˅ (t1 ˄ ... ˄ ti-1 ˄ ti+1 ˄ ... ˄ tn) ˅ ...
При применении этого правила могут возникнуть частичные подтермы следующего вида:
… ˅ (t1 ˄ t2) ˅ ... ˅ (t1) ˅ ...
которые можно заменить на терм
... ˅ (t1) ˅ ...
Если мы будем применять эти упрощающие правила повторно, пока это во з-
можно, то получим упрощенную дизъюнктивную нормальную форму. Если в конце концов остается только терм вида х ˅ ¬х, то его можно заменить на 1. Если булевская функция задана таблицей ее значений, то из нее можно фо р- мально вывести представление функции в DNF. что объясняется следующим примером.
Пример (нормальная форма трехместной булевской функции). Пусть функция f задана табл. 2.2.
x1 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
x2 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
x3 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
f(x1 , x2 , x3) |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
Таблица 2.2. Таблица значении функции f
Для f(x1 , x2 , x3) из табл. 2.2 получим схематически следующее термовое пред- |
|
ставление: |
|
(1 ˄ x1 ˄ x2 ˄ x3) |
˅ |
(0 ˄ ¬x1 ˄ x2 ˄ x3) |
˅ |
(1 ˄ x1 ˄ ¬x2 ˄ x3) |
˅ |
(0 ˄ ¬x1 ˄ ¬x2 ˄ x3) |
˅ |
(0 ˄ x1 ˄ x2 ˄ ¬x3) |
˅ |
2
(0 ˄ ¬x1 ˄ x2 ˄ ¬x3) |
˅ |
(0 ˄ x1 ˄ ¬x2 ˄ ¬x3) |
˅ |
(1 ˄ ¬x1 ˄ ¬x2 ˄ ¬x3).
При первом упрощении (опускание конъюнкционных выражений, содержащих 0) получается следующее термовое представление:
(1 ˄ x1 ˄ x2 ˄ x3) ˅ (1 ˄ x1 ˄ ¬x2 ˄ x3) ˅ (1 ˄ ¬x1 ˄ ¬x2 ˄ ¬x3).
Далее, опуская 1, получим следующую нормальную форму:
(x1 ˄ x2 ˄ x3) ˅ (x1 ˄ ¬x2 ˄ x3) ˅ (¬x1 ˄ ¬x2 ˄ ¬x3).
Применение заданных правил упрощения дает в итоге упрощенную дизъюнктивную нормальную форму
(x1 ˄ x3) ˅ (¬x1 ˄ ¬x2 ˄ ¬x3).
Обратим внимание на то, что (с точностью до перестановок идентификаторов и термов в конъюнкции) каждая булевская функция и каждый булевский терм обладают единственной совершенной дизъюнктивной нормальной формой.
Булевский терм, который построен с помощью трех операций A, V и также с помощью правил замены термов можно привести к дизъюнктивной нормальной форме. Если встречаются другие булевские операции. то их можно заменить на соответствующие термы, построенные с помощью операций ˄, ˅ и ¬. Булевский терм t представлен в DNF, если (также после подготовительных преобразований по коммутативному закону) к t уже неприменимы последующие правила замены термов:
x1 ˄ (x2 ˅ x3) → (x1 ˄ x2) ˅ (x1 ˄ x3) ¬(x1 ˄ x2) → (¬x1 ˅ ¬x2)
¬(x¬¬x1→˅ xx2) → (¬x1 ˄ ¬x2)
x1 ˅ (x2 ˅ x3) → x1 ˅ x2 ˅ x3
x1 ˄ (x2 ˄ x3) → x1 ˄ x2 ˄ x3
x˅ x → x
x˄ x → x
x˄ ¬x → 0
0 ˄ x → 0
0 ˅ x → x.
При этом мы редуцируем по модулю коммутативности относительно ˄ и ˅. Это значит, что если необходимо, то сначала применяются законы коммутативности, прежде чем применяется одно из вышеуказанных правил.
Для приведения к DNF используются правила для исключения других логических операций, например:
(х => у) → ¬х ˅ у.
Чтобы с помощью заданных правил получить совершенную DNF, иногда п о- лезно дополнить заданный терм с помощью следующего правила:
t → (t ˄ у) ˅ (t ˄ ¬у).
При этом мы предполагаем, что идентификатор у не входит в t, но оказывается в другом частичном терме DNF.
Если мы стремимся к упрошенной DNF, то ее можно получить применением дополнительных правил, таких, как:
х ˅ (х ˄ у) → х,
3

(х ˄ у) ˅ (х ˄ ¬у) → х, x ˅ ¬x → 1 ,
х˅ 1 → 1,
х˄ 1 → х.
Чтобы получить наипростейшую (самую короткую) упрощенную DNF, часто бывает необходимо, исходя из совершенной DNF булевского терма, вначале продублировать в нем некоторые минтермы.
Переключательные схемы
Для реализации вычисления булевских функций могут использоваться переключательные схемы (П-схемы или просто схемы). Теперь эти булевские функции будем называть переключательными функциями, или, короче, П-функциями.
П-схемы соответствуют направленным ациклическим графам с входами и выходами (называемыми также заключениями). П-схема с n входами и m выходами есть направленный ациклический граф с n входными и m выходными ребрами, вершины которого помечены булевскими функциями (точнее, их именами).
Представление переключательных функций и схем
Переключательная функция f с n входами и m выходами есть отображе-
ние следующей функциональности: f: Вn → Вm.
Мы говорим о n-местной П-функции с m-местным результатом. Эти функции в схеме изображаются графически в виде "черного ящика” (англ. black box) с n входными и m выходными стрелками. Одно такое изображение приведено на рис. 2.1.
Рис. 2.1. п-местная компонента с т-местным результатом
Специальные изображения применяются для графического представления в схемах переключательных функций, которые соответствуют классическим логическим связям. На рис. 2.2 показан ряд примеров.
4

или
Рис. 2.2. Изображения переключательных функций
Приведенные на рис. 2.2 изображения соответствуют следующим П-функциям:
AND, OR: B2 → B, NOT: B → B, ANDn, ORn: Bn → B.
Вычисление значений функций определяется следующими равенствами: AND(a, b) = а ˄ b,
OR(a, b) = a ˅ b, NOT(a) = ¬a.
Приведенные изображения и их П-функции соответствуют элементам, объединяемым в П-схемы. Их называют также вентилями, а соответствующие им функции – вентильными функциями.
Пример (переключательная схема). На рис. 2.4 показана простая П-схема, ко-
торая реализует булевскую функцию f: В2 → В, определенную следующим об-
разом: f(a, b) = (a ˅ b) ˄ а.
Структура булевского терма (a ˅ b) ˄ а определяет П-схему.
Рис. 2.4. Пример простой переключательной схемы
Функциональные термы для представления переключательных схем описываются следующим синтаксисом:
<net> ::= <basic function> | |
(базисные функции) |
(<net> || <net>) | |
(параллельная композиция) |
(<net> • <net>) | |
(последовательная композиция) |
|<net>, <net>] |
(кортежирование) |
В качестве базовых функций в основном используются NOT, AND и OR. Таким образом, по этому синтаксису П-схема строится главным образом из указанных выше базисных функций с помощью двух типов композиции – параллельной и
5
последовательной. Третья форма связывания – кортежирование – введена только из соображений наглядности способа записи. С помощью этих видов композиций с заданными изображениями можно построить большое число схем (в форме ациклических направленных графов).
П-функции можно грубо разделить
•на арифметические функции для представления арифметических операций над числами в двоичном изображении;
•на логические функции для представления типичных операций логики над двоичными словами;
•на функции с управляющими линиями для передачи информации.
Рассмотрим функцию на примере полусумматора, который является важным элементом для арифметических переключателей.
Пример (полусумматор НА). Полусумматор – это П-функция с двумя
входами и двумя выходами: НА: В2 → В2.
Функция полусумматора задана табл. 2.3. При этом входы обозначены через а и b , а результаты – через s (сумма по модулю 2) и u (перенос).
а |
0 |
0 |
1 |
1 |
b |
0 |
1 |
0 |
1 |
f1(a, b) = s |
0 |
1 |
1 |
0 |
f2(a, b) = u |
0 |
0 |
0 |
1 |
Таблица 2.3. Таблица П-функции полусумматора
Выход s соответствует одноразрядному сложению (по модулю 2), а выход u представляет перенос. Мы получаем следующую упрощенную DNF для каждого из выходов:
s = (¬а ˄ b) ˅ (а ˄ ¬b), u = а ˄ b.
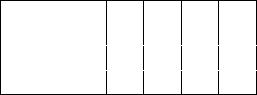
Логическая блок-схема устройства, реализующего полученную функцию, представлена на рис. . 2.13.1.
Рис. 2.13.1. Логическая блок-схема полусумматора
Преобразуем первое уравнение:
6
s = (а ˅ b) ˄ (¬а ˅ ¬b) = (а ˅ b) ˄ ¬(а ˅ b) = ¬(¬(а ˅ b) ˅ (а ˄ b)).
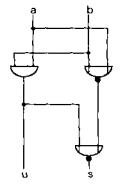
По этой формуле получается П-схема для пол усумматора, приведенная на рис. 2.13.2.
Рис. 2.13.2. Логическая блок-схема полусумматора
С помощью параллельного и последовательного связывания основных функций, а также перестановок и разветвлений линий связи можно создавать любые переключательные схемы и тем самым представлять любые переключательные функции. Заданные переключательные элементы и композиции схем соответствуют переключательным функциям и их композициям.
Конструирование переключательных схем
Кратко остановимся на способах систематического конструирования П-схем по таблице значении или по термовому представлению П-функции. Для этого поступают следующим образом. Исходя из таблицы значений, можно вывести для всех выходов булевские термы в DNF. Переведем булевские термы для значений выходов П-функции в функциональный терм, из которого путем применения законов алгебры получим П-функцию для схемы.
Применением правил преобразования для функционального терма в качестве следующих законов "алгебры П-функции” функциональные термы могут быть преобразованы в эквивалентные им термы. Благодаря этому функциональный терм, полученный из основных булевских функций и функций проекции применением кортежей и последовательной композиции (логическое представление), может быть переведен в функционально эквивалентный функциональный терм, построенный из основных булевских функций, функций идентичности, перестановки и разветвления с применением параллельной и последовательной композиций (физическое представление). Мы применяем законы следующего вида:
[f1 • g1, f2 • g2] = [f1, f2] • [g1, g2], [f • g1, f • g2] = f • [g1, g2]
При этом проверяется, что число выходных ребер у f1 (соответственно у f2) совпадает с числом выходных ребер у g1 (соответственно у g2). Аналогично проверяется для f и g1 (соответственно g2).
Арифметические схемы
Для реализации арифметических функций с помощью П-схем решающим является способ представления чисел, над которыми должны выполняться
7
арифметические операции, в виде двоичных слов. Сейчас мы рассмотрим натуральные и целые числа.
Рассмотрим две формы представления целых чисел в дополнительном коде, которые – наряду с уже описанным двоичным представлением для натуральных чисел – будем использовать при реализации арифметических функций с помощью переключательных схем. Мы рассмотрим сложение, вычитание, умножение, деление и сравнение при двоичном представлении чисел. При этом мы специфицируем по мере надобности соответствующие П-функции и опишем схемы для их реализации.
Первый пример для булевской функции, которая соответствует простой арифметической операции – это описанный выше полусумматор. Теперь рас-
смотрим полный сумматор, в котором имеются три входа и два выхода. Этот сумматор складывает 3 бита (три одноразрядных двоичные числа) и дает одно двухразрядное двоичное число. Таким образом, сумматор – это переключательная функция с функциональностью
VA: В3 → В2. |
|
|
|
|
|
|
|
|
|
|
Пусть (s, u) = VA |
(а, b, |
с). Переключательная |
функция VA описывается |
|||||||
табл. 2.4. |
|
|
|
|
|
|
|
|
|
|
|
а |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
|
|
b |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
|
|
с |
0 |
1 |
0 |
1 |
0 |
1 |
0 |
1 |
|
|
s |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
u |
0 |
0 |
0 |
1 |
0 |
1 |
1 |
1 |
|
Таблица 2.4. Таблица переключательной функции сумматора
Для выходов u и s получаем следующие равенства для термового представления сумматора (в упрощенной DNF):
u = (а ˄ b) ˅ (а ˄ с) ˅ (b ˄ с),
s = (¬а ˄ ¬b ˄ с) ˅ (¬а ˄ b ˄ ¬с) ˅ (а ˄ b ˄ ¬с) ˅ (а ˄ b ˄ с).
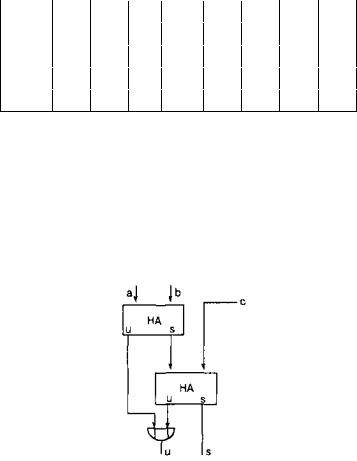
Сумматор соответствует приведенной на рис. 2.14 переключательной схеме, которая построена из двух полусумматоров.
Рис. 2.14. Сумматор
Из сумматоров можно индуктивно строить схемы сложения. Например, таким способом получаем следующую схему сложения для 4-разрядных двоичных чисел, показанную на рис. 2.15.
8
Рис. 2. IS. Четырехразрядная схема сложения
Умножение и деление неотрицательных двоичных чисел (числа в прямом коде) могут выполняться так же, как и при десятичной системе счисления. Умножение десятичных чисел сводится к последовательным умножениям одного числа на цифры другого числа и сложению этих частичных произведений со ступенчатым сдвигом каждого из них. При двоичных числах этот процесс упрощается, поскольку существуют только цифры 1 и 0, так что каждое ч а- стичное произведение равно либо нулю, либо множимому.
Деление десятичных чисел, как известно, выполняется через последовательность подходящего числа ступенчато сдвинутых вычитаний делителя из соответствующих частей делимого. При двоичных числах этот процесс упрощается, поскольку существуют только цифры 1 и 0, а потому каждый раз делитель вычитается не более одного раза.
Умножение двух n-разрядных двоичных чисел в общем случае дает 2n-разрядный результат. Это порождает трудности, если мы хотим работать с двоичными числами одинаковой длины. Эту трудность можно обойти, используя так называемые числа с фиксированной точкой. При этом мы получаем двоичное представление дробной части числа. В этом случае представимые числа лежат в интервале [0, 1 ]. Умножение чисел из этой области снова дает число из этого же интерва ла. То же самое имеет место для деления а / b, если а < b. Как при делении, так и при умножении получаются правильные дроби более чем с n разрядами. С помощью их округления снова получаются n- разрядные двоичные дроби. При этом возникают ошибки округления.
Логические или переключательные схемы для умножения и деления двоичных чисел строятся также из классических элементарных схем, полусумматоров, сумматоров и схем сдвига.
В современных компьютерах применяются системы интегральных элементов, у которых с целью большей унификации в качестве базовой логической схемы используется всего одна из схем: «НЕ — И» (NAND, штрих Шеффера), «НЕ — ИЛИ» (NOR, стрелка Пирса), а иногда и «НЕ – И – ИЛИ» (NORAND).
Переключательные схемы с управляющими линиями или функциональные схемы комбинационного типа
Это следующий уровень иерархии переключательных схем – переключа-
тельные (функциональные) схемы комбинационного типа. Переключательные
9
(функциональные) комбинационные схемы (комбинационные цепи) – это устройства, выходные величины которых зависят только от текущих значений входных величин. Они выполняют типовые для цифровых устройств микрооперации, т.е. реализуют низший иерархический уровень внутреннего языка цифрового устройства.
Для систем переработки информации наряду с арифметическими функциями необходим и класс переключательных функций для управления передачей данных. Эти функции также имеют отношение к переключательным схемам, которые реализуют управление связями. Для таких схем входы можно классифицировать на линии управления и линии данных. Значения на линиях управления устанавливают, какие из линий данных с какими выходами должны быть связаны и тем самым должны быть переключены на эти выходы. Чтобы установить, какие двоичные слова управляющих линий ведут к каким соединениям между линиями данных и выходов, используются двоичные коды натуральных чисел и соответствующие функции декодирования.
Рассмотрение функциональных узлов начнем с типовых комбинационных схем.
Дешифратор (Decoder, DC) осуществляет преобразование n-элементного параллельного кода в код «1 из m», у которого только в одной позиции находится единица, все остальные позиции – нулевые. Количество выходов так называемого полного дешифратора должно равняться числу всевозможных
n-разрядных кодовых комбинаций, т.е. m = 2n. Схемная реализация и условное обозначение двухвходового дешифратора представлены на рис.2.8.
Рис .2.8. Двухвходовый дешифратор
Информационные входы дешифратора принято обозначать их двоичными весами. EN (Enable) – вход разрешения работы дешифратора. На выходе дешифратора формируются логические функции в виде системы конъюнкций, которая в случае n информационных входов имеет вид:
|
_ _ |
_ |
_ |
F0 |
= x0 x1 |
….. xn-2 xn-1EN |
|
|
_ |
_ |
_ |
F1 |
= x0 x1 |
….. xn-2 xn-1EN |
|
|
_ |
_ |
_ |
F2 |
= x0 x1 ….. xn-2 xn-1EN |
||
………………………
10
