- •Министерство образования и науки российской федерации
- •Дифференциальные уравнения первого порядка
- •Уравнения с разделёнными и разделяющимися переменными
- •Однородные уравнения первого порядка
- •Линейные уравнения первого порядка
- •Уравнение в полных дифференциалах
- •Интегрирующий множитель
- •Дифференциальные уравнения высших порядков
- •Уравнения вида
- •Уравнения второго порядка, приводящиеся к уравнениям первого порядка
- •Линейные однородные уравнения. Определения и общие свойства
- •Линейные однородные уравнения второго порядка с постоянными коэффициентами
- •Линейные однородные уравнения го порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения второго порядка
- •Неоднородные линейные уравнения второго порядка с постоянными коэффициентами
- •Неоднородные линейные уравнения высших порядков
- •Системы обыкновенных дифференциальных уравнений
- •Системы линейных дифференциальных уравнений с постоянными коэффициентами
- •Р я д ы Числовые ряды Числовой ряд. Сумма ряда. Необходимый признак сходимости ряда
- •Достаточные признаки сходимости рядов с положительными членами
- •Знакопеременные ряды
- •Функциональные ряды
- •Ряды Тейлора и Маклорена
- •Ряды Фурье
- •Ряды Фурье для четных и нечетных функций
- •Ряд Фурье для функции с периодом
- •К о м б и н а т о р и к а
- •Общие правила комбинаторики
- •Соединения в комбинаторике
- •Размещения без повторений
- •Перестановки без повторений
- •Сочетания без повторений
- •Размещения с повторениями
- •11 12 13 14 15 16 17 19
- •Перестановки с повторениями
- •Т е о р и я в е р о я т н о с т е й Случайные события Основные понятия теории вероятностей
- •Основные теоремы теории вероятностей Теорема сложения вероятностей несовместных событий
- •Зависимые и независимые события. Условная вероятность
- •Теорема умножения вероятностей
- •Теорема сложения вероятностей совместных событий
- •Вероятность появления хотя бы одного события
- •. Формула полной вероятности
- •Формула Бейеса
- •Повторение испытаний
- •Формула Бернулли
- •Локальная теорема Лапласа
- •. Формула Пуассона
- •Интегральная теорема Лапласа
- •Случайные величины Случайная величина. Виды случайных величин
- •Закон распределения вероятностей дискретной случайной величины
- •Числовые характеристики дискретных случайных величин
- •Математическое ожидание дискретной случайной величины
- •Дисперсия дискретной случайной величины
- •Плотность распределения вероятностей непрерывной случайной величины
- •Числовые характеристики непрерывных случайных величин
- •Законы распределений
- •Равномерное распределение
- •Нормальное распределение
- •. Правило трёх сигм
- •Показательное распределение
- •Функция надёжности
- •Элементы математической статистики Основные сведения из математической статистики
- •Статистическое распределение выборки. Полигон и гистограмма
- •1 4 6
- •10 15 25
- •Статистические оценки параметров распределения
- •Оценка генеральной дисперсии по исправленной выборочной
- •Точность оценки, доверительная вероятность (надёжность). Доверительный интервал
- •Методы расчёта сводных характеристик выборки
- •Сведение первоначальных вариант к равноотстоящим
- •Оценка отклонения теоретического и эмпирического распределений от нормального. Асимметрия и эксцесс
- •Элементы теории корреляции
- •. (1)
- •(4) . (5) Корреляционная таблица
- •Отыскание параметров выборочного уравнения прямой линии регрессии по сгруппированным данным
- •Методика вычисления выборочного коэффициента корреляции
- •. Статистическая проверка статистических гипотез
- •Линейное программирование Задача линейного программирования
- •Построение математической модели
- •Графическое решение задачи линейного программирования
- •Симплексный метод решения задачи линейного программирования
- •Решение задачи 1 симплексным методом
- •Искусственное начальное решение. Метод больших штрафов.
- •Особые случаи применения симплекс-метода
- •1.7.2 Бесконечное множество решений
- •1.7.4 Неограниченные решения
- •1.7.5 Промежуточное вырожденное решение
- •Задача о назначениях
- •4 Изменение запаса ресурса продукта а 7
- •1 Изменение единицы стоимости продукта а 4
- •Заключение
Линейные однородные уравнения го порядка с постоянными коэффициентами
Рассмотрим
линейное однородное уравнение
 го
порядка:
го
порядка:
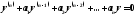
Для этого уравнения справедлива следующая теорема:
Если
функции
 являются линейно независимыми решениями
данного уравнения, то его общее решение
суть
являются линейно независимыми решениями
данного уравнения, то его общее решение
суть
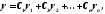
где
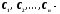 произвольные
постоянные.
произвольные
постоянные.
Если коэффициенты данного уравнения постоянны, то общее решение находится так же, как и в случае уравнения второго порядка:
Составляем характеристическое уравнение
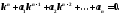
Находим корни характеристического уравнения
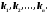
По характеру корней выписываем частные линейно независимые решения, руководствуясь тем, что:
каждому действительному однократному корню
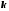 соответствует частное решение
соответствует частное решение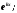
каждой паре комплексных сопряжённых однократных корней
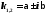 соответствуют два частных решения
соответствуют два частных решения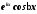 и
и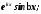
каждому действительному корню
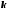 кратности
кратности соответствует
соответствует линейно независимых частных решений
линейно независимых частных решений
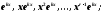
каждой паре комплексных сопряжённых корней
 кратности
кратности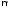 соответствуют
соответствуют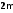 частных решений
частных решений
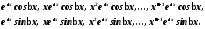
4.
Найдя
 линейно независимых частных решений
линейно независимых частных решений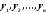 ,
строим общее решение данного линейного
уравнения
,
строим общее решение данного линейного
уравнения

Описанные выше шаги можно объединить в таблицу:


Характер корня
характеристического Частные решения уравнения
уравнения

1.
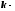 простой
простой
вещественный
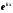
корень
2.
 вещественный
вещественный
корень
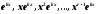
кратности

3.
 простые
простые
комплексные

сопряжённые корни
4.
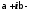 комплексные
комплексные
сопряжённые корни

кратности
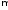
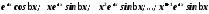
Неоднородные линейные уравнения второго порядка
Неоднородное линейное уравнение второго порядка имеет вид
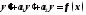
Общее
решение данного уравнения определяется
как сумма какого-нибудь частного решения
этого уравнения
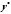 и общего решения
и общего решения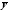 соответствующего однородного уравнения
соответствующего однородного уравнения
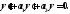

Так
как общее решение
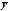 однородного уравнения
однородного уравнения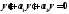 мы
уже умеем находить, то основная задача
при интегрировании неоднородного
уравнения
мы
уже умеем находить, то основная задача
при интегрировании неоднородного
уравнения
 состоит
в нахождении какого-нибудь его частного
решения
состоит
в нахождении какого-нибудь его частного
решения
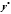 .
.
Укажем общий метод нахождения частных решений неоднородного уравнения, который называется методом вариации произвольных постоянных.
Общее
решение однородного уравнения имеет
вид
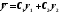 .
Будем искать частное решение неоднородного
уравнения
.
Будем искать частное решение неоднородного
уравнения в
такой же форме, предполагая
в
такой же форме, предполагая
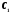 и
и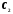 как некоторые пока неизвестные функции
от
как некоторые пока неизвестные функции
от ,
т.е.
,
т.е.
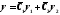 ,
(1)
,
(1)
где
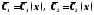 .
.
Продифференцируем
равенство (1):
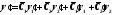 (2)
(2)
Подберём
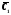 и
и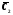 так, чтобы выполнялось равенство
так, чтобы выполнялось равенство ,
тогда
,
тогда
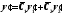 (3)
(3)
 (4)
(4)
Подставляя
(1), (3) и (4) в уравнение
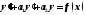 ,получим
,получим
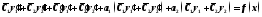 или
или
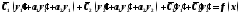
Т.к.
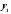 и
и -
решения однородного уравнения
-
решения однородного уравнения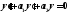 ,то
,то
 и
и
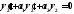 ,следовательно
,следовательно
 .
Таким образом, выражение (1) будет решением
неоднородного уравнения
.
Таким образом, выражение (1) будет решением
неоднородного уравнения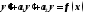 в
том случае, если
в
том случае, если
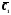 и
и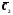 удовлетворяют системе уравнений:
удовлетворяют системе уравнений:
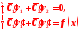 (5)
(5)
Так
как определителем этой системы является
определитель Вронского для линейно
независимых решений
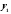 и
и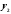 уравнения
уравнения ,то
он не равен нулю; следовательно, решая
систему, мы найдём
,то
он не равен нулю; следовательно, решая
систему, мы найдём
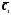 и
и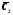 как определённые функции от
как определённые функции от :
: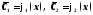 .
Интегрируя, получим
.
Интегрируя, получим ,
,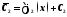 .
.
Подставив
значения
 и
и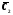 в выражение (1), найдём общее решение
неоднородного уравнения.
в выражение (1), найдём общее решение
неоднородного уравнения.
Решение
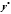 уравнения
уравнения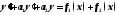 ,
где правая часть есть сумма двух функций
,
где правая часть есть сумма двух функций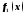 и
и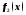 ,
можно представить в виде суммы
,
можно представить в виде суммы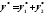 ,
где
,
где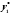 и
и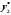 есть соответственно решения уравнений
есть соответственно решения уравнений