Министерство образования и науки Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования «Челябинский государственный университет»

КЛАССИЧЕСКОЕ УНИВЕРСИТЕТСКОЕ ОБРАЗОВАНИЕ

А. А. Бессонов

МЕХАНИКА

Конспект лекций

Челябинск Издательство Челябинского государственного университета

2013

СОДЕРЖАНИЕ

1. Векторы .. . . . . . . . .		.	.	.	.	.	.	. .			5
	1.1. Правила умножения векторных величин . . . . . . . . . . .										7
	1.2. Радиус-вектор . . . . .	.	.	.	.	.	.	. . . . .	.		9
2.	Кинематика точки.. . . .	.	.	.	.	.	.	. . . . .	. .		10
	2.1. Описание движения в координатной и векторной формах.. . .										10
	2.2. Перемещение. Скорость. . . . . . . . . . . .								. .	. . .	11
	2.3. Ускорение. . . . . . .	.	.	.	.	.	.	. . . .			13
3.	Кинематика твёрдого тела..	.	.	.	.	.	.	. . . . .	. .	. . .	16

3.1.Степени свободы твёрдого тела . . . . . . . . . . . . . . 16

3.2.Поступательное движение твёрдого тела . . . . . . . . . . 17

3.3.Вращательное движение . . . . . . . . . . . . . . . . . 18

3.4.	Угловая скорость. .	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.		19
3.5.	Угловое ускорение .	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	21

4.Динамика материальной точки . . . . . . . . . . . . . . . 22

4.1.Статическое и динамическое проявление сил . . . . . . . . 22

4.2. Измерение сил. . . . .	.	.	.	.	.	.	.	.	.	.	.	.					23
4.3. Первый закон Ньютона .	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	24
4.4. Второй закон Ньютона..	.	.	.	.	.	.	.	.	.	.	.	. .	.	.		.	26

4.5.Закон независимости действия сил . . . . . . . . . . . . . 28

4.6.Динамические уравнения движения материальной точки.. . . 28

4.7.Инерциальные и неинерциальные системы отсчёта. Преобразования Галилея.. . . . . . . . . . . . . . . . . 29

4.8. Третий закон Ньютона.. . . . . . . . . . . . . . . . .   31

5.Движение системы материальных точек . . . . . . . . . . . 33

5.1.Частично замкнутые системы.. . . . . . . . . . . . . . . 34

5.2. Центр масс.. . . . . .	.	.	.	.	.	.	.	.	.	. .		35
6. Движение тел переменной массы.. . . . . . . . . . . . . . .												37
6.1. Формула Циолковского .	.	.	.	. . . . . . . . . . . . .								39
6.2. Многоступенчатые ракеты . . . . . . . . . . . . . . . .												39
7. Энергия и работа . . . . .	.	.	.	.	.	.	.	.	.	.	. .	41
7.1. Кинетическая энергия .	.	.	.	.	.	.	.	.	.	.	. . . . . .	43
7.2. Связь между кинетическими энергиями в различных системах
отсчёта. Теорема Кёнига . . . . . . . . . . . . . . . . .												44
7.3. Потенциальная энергия .	.	.	.	.	. . . . . . . . . . . .							45
7.4. Связь между потенциальной энергией и силой . . . . . . . .												48
7.5. Силы и потенциальная энергия . . . . . . . . . . . . . .												50

7.6.Закон изменения механической энергии.. . . . . . . . . . . 51

7.7.Условие равновесия механической системы . . . . . . . . . 52

8. Удары . . . . . . . . . . . . . . . . .	55
8.1. Абсолютно неупругий удар. . . . . . . . . . . . . . . .	55
8.2. Абсолютно упругий удар . . . . . . . . . . . . . . . . .	59

3

9. Динамика твёрдого тела..	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	63
9.1. Уравнение моментов..	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	63

9.2.Закон сохранения момента импульса . . . . . . . . . . . . 65

9.3.Основное уравнение динамики вращательного движения.. . . 66

9.4.Вычисление моментов инерции . . . . . . . . . . . . . . 68

9.5.Теорема Гюйгенса — Штейнера.. . . . . . . . . . . . . . 69

9.6. Гироскоп. . . . . .	.	.	.	.	.	.	.	.	.	. .	71
9.7. Главные оси инерции .	.	.	.	.	.	.	.	.	.	. . . . . . .	73
9.8. Эллипсоид инерции твёрдого тела. Понятие о тензоре инерции.											.75
10. Колебательное движение тел.. . . . . . . . . . . . . . . .											80
10.1. Простейшие механические колебательные системы . . . . .											83
10.2. Энергия колебаний..	.	.	.	.	.	.	.	.	.	. . . . . . .	85

10.3. Затухающие колебания . . . . . . . . . . . . . . . . . 86 10.4. Векторная диаграмма.. . . . . . . . . . . . . . . . .   89 10.5. Вынужденные колебания. . . . . . . . . . . . . . . . . 90 10.6. Резонанс . . . . . . . . . . . . . . . . .             96

10.7.Добротность колебательной системы. . . . . . . . . . . . 99

10.8.Сложение колебаний, происходящих вдоль одной прямой . . 100

10.9.Сложение взаимно перпендикулярных колебаний . . . . . 105

10.10.Гармонический анализ сложных колебаний.. . . . . . . . 110

10.11.Колебания связанных систем. . . . . . . . . . . . . . 111

10.12.Представление гармонических колебаний в комплексной

форме .. . . . .	.	.	.	.	.	.	.	.	.	.	.	.					113
11. Волновые процессы .	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	.	115

11.1.Уравнение волны. Волновое уравнение.. . . . . . . . . . 118

11.2.Фазовая скорость упругих волн . . . . . . . . . . . . . 121

11.3.Интерференция волн. Стоячие волны . . . . . . . . . . . 122

11.4. Эффект Доплера . . . . . . . . . . . . . . . . .     125

12.Неинерциальные системы отсчёта. . . . . . . . . . . . . 128

12.1.Силы инерции при поступательном движении (силы инерции

Даламбера).. . . . . . . . . . . . . . . . .	128
12.2. Силы инерции, действующие на покоящееся тело
во вращающейся системе отсчёта (силы инерции Эйлера) . .	129

12.3.Силы инерции, действующие на движущееся тело во вращающейся системе отсчёта (силы инерции Кориолиса). 130

12.4.Силы инерции во вращающейся системе координат.. . . . . 133

12.5.Законы сохранения в неинерциальных системах. . . . . . 134

12.6.О реальности существования сил инерции. . . . . . . . . 134

13.Понятие о механике теории относительности. . . . . . . . 135

13.1.Следствия из преобразований Лоренца.. . . . . . . . . . 136

Список рекомендуемой литературы . . . . . . . . . . . . . . 143

4

Рис. 2. К понятию перемещения

Рис. 1. К понятию вектора

Вернуться 1. ВЕКТОРЫ Дальше

Многие физические величины характеризуются одним числом. К ним, например, относятся масса, температура и т. д. Такие величины называются скалярами. Для характеристики многих других физическихвеличиннеобходимозадатьнесколькочисел.Например, скорость определяется нетолько числовым значением, но инаправлеφ φ - нием. Направление впространстве полностью задаётся углами иθ (рис. 1). Поэтому скорость характеризуется тремя числами ( , θ, v).

Вектор— упорядоченная совокупность трёх чисел (представляющих собой физические величины),

зависящих от системы координат

и изменяющихся при повороте си-

стемы отсчёта так же, как изменя-

ются координаты точки.

Геометрический образ векто-

ра — это направленный отрезок

прямой, определённым образом ориентированный в пространстве.

Перемещение точки в пространстве за любой промежуток времени можно изобразить вектором. Например, в момент t1 она

была в точке А, а в момент t2 — в точке В (рис. 2). Тогда перемещение за время t2 – t1 изобразится вектором AB . Отметим, что век-

тор перемещения только в случае

одностороннего прямолинейного

движения будет совпадать с тра-

екторией движущейся точки. При

криволинейном движении траекто-

рией точки является кривая, проходящая через точкиА иВ(см. рис. 2).

Векторы считаются одинаковыми, когда они представляются равными параллельными отрезками и направлены в одну сторону.

Длина отрезка, измеренная вопределённом масштабе, равна абсолютной величине, или модулю вектора.

Например, AB — вектор, АВ или | AB | — модуль вектора.

5

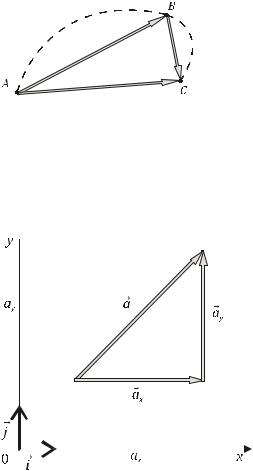
Если точка переместилась изВ вС (рис.3), то эта последовательность перемещений эквивалентна одному перемещению из А в С,

	что записывается ввиде векторного
	равенства AB + BC = AC. Эта фор-
	мула выражает правило сложения
	векторов.
	По этому же правилу про-
	исходит и вычитание векторов
Рис. 3. Сложение векторов	BC = AC − AB .
	Обычно при действиях с век-

торными величинами удобно представлять векторы их проекциями по заданным определённым направлениям. Поясним это вначале для векторов, лежащих в плоскости. Выберем на плоскости прямоугольную систему координат x, y (рис. 4), тогда любой вектор a можно представить как сумму a = ax + ay , где ax — вектор, направленный вдоль оси x и называемый проекцией (составляющей) или компонентой вектора

a

по оси x; аналогично

ay

— компонента векто-

ра a по оси y.

ay

Очевидно, что ax и

однозначно опреде-

ляют величину инаправ-

ление вектора a . Обозна-

чим через i единичный

вектор вдоль оси х, а че-

рез j —единичныйвек-

тор вдоль оси y.

Единичным

векто-

ром по определению на-

Рис. 4. Проекции вектора

зывают вектор,

модуль

которого равен единице.

Единичный вектор указывает только направление в пространстве. Тогда составляющие вектора можно записать так: ax = axi , ay = ay j, где ax и ay — уже не векторы, а обычные числа — скаляры. Числа ax и ay называются проекциями a на определённые направления,указанныевекторами i и j, илипростопроекциями

вектора на данные координатные оси x иy (см. рис. 4). Следователь-

но, a = axi + ay j.

6

Модуль (или длина) вектора a, лежащего в плоскости, равен a = | a | = ax2 + ay2 .

Если вектор a расположен в пространстве (а не на плоскости), то его можно относить к прямоугольной системе координат x, y, z.

Единичныйвекторвдольоси z, перпендикулярный квекторам i и j, обычно обозначают k. Тогда, рассуждая аналогичным образом, можем записать вектор a через компоненты так:

a = a	x	+ a	y	+ a	или a = a	x	i + a	y	j + a	k.
				k					z
Модуль вектора		представится выражением

a= | a | = ax2 + ay2 + az2 .

1.1.Правила умножения векторных величин

1.Умножение вектора a начисло β записывается как βa иозначает изменение модуля вектора в β раз с сохранением его направления(еслиβ>0)илиизменениемнаправлениянаобратное(еслиβ<0).

Различают два вида умножения векторов: скалярное и вектор-

ное; в первом случае произведение векторов — скаляр, во втором — вектор.

2. Скалярное произведение двух векторов a и b по определению равно произведению модулей этих векторов на косинус угла α между ними:

(a,b)= ab cos(a ^ b) = ab cos α .

Скалярное произведение двух взаимно перпендикулярных векторов равно 0. Очевидно, (a,b)= (b, a).

Скалярное произведение обладает свойством распределительности:

(a,(b + c))= (a,b)+(a, c).

Можно показать, что (a, αb)= (αa,b)= α(a,b).

Выразим скалярное произведение двух векторов через их про-

екции:	(a,b)= ((ax i + ay j + az k )(bx i +by j +bz k ))=
	= axbx (i,i)+ aybx (j,i)+ azbx (k,i)+

7

+axby (i, j)+ ayby (j, j)+ azby (k, j)+

+axbz (i, k )+ aybz (j, k )+ azbz (k, k )=

= axbx + ayby + azbz .

Мы использовали, что

(i,i)= (j, j)= (k, k )=1,

(i, j)= (i, k )= (j, k )= 0.

Скалярное произведение двух векторов равно сумме произведений соответствующих проекций на оси координат:

(a,b)= axbx + ayby + azbz .

3.Векторноепроизведениедвухвекторов a и b поопределению равно вектору c, нормальному к плоскости векторов a и b , модуль

которого равен absin α, где α— угол между векторами сомножителями (рис. 5).

4. По определению

		a,b = c
	и | c |=| a,b |=| a || b | sin (a ^ b)=| a || b | sin α .
	Правилобуравчика(винта)длявектор-
	ногопроизведения. Если нарисовать векторы
	так, чтобы их начала совпадали и вращать
	первый вектор-сомножитель кратчайшим
	образом ко второму вектору-сомножителю,
Рис. 5. К понятию векторно-	тобуравчик(винт),вращающийсятакимже
	образом, будет завинчиваться в направле-
го произведения	нии вектора-произведения.

Можно также сказать, что модуль векторного произведения равен площади параллелограмма, построенного на перемножаемых векторах.

Легко проверить следующие свойства векторного произведения:

a,b = − b, a ;

a,(b + c) = a,b + a, c ;a, αb = αa,b = α a,b .

8

Здесь учтено, что

Представим векторное произведение двух векторов через их проекции на координатные оси:

c = a,b = (ax i + ay j + az k ),(bx i +by j +bz k ) = (aybz − azby )i +(azbx − axbz ) j +(axby − aybx )k = cx i + cy j + cz k.

= k,

= −

=i,

i,

j

= − j,i

j, k

k, j

=

= 0.

k,i

= − i, k

j,

i,i

= j, j

= k

, k

Отсюда следует, что векторное произведение a,b можно записать в виде символического определителя

a	,b			i		j		k
			=	a	x	a	y	a	z	.
				bx		by		bz

Складывая векторы a и b, получаем

c= a +b = i (ax +bx )+ j (ay +by )+ k (az +bz )=

=cx i + cy j + cz k.

Следовательно, проекции суммы двух векторов равны сумме соответствующих проекций слагаемых cx = ax +bx , cy = ay +by , cz = az +bz .

1.2. Радиус-вектор

Положение точек пространства удобно характеризовать их ра- диус-векторами. Радиусом-вектором точки М называется вектор

r, начало­	которого совпадает с точкой начала системы координат,
		а конец — с рассматриваемой точкой
		(рис. 6).
		Если положение точки задаётся ра-
Рис. 6. Радиус-вектор		диус-вектором, то нет необходимости
		использовать какую-либо систему ко-

ординат. С помощью радиус-вектора положение точек описывается в бескоординатной форме.

9