математика

Пусть = max16i6n li наибольшая из длин дуг деления. Если при ! 0 (тогда n ! 1) существует конечный предел инте-

гральных сумм (12), то его называют криволинейным интегралом от функции f(x; y) по кривой AB (èëè I ðîäà) и обозначают

Z	f(x; y) dl = Z	n
		n!1 ( !0) i=1 f (^xi; y^i) li:
AB	L	X	(13)
	f(x; y) dl =	lim

Условие существования криволинейного интеграла I рода (существование предела интегральной суммы (12) при n ! 1 ( ! 0))

представляет следующая теорема.

Теорема 3 Если функция f(x; y) непрерывна в каждой точке гладкой кривой (в каждой точке (x; y) 2 L существует касательная к

данной кривой и положение ее непрерывно меняется при перемещении точки по кривой), то криволинейный интеграл I рода существует и его величина не зависит ни от способа разбиения кривой на части, ни от выбора точек в них.

Процесс построения криволинейного интеграла I рода (по кривой) похож на процедуру определения интеграла функции одной переменной на отрезке. Аналогичны и свойства интегралов и их доказательства.

Основные свойства криволинейного интеграла I рода (по кривой)

Приведем основные свойства криволинейного интеграла по кривой (I рода).

RR

1.f(x; y) dl = f(x; y) dl, т. е. криволинейный интеграл I

AB BA

рода не зависит от направления пути интегрирования.

RR

2.c f(x; y) dl = c f(x; y) dl; c const:

LL

R	R	R
3.	(f1(x; y) f2(x; y)) dl =	f1(x; y) dl f2(x; y) dl:
L	L	L

31

R

R

R

4.

f(x; y) dl =

f(x; y) dl +

f(x; y) dl, если путь интегриро-

L

L1

L2

L = L1 [ L2

вания

L

разбит на части

L1

è

L2

такие, что

è

L1

è L2 имеют единственную общую точку.

5.

Если для точек кривой L выполнено неравенство f(x; y)

6

RR

g(x; y), òî f(x; y) dl 6 g(x; y) dl.

LL

6.Если функция f(x; y) непрерывна на кривой AB, то на этой кривой найдется точка (xc; yc) такая, что

Z

f(x; y) dl = f(xc; yc) l

(теорема о среднем):

AB

Вычисление криволинейного интеграла I рода

Вычисление криволинейного интеграла I рода может быть сведено к вычислению определенного интграла. Приведем без доказательства правила вычисления криволинейного интеграла I рода в случаях, если кривая L задана явным, параметрическим и поляр-

ным образом.

а) Явное представление кривой интегрирования.

Если кривая AB задана уравнением y = '(x), x 2 [a; b], где '(x) непрерывно дифференцируемая функция, то

b

ZZ

q

f(x; y) dl = f (x; '(x)) 1 + (yx0 )2dx: (14)

AB a

Подынтегральное выражение в правой части формулы (14) ïîëó-

ференциал дуги кривой.

y = '(x)

dl = q1 + (yx0 )

dx

чается заменой в левой части

è

2

äèô-

Задача 1. Вычислить

R

xy2 dl, где L отрезок прямой между

точками O(0; 0) и A(4; 3).

L

Решение: Уравнение прямой OA есть y = 3x=4,

0 6 x 6 4. Ñî-

гласно формуле (14) имеем

4

4

s1 + 4

dx =

64

x3 dx = 45:

Z

xy2 dl = x 4 x

2

Z

3

2

3

45

Z

L

0

0

32

б) Параметрическое представление кривой интегрирования. Если кривая AB задана параметрически уравнениями x = x(t),

y = y(t), t 2 [ ; ], где x(t) и y(t) непрерывно дифференцируемые функции параметра t, причем точке A соответствует t = , точке B значение t = , то

Z	Z	f (x(t); y(t)) q					dt:
AB f(x; y) dl =						(xt0)2 + (yt0)2		(15)
Задача 2. Вычислить		R	p2y dl, где L первая арка циклоиды

L

(

x = t sin t;

y = 1 cos t:

Решение:

Ðèñ. 22.

По формуле (15) получим

2

ZZ

qq

p

2y

dl =

2 (1 cos t) (1 cos t)2 + sin2 t dt =

L0

2

Z

= 2 (1 cos t) dt = 2 (t sin t)j20 = 4 :

0

в) Полярное представление кривой интегрирования.

Если плоская кривая L задана уравнением r = r('), 6 ' 6

q

в полярных координатах, то dl = r2 + r'0 2d'. Значит

ZZ

q

f(x; y) dl = f (r cos '; r sin ') r2 + r'0 2d': (16)

33

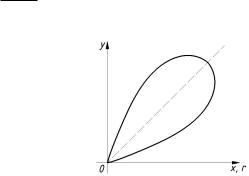
r = psin 2',	R	I координатном углу.
Задача 3. Вычислить		(x + y) dl, где L лепесток лемнискаты

L

расположенной в

Решение:

Ðèñ. 23.

Воспользуемся формулой (16). Так как

dl = s	sin 2' + sin 2'		d' = psin 2' =				r ;
		cos2 2'			d'		d'

то, заметив, что 0 6 ' 6 =2, получаем

	=2		r	=2
Z (x + y) dl = Z		(r cos ' + r sin ')		= Z	(cos ' + sin ') d' = 2:
			d'
L	0			0

Криволинейный интеграл II рода. Основные понятия

Криволинейный интеграл II рода определяется почти так же, как и интеграл I рода.

Пусть в плоскости Oxy задана непрерывная кривая AB (или L) и функция P (x; y), определенная в каждой точке кривой. Разобьем

кривую AB точками M0 = A; M1; : : : ; Mn = B в направлении от точки A к точке B на n äóã M\i 1Mi с длинами li (i = 1; : : : ; n).

На каждой элементарной дуге M\i 1Mi возьмем точку (^xi; y^i) è
составим сумму	n
	Xi
	P (^xi; y^i) xi;	(17)
	=1

ãäå xi = xi xi 1 проекция дуги M\i 1Mi íà îñü Ox.

34

Ðèñ. 24.

Сумму (17) называют интегральной суммой для функции P (x; y)

по переменной x. Таких сумм можно составить бесчисленное мно-

жество.

Åñëè ïðè = max16i6n li ! 0 интегральная сумма (17) имеет конечный предел, не зависящий ни от способа разбиения кривой AB, ни от выбора точек (^xi; y^i), то его называют криволинейным интегралом по координате x (или II рода) от функции P (x; y) ïî

R		R
кривой AB и обозначают	P (x; y) dx èëè P (x; y) dx. Èòàê,
AB		L
Z	n
	n!1 ( !0) i=1	i i	i
AB	X	P (^x ; y^ ) x :
P (x; y) dx =	lim
Криволинейный интеграл от функции Q(x; y) по координате y
вводится аналогично:
Z	n
	n!1 ( !0) i=1	Q (^xi; y^i) yi;
AB	X
Q(x; y) dy =	lim

ãäå yi = yi yi 1 проекция дуги M\i 1Mi íà îñü Oy.

Криволинейный интеграл II рода общего вида (по координатам)

R

P (x; y) dx + Q(x; y) dy определяется равенством

AB	P (x; y) dx + Q(x; y) dy = Z	P (x; y) dx + Z
Z			Q(x; y) dy:
AB	AB	AB

Теорема 4 Если кривая AB гладкая, а функции P (x; y) и Q(x; y) непрерывные на кривой AB, то криволинейный интеграл по координатам (II рода) существует.

35

Некоторые свойства криволинейного интеграла II рода

Перечислим лишь особые свойства криволинейного интеграла по координатам.

1.При изменениии направления пути интегрирования криволинейный интеграл II рода изменяет свой знак на противопо-

ложный, т. е.	Z	= Z
			:
	AB	BA

Это происходит потому, что проекции дуги M\i 1Mi íà îñè Ox

и Oy меняют знаки с изменением направления.

2.Если кривая AB есть прямая, параллельная оси Oy, то

Z

P (x; y) dx = 0 (âñå xi = 0);

L

аналогично, если кривая AB является прямой, параллельной оси Ox, то

Z

Q(x; y) dy = 0 (âñå yi = 0):

L

3. Криволинейный интеграл по замкнутой кривой (обозначает-

H

ся ) не зависит от выбора начальной точки (зависит только от направления обхода кривой).

Вычисление криволинейного интеграла II рода

Вычисление криволинейного интеграла II рода, как и I рода, может быть сведено к вычислению определенного интеграла.

а) Явное задание кривой интегрирования.

Если кривая AB задана уравнением y = '(x), x 2 [a; b], где функция '(x) и ее производная '0(x) непрерывны на отрезке [a; b],

36

òî dy = '0(x)dx и тогда

Z	P (x; '(x)) dx + Q(x; '(x)) dy =
AB
	b
	= Z hP x; '(x) +Q(x; '(x))'0(x)idx: (18)
	a
Задача 4. Вычислить I =		(x y)2 dx + (x + y)2 dy, ãäå L
ломаная OAB, O(0; 0), A(2; 0); BR		(4; 2).
	L

Решение:

Ðèñ. 25.

R

R

RAB y = x

отрезка OA есть y = 0, 0

x

2,

2

Òàê êàê L = OAB = OA + AB, òî I =

=

+

. Уравнение

6

6

L

OA AB

уравнение отрезка

:

,

x 2 [2; 4]. Согласно формуле (18) имеем

2

4

(x (x 2))2

I = Z

(x 0)2 + 0 dx + Z

+ (x + x 2)2 dx =

0

2

h

i

x3

2

4

+

x 2)3

4

=

8

8) +

1

136

3

0

+ 4x 2

(2 2 3

2

3 + (16

6(216 8) = 3

:

б) Параметрическое задание кривой интегрирования.

Пусть кривая AB задана параметрически уравнениями x = x(t),

и y = y(t), где функции x(t) и y(t) непрерывны вместе со своими производными x0(t) è y0(t) на отрезке [ ; ], причем начальной

точке A кривой соответствует значение параметра t = , а конеч-

ной точке B значение t = . И пусть функция P (x; y) непрерывна на кривой AB. Тогда P (x; y) = P x(t); y(t) , dx = x0t dt, à

37

P dx + Q dy =

Q(x; y) = Q x(t); y(t) , dy = yt0 dt для Q(x; y) непрерывной на кривой AB. Значит

Z	b
	P (x; y) dx + Q(x; y) dy = Z	P	x(t); y(t) xt0	+ Q x(t); y(t) yt0		dt:
AB	a h					i

Задача 5. Вычислить I = R (xy 1) dx+x2y dy от точки A(1; 0)

AB

до точки B(0; 2) по дуге эллипса x = cos t, y = 2 sin t.

Решение: Точке A соответствует t = 0, точке B t = =2; dx =sin t dt, dy = 2 cos t dt. Таким образом,

=2

Z

I = (cos t 2 sin t 1)( sin t dt) + cos2 t 2 sin t 2 cos t dt =

0

=2

Z

=4 cos3 t sin t + sin t 2 sin2 t cos t dt =

	0
	=2		=2		=2
= 4	Z0	cos3 t d(cos t) + Z0		sin t dt 2	Z0	sin2 t d(sin t) =
		=					=2	=	3:
			cos4 t cos t 3 sin3 t 0
						2			4

Замечание. Криволинейные интегралы I и II рода (по кри-

R

вой и по координатам) связаны соотношением

AB

R

P cos +Q cos dl, где и углы, образованные касательной

AB

к кривой AB в точке M(x; y) с осями Ox и Oy соответственно.

Задачи.

áîëû

2

, отсеченная кривой

2

R .

1. Вычислить криволинейный интеграл

y dl, ãäå L äóãà ïàðà-

L

y

= 2x

x = 2y

R

dl

прямой

, заключенный

2. Вычислить криволинейный интеграл L x y , ãäå L отрезок

y = x=2 2

между точками

A(0; 2)

è

B(4; 0).

38

3.

Вычислить криволинейный интеграл

dl

L отрезок

L

x+y , ãäå

прямой AB от A(2; 4) до B(1; 3).

R

4.

Вычислить криволинейный интеграл

x dl, ãäå L äóãà ïà-

L

y

2

раболы

, заключенная между

точками

è

.

y

= 2x

R

(2; 2)

(8; 4)

5.

Вычислить криволинейный интеграл

y2 dl, ãäå L äóãà öèê-

лоиды

,

ïðè

L

.

x = t sin t

y = 1 cos t

R

[0; 2 ]

t 2

6.

Вычислить криволинейный интеграл

x2 + y2 dl, ãäå L äó-

L

га полуокружности x = cos t, y = sin tR.

7.

Вычислить криволинейный интеграл

dl, где L астроида

L

x = cos3 t,

y = sin3 t.

R

Вычислить,

L x p

8.

x.2

y2 dl, где L половина лемнискаты r =

p

R

cos 2' '

2 [0; ]

9.

Вычислить криволинейный интеграл

x2 + y2 dl, ãäå L

окружность r = cos '.

L

R p

10.

Вычислить интеграл

y dx x dy, где L эллипс x = a cos t,

L

y = b sin t,

0 6 t 6 2 .R

11.

Вычислить

x2 dx xy dy, åñëè

AB

,

, лежащая в

à) AB

дуга окружности

x = cos t

y = sin t

R

I четверти и пробегаемая против часовой стрелки.

б) AB отрезок прямой от A(1; 0) до B(0; 1).

(0;1)

(0R;0)

2

вдоль линий:

12.

Вычислить

2xy2dx + x dy

3

; ã) y

2

= x.

a) y = x; á) y = x ; â) y = x

13.

Вычислить

x2 + y2

dy, где L контур четырехугольника с

L

вершинами RA(0; 0), B(2; 0), C(4; 4), D(0; 4).

39

	координат)	R
14.	Вычислить	(2 y) dx (1 y) dy, где L первая (от начала
		L				x = t sin t	,	y = 1 cos t	.
		арка циклоиды
15.	Вычислить		2 dx	x2 dy
		y	2		2 , ãäå L полуокружность x = 2 cos t,
	y = 2 sin t îòRt1		= 0 äî t2 = .
			x +y

L

Занятие 5

Формула Грина

Связь между двойным интегралом по области D и криволинейным интегралом по границе L этой области устанавливает формула

Грина, которая широко применяется в математическом анализе. Пусть на плоскости Oxy задана область D, ограниченная кри-

вой, пересекающейся с прямыми, параллельными координатным осям, не более чем в двух точках, т. е. область D правильная.

Теорема 5 Если функции P (x; y) è Q(x; y) непрерывны вместе со

своими частными производными @P	@Q	D, то имеет
@y	è @x в области
место формула

ZZ	@x	@y	dxdy = IL P dx + Q dy;	(19)
	@Q	@P

D

ãäå L граница области D и интегрирование вдоль кривой L произ-

водится в положительном направлении (т. е. при движении вдоль кривой область D остается слева).

Формула (19) называется формулой Грина.

Замечание. Формула (19) справедлива и для произвольной области, которую можно разбить на конечное число правильных областей.

Задача 1. С помощью формулы Грина вычислить

I = I		x2 + y2 dx + y		xy + ln x +		x2	+ y2	dy;
L	p				p

40