Лекция дискрет 08

Доказали замкнутость множества обобщённых пифагоровых троек P относительно бинарной операции , определив тем самым

алгебру [ P; ] типа (2)

Пример выполнения операции

(a1, b1, c1) = (3, 4, 5)			a3 = a1a2 – b1b2 = 15 – 48 = - 33
(a2, b2, c2) = (5, 12, 13)			b3 = a1b2 + a2b1 = 36 + 20 = 56
			c3 = c1c2 = 5 13 = 65
a	2 + b 2 = 1089 + 3136 = 4225 = 652 = c 2
3	3	3

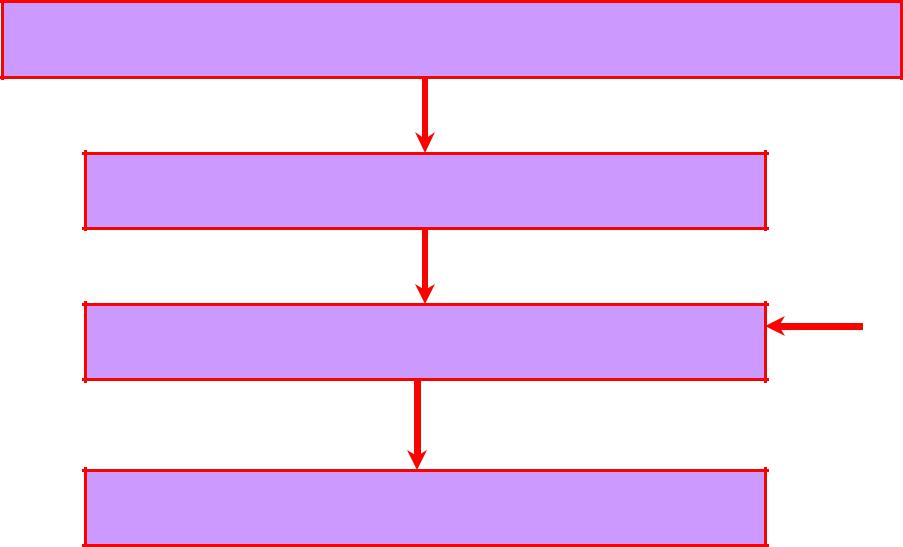
Итак, имеем мультипликативную алгебру типа (2) [ P; ]

Полугруппа – алгебра с одной ассоциативной операцией

+ коммутативность

Абелева (коммутативная) полугруппа

+ нейтральный элемент

Моноид

+ обратный элемент

Группа

+ нейтральный элемент

Исследование алгебры [ P; ]

Ассоциативность операции

(a , b , c ) = ((a1, b1, c1) (a2, b2, c2)) (a3, b3, c3) =

= (a1a2 – b1b2, a1b2 + b1a2, c1c2 ) (a3, b3, c3)

a = (a1a2–b1b2)a3–(a1b2+b1a2)b3 = a1a2a3–b1b2a3–a1b2b3-b1a2b3

b = (a1a2–b1b2)b3+(a1b2+b1a2)a3 = a1a2b3–b1b2b3–a1b2a3-b1a2a3 c = c1c2c3

(a , b , c ) = (a1, b1, c1) ((a2, b2, c2) (a3, b3, c3)) =

= (a1, b1, c1) (a2a3 – b2b3, a2b3 + b2a3, c2c3 )

a = a1(a2a3–b2b3)–b1(a2b3+b2a3) = a1a2a3–a1b2b3–b1a2b3-b1b2a3 b = b1(a2a3–b2b3)+a1(a2b3+b2a3) = a1a2b3–b1b2b3–a1b2a3-b1a2a3

=a

=b

c = c3c1c2 = c

Итак, полугруппа [ P; ]

Итак, имеем мультипликативную алгебру типа (2) [ P; ]

Полугруппа – алгебра с одной ассоциативной операцией

+ коммутативность

Абелева (коммутативная) полугруппа

+ нейтральный элемент

Моноид

+ обратный элемент

Группа

+ нейтральный элемент

Коммутативность операции

(a1, b1, c1) (a2, b2, c2) = (a1a2 – b1b2, a1b2 + b1a2, c1c2 ) = (a2a1 – b2b1, a2b1 + b2a1, c2c1 ) = (a2, b2, c2) (a1, b1, c1)

Итак, абелева полугруппа [ P; ]

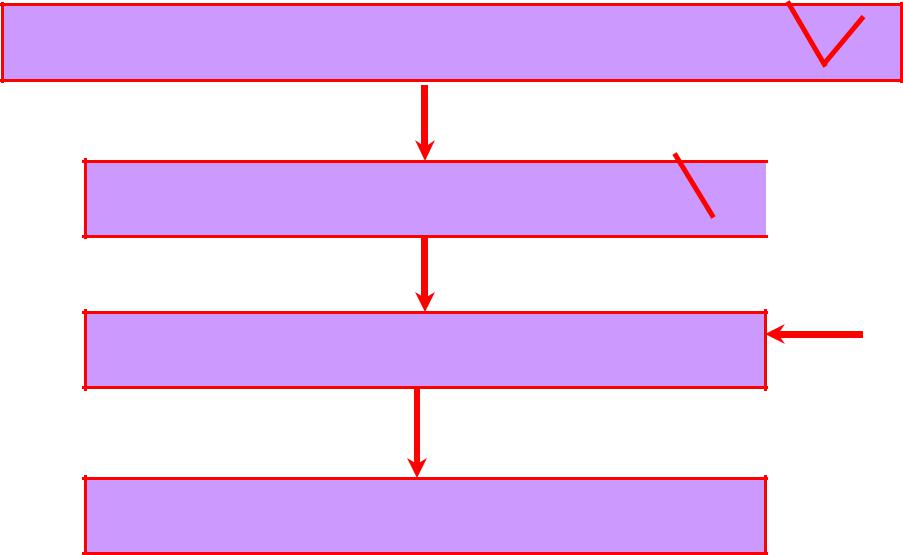
Итак, имеем мультипликативную алгебру типа (2) [ P; ]

Полугруппа – алгебра с одной ассоциативной операцией

+ коммутативность

Абелева (коммутативная) полугруппа

+ нейтральный элемент

Моноид

+ обратный элемент

Группа

+ нейтральный элемент

Нейтральный элемент относительно операции

e = (1, 0, 1):

(a, b, c) (1, 0, 1) = (a 1 – b 0, a 0 + b 1, c 1) = (a, b, c)

(1, 0, 1) (a, b, c) = (1 a – 0 b, 1 b + 0 a, 1 c) = (a, b, c)

Итак, моноид [ P; ]

Итак, имеем мультипликативную алгебру типа (2) [ P; ]

Полугруппа – алгебра с одной ассоциативной операцией

+ коммутативность

Абелева (коммутативная) полугруппа

+ нейтральный элемент

Моноид

+ обратный элемент

Группа

+ нейтральный элемент

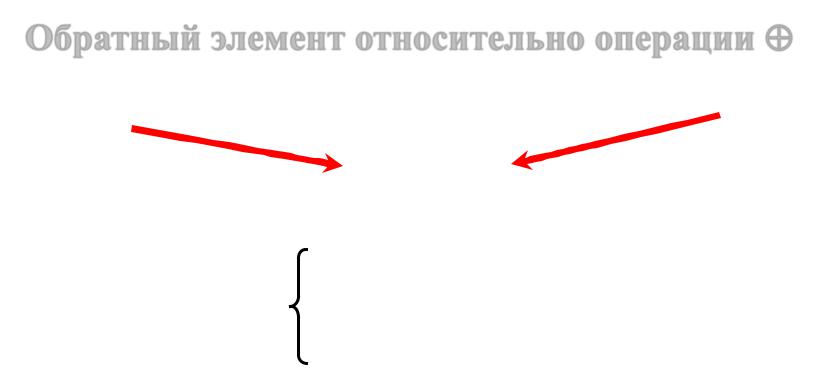
Обратный элемент относительно операции

(a, b, c) (x, y, z) = (1, 0, 1)		(x, y, z) (a, b, c) = (1, 0, 1)

(ax – by, ay + bx, cz) = (1, 0, 1)

					ax – by = 1
					bx + ay = 0
					cz = 1
	a			-		b			1
(x, y, z) = (			,				2 ,			)
	a2 + b2					a2 + b			c

[ a, b, c – целые числа, поэтому полученные для x, y, z выражения – рациональные числа ]

Итак, абелева группа [ P; ]

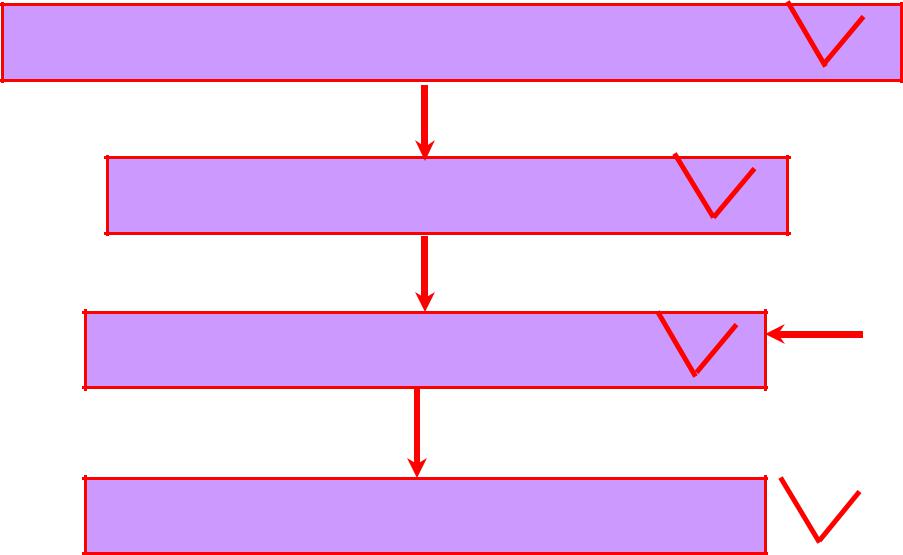
Итак, имеем мультипликативную алгебру типа (2) [ P; ]

Полугруппа – алгебра с одной ассоциативной операцией

+ коммутативность

Абелева (коммутативная) полугруппа

+ нейтральный элемент

Моноид

+ обратный элемент

Группа

+ нейтральный элемент