Лекция дискрет 08

b) Модель скрещивания организмов

При выведении породы крупного рогатого скота рассматривают цвет, чёрный или бурый, и признаки одноцветности или пятнистости. Известно, что чёрный цвет доминантен, а бурый рецессивен, и что одноцветность доминирует над пятнистостью.

Различают четыре типа скота: a – «чёрный одноцветный»

b – «чёрный пятнистый» c – «бурый одноцветный» d – «бурый пятнистый»

- операция скрещивания

Например, с учётом отношения доминирования, при скрещивании чёрной пятнистой особи с бурой одноцветной особью следует ожидать чёрное одноцветное потомство. Это можно записать в виде b c = a. Вся операция скрещивания описывается таблицей Кэли

	a	b	c	d
a	a	a	a	a
b	a	b	a	b
c	a	a	c	c
d	a	b	c	d

Из таблицы: - ассоциативна и коммутативна, d – нейтральный элемент относительно операции Требование наличия обратного элемента

– не выполняется

Итак, моноид [ { a, b, c, d }; ]

2) Алгебры преобразований

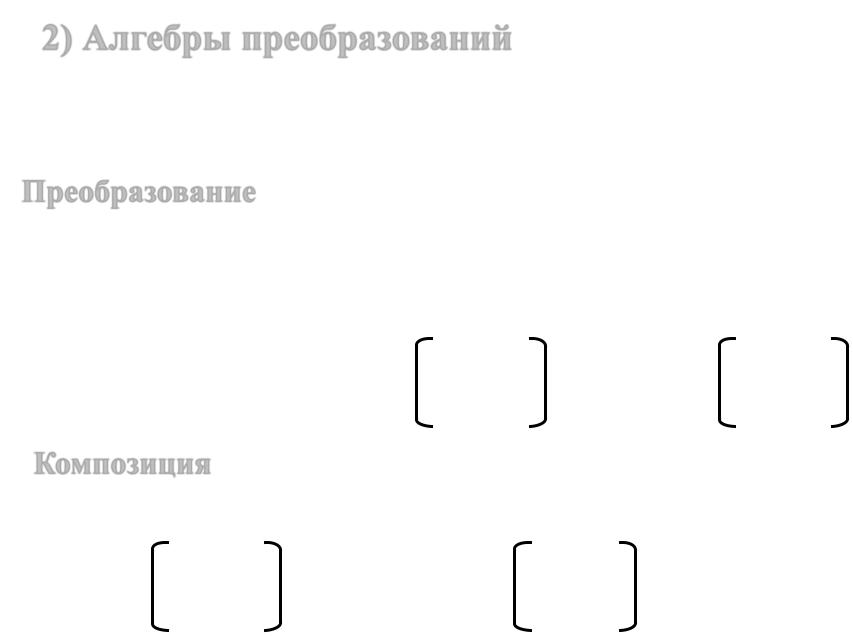
Преобразование множества М – всюду определённое функциональное соответствие f: M Μ (§ 1.2)

Преобразование конечного множества M = { m1, m2, … , mn } - постановка в соответствие каждому элементу mi M элемента mj M того же множества (не требуя при этом сюръективность и инъективность), например:

M = { 1, 2, 3 }					1	2	3			1	2	3
				α =					β =
					1	2	2			3	3	2
Композиция			преобразований – последовательное
выполнение двух преобразований:
αΔβ =	1	2	3		βΔα =		1	2	3
	3	3	3				2	2	2

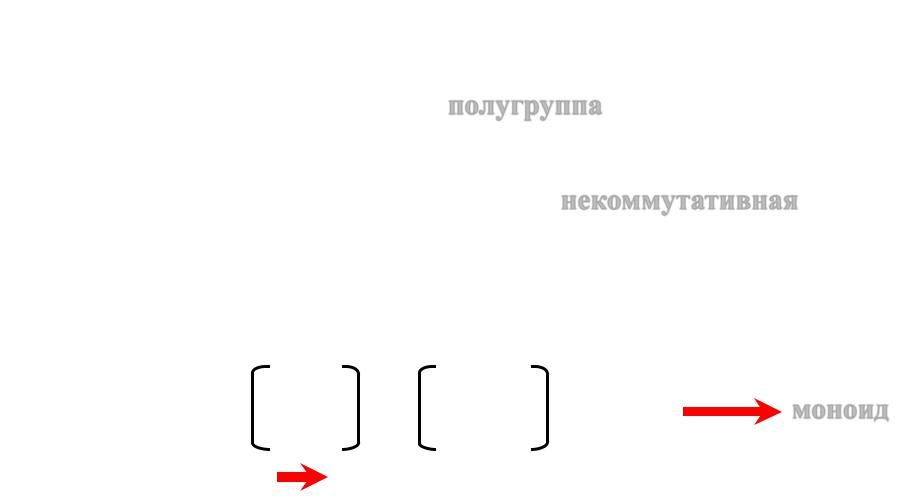
По построению: операция – ассоциативная. Общее количество преобразований множества M = { 1, 2, 3 } – 33 = 27

Множество всех преобразований T(M) = { α1, α2, … , α27 } в силу своей исчерпывающей полноты замкнуто относительно операции Δ, значит, алгебра [ T(M); ] - полугруппа

Видели на простейшем примере: возможно αΔβ βΔα, значит, в общем случае алгебра [ T(M); ] – некоммутативная

Опять же, в силу своей исчерпывающей полноты множества всех преобразований T(M) = { α1, α2, … , α27 }, в нём имеется, в том числе, тождественное преобразование

	Очевидно: αi		1	2	3	=	1	2	3	αi = αi	моноид
			1	2	3		1	2	3
					нет гарантии обратного преобразования
	Нет инъективности
			Итак, некоммутативный моноид преобразований
			конечного множества M = { 1, 2, 3 }

В T(M) построим подмножество T (M), замкнутое относительно

операции			:
α =	1	2	3		1	2	3	2	1	2	3
				β =
	1	2	2		3	3	2	γ = β =	2	2	3

δ = αΔβ =

1 2 3

3 3 3

Результат применения операции

			Правый операнд
	операнд		α	β	γ	δ	ζ
		α	α	δ	ζ	δ	ζ
		β	ζ	γ	β	δ	ζ
	Левый	γ	ζ	β	γ	δ	ζ
		δ	ζ	ζ	δ	δ	ζ
		ζ	ζ	ζ	ζ	δ	ζ

ζ = βΔα = 1	2	3
2	2	2

– в таблице Кэли:

Построена некоммутативная полугруппа преобразований множества М = { 1, 2, 3 } с

операцией и основным множеством Т (М) = { α, β, γ, δ, ζ }

			Правый операнд
	операнд		α	β	γ	δ	ζ	ε
		α	α	δ	ζ	δ	ζ	ε
		β	ζ	γ	β	δ	ζ	ε
	Левый
		γ	ζ	β	γ	δ	ζ	ε
		δ	ζ	ζ	δ	δ	ζ	ε
		ζ	ζ	ζ	ζ	δ	ζ	ε
		ε	ε	ε	ε	ε	ε	ε

Дополним Т (М) тождественным преобразованием

1 2 3

ε =

1 2 3

и включим в таблицу Кэли строку и столбец, получим моноид – полугруппу преобразований множества с нейтральным элементом

В связи с отсутствием инъективности обратное преобразование в общем случае не определено, поэтому требование из определения группы не выполнено