
- •1.Сходимость числового ряда
- •4. Признаки сравнения положительных рядов
- •Тогда ряд сходится или расходится одновременно с несобственным интегралом .
- •5. Знакочередующиеся ряды
- •6. Абсолютная и условная сходимость
- •7. Область сходимости функционального ряда
- •Теорема Абеля для степенных рядов
- •8. Радиус сходимости степенного ряда
- •Определение интервала сходимости
- •9. Почленное дифференцирование степенного ряда
- •Почленное интегрирование степенного ряда
- •10. Степенные ряды в окрестности произвольной точки.
- •11.Разложение элементарных функций в ряд Маклорена
- •15. Принцип умножения
- •16. Перестановки
- •Непосредственные следствия из аксиом
- •24. Схема равновозможных исходов
- •Алгоритм реализации схемы равновозможных исходов
- •Эмпирический закон больших чисел
- •25. Условная вероятность
- •26. Теорема умножения
- •27. Независимость событий
- •I. Независимость двух событий.
- •II. Независимость событий в совокупности.
- •30. Формула полной вероятности
25. Условная вероятность
Определение.Пусть при проведении испытаний число наступлений события
испытаний число наступлений события (то есть события
(то есть события вместе с событием
вместе с событием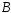 )
равно
)
равно ,
причем
,
причем наступило
наступило раз.Условной относительной частотой
события
раз.Условной относительной частотой
события
 при условии наступления события
при условии наступления события называется отношение
называется отношение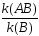 .
.
Обозначение
условной относительной частоты:
 .
Таким образом,
.
Таким образом, .
.
Теорема.Для условной относительной частоты справедлива формула:
 .
(10)
.
(10)
Определение.Пусть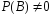 .
Условной вероятностью события
.
Условной вероятностью события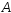 при условии наступления события
при условии наступления события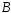 называется отношение:
называется отношение:
 .
(11)
.
(11)
26. Теорема умножения
Теорема (умножения).Если
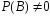 (так что существует условная
вероятность
(так что существует условная
вероятность
 ),
то для вероятности произведения событий
справедлива формула:
),
то для вероятности произведения событий
справедлива формула:
 .
(12)
.
(12)
Доказательство.Достаточно в формуле (11) обе части
равенства умножить на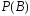 .
▄
.
▄
27. Независимость событий
I. Независимость двух событий.
Определение.События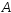 и
и называютсянезависимыми, если
вероятность произведения этих событий
равна произведению их вероятностей:
называютсянезависимыми, если
вероятность произведения этих событий
равна произведению их вероятностей:
 .
(14)
.
(14)
Таким образом, имеются две формы теоремы умножения:
1. Для произвольных событий:
 .
.
2. Для независимыхсобытий:
 .
.
Теорема (критерий
независимости двух событий).Пусть
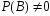 .
Для того, чтобы события
.
Для того, чтобы события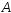 и
и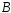 были независимы, необходимо и достаточно,
чтобы условная вероятность события
были независимы, необходимо и достаточно,
чтобы условная вероятность события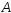 совпадала с его безусловной вероятностью:
совпадала с его безусловной вероятностью: .
.
28.Теорема
(независимость для противоположных
событий).Если события
 и
и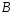 независимы, то независимы также пары
событий
независимы, то независимы также пары
событий
 и
и
 ,
,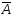 и
и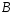 ,
, и
и .
.
Теорема (о
независимости от
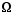 и
и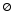 ).Любое событие
).Любое событие не зависит от достоверного события и
от невозможного события.
не зависит от достоверного события и
от невозможного события.
Доказательство.1. ,
так что
,
так что и
и независимы.
независимы.
2.
 ,
так что
,
так что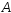 и
и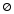 независимы. ▄
независимы. ▄
II. Независимость событий в совокупности.
Для трех и более
событий
 их взаимная независимость («независимость
в совокупности») означает не только то,
что любые два из них не влияют друг на
друга (попарная независимость):
их взаимная независимость («независимость
в совокупности») означает не только то,
что любые два из них не влияют друг на
друга (попарная независимость):
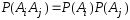 ,
(
,
( ),
(15)
),
(15)
но и что для любого подмножества из трех, четырех и т.д. событий этой совокупности вероятность произведения событий равна произведению их вероятностей:
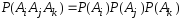 ,
(
,
( ),
(16)
),
(16)
 ,
(
,
( ),
(17)
),
(17)
и т. д. вплоть до условия
 .
(18)
.
(18)
Недостаточность попарных соотношений (15) для справедливости совокупности равенств (16)–(18) показывает
Пример С.Н.Бернштейна. Испытание: наугад бросается игральная кость, имеющая форму правильного тетраэдра, четыре грани которого имеют, соответственно, белую, синюю, красную и тройную бело-сине-красную (полосатую) окраску.
Рассмотрим события:
 — на выпавшей грани присутствует белый
цвет,
— на выпавшей грани присутствует белый
цвет,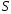 —
на выпавшей грани присутствует синий
цвет,
—
на выпавшей грани присутствует синий
цвет,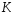 —
на выпавшей грани присутствует красный
цвет. По схеме равновозможных исходов
легко убедиться, что
—
на выпавшей грани присутствует красный
цвет. По схеме равновозможных исходов
легко убедиться, что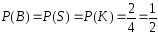 .
Далее, произведение любых двух из них
означает выпадение полосатой грани,
так что
.
Далее, произведение любых двух из них
означает выпадение полосатой грани,
так что .
Значит, условие (15) выполняется. В то же
время
.
Значит, условие (15) выполняется. В то же
время ,
и условие (16) не выполняется.
,
и условие (16) не выполняется.
30. Формула полной вероятности
Определение.События образуютполную группу, если
выполняются два условия: 1)в результате
испытания одно из них обязательно
наступает, то есть их сумма есть
достоверное событие:
образуютполную группу, если
выполняются два условия: 1)в результате
испытания одно из них обязательно
наступает, то есть их сумма есть
достоверное событие: ;
2) события попарно несовместны, то есть
;
2) события попарно несовместны, то есть при
при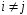 .
.
Теорема.Пусть выполняются два условия:
1. События
 («гипотезы») образуют полную группу.
(«гипотезы») образуют полную группу.
2. События
 имеют ненулевые вероятности:
имеют ненулевые вероятности: .
.
Тогда для всякого
события
 справедлива формула:
справедлива формула:
 ,
,
или в краткой записи:
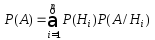 .
(19)
.
(19)
31. Формулы Бейеса
Теорема.Пусть
для событий
 («гипотез») и события
(«гипотез») и события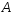 выполняются три условия:
выполняются три условия:
1. Гипотезы
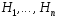 образуют полную группу.
образуют полную группу.
2. Гипотезы
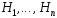 имеют ненулевые вероятности:
имеют ненулевые вероятности:
 .
.
3.
 .
.
Тогда при
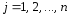 справедливы формулы:
справедливы формулы:
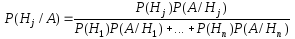
или в краткой записи:
 . (20)
. (20)
32. Схема независимых испытаний Бернулли
Определение.Испытания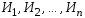 образуют относительно исхода
образуют относительно исхода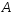 последовательность независимых испытаний
по схеме Бернулли, если выполняются два
условия:
последовательность независимых испытаний
по схеме Бернулли, если выполняются два
условия:
1. Исходы испытаний независимы в совокупности.
2. Вероятность
исхода
 во всех испытаниях одинакова и равна
во всех испытаниях одинакова и равна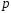 .
.
Терминология:
 — успех,
— успех, — вероятность успеха,
— вероятность успеха, — неудача,
— неудача, — вероятность неудачи.
— вероятность неудачи.
Теорема (о вероятности числа успехов).Справедлива формула:
 .
(21)
.
(21)
(Здесь
 – число сочетаний из
– число сочетаний из по
по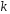 ;
см. п. 1.5).
;
см. п. 1.5).
33. Локальная теорема Лапласа
I. Дифференциальная функция Лапласа.
Определение.
Дифференциальной функцией Лапласаназывается функция .
.
График дифференциальной функции Лапласа («колокол») приведен на рис. 10.

Рис. 10.
Свойства функции
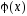 .
.
1. при всех
при всех .
.
2. —чётная функция, то есть
—чётная функция, то есть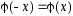 .
График функции симметричен относительно
оси ординат.
.
График функции симметричен относительно
оси ординат.
3. .
.
Стремление к нулю
в последнем пределе достаточно быстрое.
Так, с точностью до четырех знаков после
запятой
 .
.
Для отыскания
значений функции
 имеются таблицы и стандартные компьютерные
программы.
имеются таблицы и стандартные компьютерные
программы.
II. Предельное равенство.
Введём для
 испытаний по схеме Бернулли с вероятностью
успеха
испытаний по схеме Бернулли с вероятностью
успеха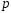 обозначения:
обозначения:
 ,
где
,
где
 – количество успехов (
– количество успехов (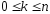 ),
),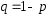 .
.
Теорема. Пусть
вероятность успеха
 в серии независимых испытаний по схеме
Бернулли удовлетворяет условию
в серии независимых испытаний по схеме
Бернулли удовлетворяет условию .
Тогда
.
Тогда
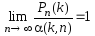 .
(24)
.
(24)
3.13. Интегральная теорема Лапласа
I. Интегральная функция Лапласа.
Определение. Интегральной функцией Лапласаназывается интеграл с переменным верхним пределом:
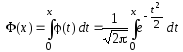 .
.
Для отыскания
значений функции
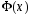 имеются таблицы и стандартные компьютерные
программы.
имеются таблицы и стандартные компьютерные
программы.
График интегральной
функции Лапласа приведен на рис. 11.
Геометрически
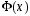 выражает площадь заштрихованной части
криволинейной трапеции на рис. 12.
выражает площадь заштрихованной части
криволинейной трапеции на рис. 12.
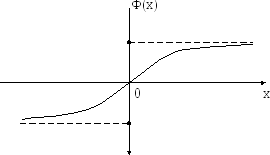
Рис. 11.




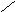







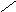



x
t
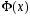 (x)
(x)
Рис. 12.
Свойства функции
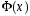 .
.
1.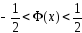 при всех
при всех
 .
.
2. – нечётная функция, то есть
– нечётная функция, то есть .
График
.
График
функции симметричен относительно начала координат.
 ;
;
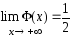 .
.
4. является производной для
является производной для
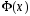 :
: .
.
5.Функция
 строго возрастает.
строго возрастает.
II. Предельное равенство.
Введём обозначение:
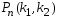 — вероятность того, что в серии из
— вероятность того, что в серии из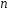 испытаний по схеме Бернулли число
успехов
испытаний по схеме Бернулли число
успехов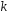 лежит в пределах:
лежит в пределах: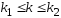 .
.
Пусть, как и в п.
3.12:
 — количество испытаний по схеме Бернулли,
— количество испытаний по схеме Бернулли, — вероятность успеха,
— вероятность успеха, .
.
Теорема. Пусть
для вероятности успеха
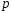 в серии независимых испытаний по схеме
Бернулли выполняется условие
в серии независимых испытаний по схеме
Бернулли выполняется условие .
Тогда для вероятности
.
Тогда для вероятности :
:


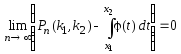 , (25)
, (25)
или, учитывая
определение функции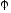 :
:
 . (26)
. (26)
