Методы и средства передачи информации (Лекция №9)

Методы и средства передачи информации

Лекционный курс

Лекция № 9

Содержание

1.Теорема Умова-Пойнтинга

2.Понятие вектора Пойнтинга

3.Анализ физических процессов передачи энергии в плоскопараллельных системах

1. Теорема Умова-Пойнтинга

Из уравнений Максвелла может быть получена основная теорема электромагнетизма, выражающая закон сохранения энергии электромагнитного поля. Теорема является одной из двух квадратичных форм (вторая форма называется леммой Лоренца) для системы этих уравнений.

Прежде запишем уравнения Максвелла в дифференциальной форме (т.е. с применение дифференциальных операторов).

Переход от интегрального представления уравнений Максвелла, справедливых для электродинамических систем конечных размеров (т.е. заданной области пространства со своими параметрами (электрофизическими свойствами) среды, поверхностями, ограничивающими исследуемое пространство, и системой источников поля) к дифференциальным уравнениям, описывающих связь составляющих поля в точке пространства, основан на применении теоремы Остроград- ского-Гаусса

∫ D dV = ∫D ds		(9.1)
V	S
и теоремы Стокса
∫[ B ]ds = ∫B dl ,		(9.2)
S	l

где − вектор Набла − формально введенное понятие (см. лекция № 8, п.3).

В результате замен интегралов по объему и интегралов по поверхности соответственно на интегралы по поверхности и интегралы по контуру в уравнениях Максвелла, исходя из равенства подынтегральных выражений:

∫[ H ]ds = ∫J э ds +				d	∫Dds ,	(9.3)
				d t
S	S				S
∫[ E ]ds = −		d	∫B ds ,			(9.4)
		d t
S			S
∫ DdV = ∫ρdV = Q ,						(9.5)
V	V
∫ B dV = 0 ,						(9.6)
V

уравнения Максвелла примут вид дифференциальных соотношений:

[ H ]= J

э

+

∂D

rot H = J

э

+

dD

,

(9.7)

∂t

d t

[ E ]= −

dB

,

или

rot E = −

dB

,

(9.8)

d t

d t

D =ρ,

div D =ρ,

(9.9)

B = 0 .

div B = 0 .

(9.10)

Заметим, что аналогично в дифференциальной форме представляется и уравнение непрерывности (1.5) с применением к нему уравнения Остроградско- го-Гаусса:

	div J п = −	d ρ	(9.11)
		d t

Еще раз отметим, название отражает не только вид операторов в уравнениях, но и тот факт, что соотношения справедливы в каждой точке пространства. В заключение заметим, что расчет электромагнитного поля в любой системе источников поля расположенных в некотором пространстве (в общем случае говорят в электродинамической системе) сводится к интегрированию уравнений Максвелла.

2

Обратимся к первому (9.7) и второму (9.8) уравнениям Максвелла в дифференциальной форме и, умножив первое уравнение на вектор Е, а второе – на вектор Н, и вычитая из второго уравнения первое, получим:

∂

εa E 2

µa H 2

2

ст

H rot E− E rot H = −

−

− σE

− J

E .

2

2

∂t

Используя равенство [E,H]= H[ ,E]− E[ ,H] (так как из векторного ана-

лиза следует, что [E,H]= H[ ,E]− E[ ,H] , где – векторный оператор), полу-

div[E,H]= −

∂

εa E

2

µa H

2

− σE 2

− JстE .

чим:

−

(9.12)

2

2

∂t

Проинтегрируем полученное выражение (9.12) по любому объему V и, применив теорему Остроградского – Гаусса, получим:

− ∫J

ст

∂

εa E

2

µa H

2

2

dv + ∫[E,H]n ds .

Edv =

−

(9.13)

∂t ∫

2

2

dv − ∫σE

V

V

V

S

Выражение (9.13) представляет теорему Умова-Пойнтинга о балансе мощ-

ностей электромагнитного поля. Левая часть выражения − мгновенная мощность, отдаваемая сторонними источниками тока, расположенными в объеме V (рис. 9.1). Первое слагаемое в правой части − мгновенная мощность, накапливаемая в объеме V, второе − мгновенная мощность, расходуемая на нагрев среды объеме

V, а третье − мгновенная мощность, излучаемая из этого объема через поверхность S , ограничивающую объем V, в окружающее пространство.

n

J ст

S V

Рисунок 9.1 − К теореме Умова-Пойнтинга

3

Подынтегральное выражение в последнем слагаемом, обозначаемое П = [E , H ] , представляет собой мгновенное значение вектора плотности потока

мощности через единичную площадку ds поверхности S , называется вектором

Пойнтинга.		Вектор Пойнтинга образует с векторами Е и Н правовинтвую сис-
тему. При		этом интеграл	∫[E, H]n ds ,	распространенный по замкнутой по-
			S
верхности		S, имеет физический смысл полной мощности, излучаемой из объе-
ма V. При этом, в случае			наложения,	например, электростатического поля на
магнитостатичское поле, вектор Пойнтинга					может иметь конечное значение
в некоторых точках объема, но при				этом	divП=HrotE - ErotH =0, так как
rot E = 0 и rot H = 0 , и, соответственно:
		∫[E ,H ]n ds = ∫div Пdv = 0,
		S	V

т.е. при такой системе полей излучения из объема нет.

При рассмотрении гармонических во времени колебаний, имея в виду, что негармонические колебания могут быть изучены разложением в ряд Фурье по гармоническим составляющим, применяют уравнения Максвелла в комплексной форме.

Обычно комплексная форма уравнений Максвелла образуется в результате формального осуществления Фурье преобразований уравнений Максвелла, записанных в виде дифференциальных соотношений. При этом, с учетом соответствия оператора d/dt во временнόй области − сомножителю iω (i−мнимая единица) в частотной области, уравнения (9.7)….(9.10) представятся в виде уравнений Максвелла в комплексной форме:

rot H = J э + iωD ,	(9.11)
rot E = −iωB ,	(9.12)
div D =ρ,	(9.13)
div B = 0 .	(9.14)

При этом и баланс мощностей можно представить в частотной области.

4

Для этого необходимо в комплексной форме уравнений Максвелла

rot H = J э + iωD =iωε a E+ J ст ,
rot E = −iωµ a H ,	(9.15)

где ε a − комплексная абсолютная диэлектрическая проницаемость, введенная со-

	гласно формуле iωε a	=iωε a + σ в виде ε a	= ε a	+	σ		, составить уравнение,
					iω

комплексно сопряженное с первым уравнением в системе (9.15):

rot H = −iωε a E+ σE + J ст .

Умножив это уравнение на вектор Е , а второе уравнение (9.15) на H и вычитая из второго уравнения первое, получим уравнение аналогичное (9.12), но в комплексной форме:

			ст E .
div [E ,H ]= −iωµ a H H +iωε a E E −σE E −J				(9.16)

Интегрирую выражение (9.16) по произвольному объему и принимая во внимание теорему Остроградского-Гаусса, получим

−

1

ст

Edv =iω

1

1

1

∫J

∫

µ a H H −ε a E E dv +

∫σE Edv +

∫ E , H ds , (9.17)

2 V

2 V

2 V

2

S

где

1

= П – вектор Пойнтинга в комплексной форме.

2

Е, H

Уравнение (9.17) представляет собой теорему Умова-Пойнтинга в комплексной форме, т.е. в частотной области. Действительная часть вектора Пойнтинга в (9.17) определяет его среднее за период колебания значение. В выражении (9.17) аналогично (9.13) левая часть определяет мощность, отдаваемую источниками электромагнитного поля. Первое слагаемой в правой части – реактивная мощность, которая накапливается в объеме V , второе – активная мощность, которая теряется на нагрев среды в объеме, третье – мощность, которая излучается через поверхность S, ограничивающую объем V. В общем случае третье слагаемое является комплексной величиной. Комплексной является также и левая часть выражения.

5

Заметим, что физическая интерпретация каждого из слагаемых в выражениях (9.13) и (9.17) кроме последнего слагаемого соответствует опытным данным, полученным при расчете и анализе полей и энергии поля в простейших системах электростатических и стационарных полей. Осознание физического смысла последнего слагаемого пришло после изучения этой квадратичной формы для уравнений Максвелла.

Теорема Умова-Пойнтинга позволяет производить оценку мощности излучаемой электродинамической системой в окружающее пространство, что важно при проектировании антенных систем и решении задач электромагнитной совместимости различных технических средств, а также – энергию, накапливаемую и теряемую в системе.

2. Понятие вектора Пойнтинга

Осознание физического смысла формально полученного вектора Пойнтинга пришло после изучения квадратичной формы для уравнений Максвелла, названной теоремой Умова-Пойнтнга. Вектор Пойнтинга – феноменологическое понятие, т.е. понятие, которое подтверждается анализом физического смысла других составляющих выражения теоремы Умова-Пойнтинга, а также косвенными данными, которые интерпретируются в нашем сознании определенным образом. Интерпретация основана на проведении измерений мощности передаваемой по линиям передачи и по свободному пространству, при излучении мощности антеннами.

Кроме физического смысла вектора Пойнтинга, связанного с законом сохранения энергии, анализ распределения плотности потока мощности, т.е. вектора Пойнтинга, в пространстве вокруг излучателя или в сечениях линии передачи позволяет осознать суть процессов, происходящих при передаче мощности. Это представляет важное мировоззренческое значение.

3.Анализ физических процессов передачи энергии

вплоскопараллельных системах

Плоскопараллельными системами называют системы, формирующие плоскопараллельное поле. Основное внимание при изучении таких систем уделяется

6

двухсвязанным линиям передачи (в основном – энергии в силовых цепях и информации в линиях связи или иначе – в «слаботочных» цепях). В основе расчета передачи мощности в двухсвязанных линиях, к которым относятся двухпроводные линии, образованные парой параллельных проводов, и коаксиальные линии, образованные центральным проводником – жилой (как правило круглого сечения) и окружающей её, симметрично размещенной цилиндрической оболочкой, лежит положение относительно характера поля в системе, соответствующего, так называемой, зоне индукции (или ближней зоне), подробно рассматриваемых ниже в нашем курсе. Сейчас лишь заметим, что это понятие соответствует соотношению l << λ между поперечными размерами l системы проводников и длиной волны λ в реальных системах выполняется до весьма высоких частот (до единиц гигагерц). В зоне индукции структуру поля в таких линиях можно представить в виде независимых электрического и магнитного полей. При этом электрическое поле представляет собой квазистатическое поле, а магнитное поле – квазистационарное магнитное поле. Тогда при расчете мощности (т.е. вектора Пойнтинга) в двусвязанных системах можно просто (формально) применить выражения для электростатического и для стационарного магнитного полей, предполагая, что это не независимые поля (хотя они определены именно в такой системе уравнений), а переменные поля, удовлетворяющие полной системе уравнений Максвелла (т.е. системе, учитывающей связь между составляющими электромагнитного поля).

Рассмотрение вопроса передачи мощности по двухсвязанным системам проведем на примерах расчетов двухпроводной линии и коаксиального кабеля, однако сначала остановимся на рассмотрении процесса в прямолинейном проводе, по которому идет постоянный ток.

Пусть для простоты провод имеет круглое сечение, радиус которого а (рис. 9.2). Запишем вектор Пойнтинга в такой системе. Для этого определим век-

тора поля, формируемого током в проводе. Ток создает вокруг провода (r≥ a)

7

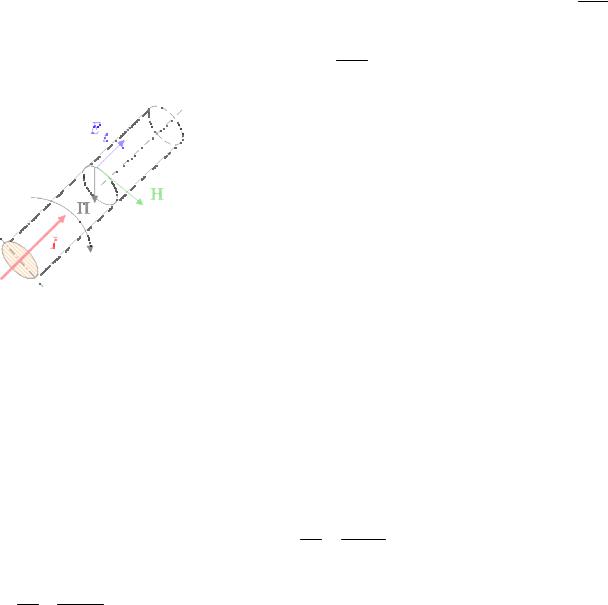
магнитное поле, которое согласно закону полного тока и симметрии задачи имеет только азимутальную (относительно оси провода) компоненту Hα = 2πI r ,

которая на поверхности провода равна Hα = 2πI a .

Рисунок 9.2 – Прямолинейный провод с постоянным током

Электрическое поле на поверхности провода имеет две составляющие. Нормальная к поверхности провода составляющая напряженности электрического поля выражается через поверхностную плотность свободного заряда, которую в такой постановке задачи определить невозможно (так как не определено положение обратного провода). Тангенциальная составляющая определяется в соответствии с дифференциальной формой закона Ома. С учетом направления тока I в проводе и, соответственно, направления его объемной плотности, при вы-

боре оси z вдоль оси провода Ez = Jσz = σπIr 2 , а на поверхности провода

Ez = Jσz = σπIa2 .

Откуда на поверхности провода вектор Пойнтинга

I

I

I

2

ПS =[E,H]=r0 (Ez Hα )=r0

=r0

=r0

Пr

,

2

2

σπa

σ2π

a

3

2πa

а поток вектора Пойнтинга, направленный по радиусу внутрь провода

− ∫ПS ds = −∫[r0 (Ez Hα )](- r0 )ds = ∫(Ez Hα )ds =

S	S			S
2πl	I 2			I 2		I 2l	2	= = RI	2	,
= ∫∫	2 3 adαdl =			2 3 a 2πl =
0 0 σ2 π a			σ2 π a			σπa

8

	где R =	l	– сопротивление провода длиной l. Т.е. сопротивление провода
		σπa2

(понятие, используемое в электротехнических моделях – принципиальных или эквивалентных схемах – определяется потоком мощности, направленным внутрь проводника и рассеиваемое в нем в тепло).

Теперь рассмотрим передачу энергии по длинной двухпроводной линии. В такой полевой системе поле плоскопараллельное. Для анализа передачи энергии в такой структуре необходимо знать распределение в поперечном сечении линии вектора Пойнтинга. Для анализа распределения в поперечном пространстве двухпроводной линии вектора Пойнтинга необходимо знать структуру полей в поперечном сечении.

Из предыдущей лекции мы знаем, что силовые линии электрического поля образуют окружности, опирающиеся на оси (в плоскости поперечного сечения − это точки с τ + и τ − ). Можно показать, что линии напряженности магнитного поля тоже образуют в плоскости поперечного сечения окружности. Для этого достаточно проанализировать связь между векторами напряженности магнитного поля и вспомогательным понятием векторного потенциала.

Вспомогательный вектор А вводится равенством

µ 0 µ r H = rot A ,

(9.18)

где А – векторный потенциал, который, как мы видели в предыдущей лекции, «недоопределён», так как его дивергенция не задана, т.е. не заданы его истоки.

Для применения введенного понятия необходимо установить его связь с источниками поля. Связь устанавливается следующей последовательностью действий.

Из второго уравнения Максвелла с подстановкой вектора магнитной индукции через векторный потенциал получим уравнение

	rot E = −	∂	(rot A ),	(9.19)
		∂t

которое представим в виде

9

	E +	∂A		=0.	(9.20)
rot
		∂t

Из выражения (9.20) следует, что поле вектора E + ∂∂At потенциально, так

как ротор градиента любой скалярной функции равен нулю ([ ( ϕ )]= 0 ввиду колинеарности векторов и ϕ ). Поэтому можно считать, что:

	E +	∂A	= −grad ϕ ,	(9.21)
		∂t

где φ – некоторая скалярная функция, называемая также как и в электростатике скалярным потенциалом. Причем знак минус в уравнении (9.21) взят для соответствия между скалярным потенциалом электростатического поля, где он имеет физический смысл убывания энергии при действии силового поля.

Из равенства (9.21) следует, что вектор напряженности электрического поля можно представить через потенциалы в виде:

	E = −	∂A	−grad ϕ.	(9.22)
		∂t

Подставив выражения (9.18) и (9.22) для векторов Н и Е в уравнения Максвелла (9.11) и (9.13), получим:

rot ( rot A )=µ a J −ε a µ a ∂ 2 A −ε a µ a				∂	grad ϕ,			(9.23)
			∂t 2	∂t
div ∂A	+ div grad ϕ= −	ρ	,					(9.24)
∂t		ε a
где µ a =µ 0 µ r и ε a	= ε 0 ε r − абсолютные магнитная и диэлектрическая прони-
цаемости среды.
Преобразуем выражение (9.23), раскрыв понятие rot rot А, как двойное век-
торное произведение:
grad div A − 2 A =µ a J −ε a µ a ∂ 2 A −ε a µ a						∂	gradϕ,
			∂t 2			∂t

где, поменяв местами слагаемые, запишем:

10