Математические основы моделирования сложных физических систем

3.2. Получение слабой формы

Запишем интеграл невязки задачи (3.1), (3.2)

1

0

	d	D(x)	du	C(x)	du	A(x)u q(x) dx = 0.	(3.3)
	dx		dx		dx

Затем выполним в (3.3) интегрирование по частям. Получим:

		D(x)	du		1
			dx 0							(3.4)
	1
				du			d (x)		du
		D(x)						(x) C(x)		A(x)u q(x) dx = 0.
	0			dx			dx		dx

Учтем граничное условие (3.2) и получим окончательно интегральное уравнение эквивалентное исходному дифференциальному уравнению (3.1) c

граничными условиями (3.2):

1

au 10

0

D(x)	du		d (x)	(x) C(x)	du	A(x)u q(x) dx = 0. (3.5)
	dx		dx		dx

Выберем пробные функции в виде "домиков" (1.28) и получим с помощью метода Галеркина матричное уравнение. Для этого подставим аппроксимацию искомого решения (1.26) и ее производную (1.32) в

интегральное уравнение (3.5) и получим матричное уравнение размерности nxn , i -тая строка которого имеет вид:

aui in

aui i1

xi

hip

n

d

d j

d

i

D(x)u

(x)C(x)u

j

(x) A(x)u

(x) dx

(3.6)

j

i

j

i

j

j

dx

dx

dx

xi

him

j=1

xi

hip

=

i (x)q(x)dx

xi

him

Здесь вычисление интегралов производится по окрестности i

- того узла,

him

40

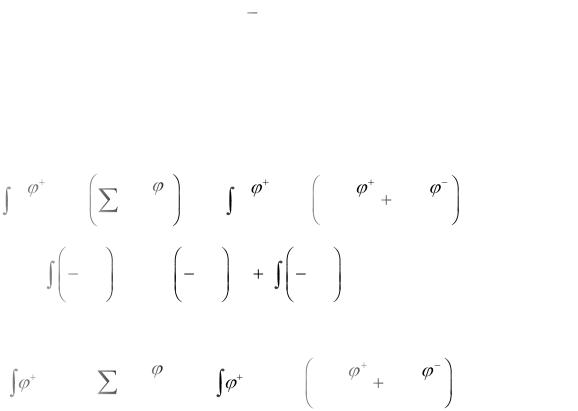
- шаг назад из i	- того узла, hip	- шаг вперед, причем шаги назад из первого
узла и вперед	из последнего	узла не делаются (рисунок 1.4), поэтому
h1m = 0, hnp = 0 .

3.3. Матричные коэффициенты на сетке узлов с изменяющимся шагом При интегрировании по окрестности i - того узла учтем, что сетка

узлов может быть адаптирована к задаче, и шаги вправо him и влево hip от i -

того узла могут быть разными. Вычислим матричные коэффициенты построчно. При вычислении коэффициентов удобно пользоваться для наглядности рисунком 1.4.

Получим отличные от нуля коэффициенты первой строки матрицы f1 j .

Вклад в f1 j дают только столбцы с j = 1 и j = 2 . Граничные условия дают

вклад только в коэффицент f11 , равный au11.

Нижний предел в интегралах положен равным нулю, а верхний предел в интегралах обозначен как шаг вперед из первого узла с координатой x = 0 .

Выполним интегрирование каждого члена суммы под знаком интеграла отдельно. Вычислим первый интеграл в выражении (3.6):

h1 p

d

2

d j

h1 p

d

d

d

1

D(x)

u

dx =

1

D(x) u

1

u

2

dx =

0

dx

1 j

dx

0

dx

11

dx

12

dx

j=1

h1 p

1

1

h1 p

1

1

D(x)u

dx

D(x)u

dx.

0

h

11

h

0

h

12 h

1 p

1 p

1 p

1 p

Вычислим второй интеграл в выражении (3.6):

h1 p	2	d			h1 p	d 1		d 2
	1 (x)C(x) u1 j		j	dx =	1 (x)C(x) u11		u12		dx =
0		dx				dx		dx
	j=1				0

41

h1 p		1		h1 p		1
	(x)C(x)u		dx		(x)C(x)u		dx.
		h				h
1	11			1	12
0		1 p		0		1 p

Вычислим третий интеграл в выражении (3.6):

h1 p	2	h1 p
	1 (x) A(x) u1 j j (x) =	1 (x) A(x) u11 1 (x) u12 1 (x) dx.
0	j=1	0

Таким образом, отличные от нуля коэффициенты первой строки выражаются через интегралы по окрестности первого узла [0, h1 p ] и имеют вид:

1

h1 p

1 h1 p

h1 p

(3.7)

f11 =

a

D(x)dx

1 (x)C(x)dx

1 (x) A(x) 1 (x)dx;

h2

h

1 p

0

1 p

0

0

1 h1 p

1 h1 p

h1 p

(3.8)

f12 =

D(x)dx

1 (x)C(x)dx

1 (x) A(x) 2 (x)dx.

h2

h

1 p 0

1 p 0

0

Получим отличные от нуля коэффициенты последней строки матрицы

fnj . Вклад в

fnj

дают только столбцы с j = n

1 и

j = n (рисунок 1.4

(в)).

Граничные условия дают вклад только в коэффицент

fnn - этот вклад равен

aunn.

Верхний предел в интегралах положен равным xn , а нижний предел в интегралах обозначен как шаг назад из этого последнего узла. Вычислим первый интеграл в выражении (3.6):

xn

d n

n

d

D(x)unj

j

dx =

dx

dx

xn hnm

j=n 1

xn

d n

d n 1

d n

D(x) u

u

dx =

n,n 1

nn

dx

dx

dx

xn hnm

42

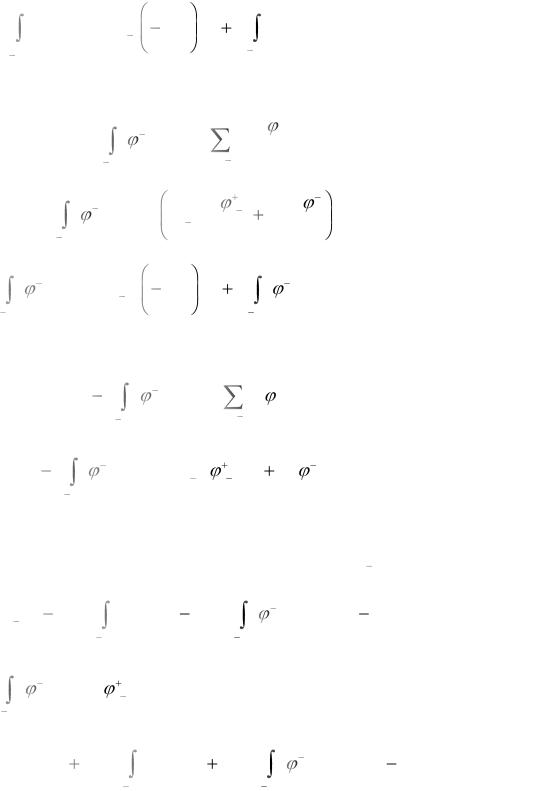
xn	1		1			xn	1			1
		D(x)u		dx				D(x)u			dx.
	h		h				h		nn h
		n,n 1
x	nm		nm		x	h	nm			nm
n h					n	nm
nm

Вычислим второй интеграл в выражении (3.6):

xn

n

d j

n (x)C(x)

unj

dx =

dx

xn hnm

j=n 1

xn

d

d n

n (x)C(x) un 1,n

n 1

unn

dx =

dx

dx

xn hnm

xn

1

xn

1

n (x)C(x)un 1,n

dx

(x)C(x)unn

dx.

h

n

h

x

h

x

h

nm

nm

n

nm

n

nm

Вычислим третий интеграл в выражении (3.6):

xn	n
n (x) A(x)	unj j (x) =
xn hnm	j=n 1
xn
n (x) A(x) un 1,n n 1(x) unn n (x) dx.
xn hnm

Таким образом, отличные от нуля коэффициенты последней строки выражаются через интегралы по окрестности n - го узла [xn 1, xn ] и имеют вид

1

xn

1

xn

fn,n 1 =

D(x)dx

n (x)C(x)dx

h2

h

nm x h

nm x

h

n

nm

n

nm

xn

n (x) A(x)

n 1(x)dx;

(3.9)

xn hnm

1

xn

1

xn

fnn = a

D(x)dx

n (x)C(x)dx

h2

h

nm x

h

nm x

h

n

nm

n

nm

43

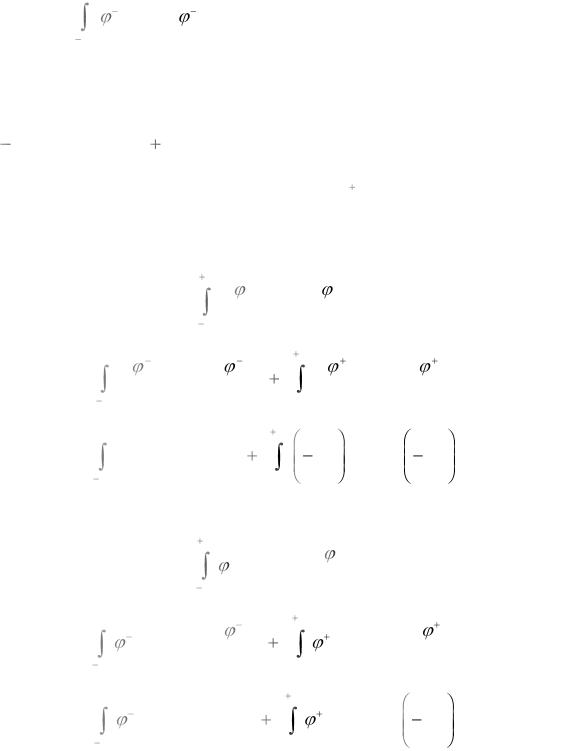
xn

n

xn hnm

(x) A(x) n (x)dx.

(3.10)

Вычислим коэффициенты в главной диагонали. Граничные условия не

дают вкладов в эти коэффициенты.

Вклад в

fij дают только столбцы с

j = i 1, j = i и

j = i

1 (рисунок

1.4 (б)). Коэффициенты вычисляются

интегрированием по отрезкам

[xi?1, xi ] и

[xi , xi 1] . Чтобы подчеркнуть, что

вычисляются коэффициенты i

- той стоки,

пределы в интегралах обозначены

как шаг назад или шаг вперед из i

- того узла. Вычислим первый интеграл

xi hip

d i

D(x)u

d i

dx =

xi

dx

ii

dx

him

xi

d i

d i

xi

hip

d i

d i

D(x)u

dx

D(x)u

dx =

xi

him

dx

ii

dx

xi

dx

ii

dx

xi

1

1

xi hip

1

1

D(x)u

dx

D(x)u

dx.

x

h

h

ii

h

x

h

ii

h

im

im

ip

ip

i

im

i

Вычислим второй интеграл в выражении (3.6)

xi

hip

d i

(x)C(x)u

dx =

xi

i

ii

dx

him

xi

d i

xi

hip

d i

(x)C(x)u

dx

(x)C(x)u

dx =

xi

him

i

ii

dx

xi

i

ii

dx

xi

1

xi

hip

1

(x)C(x)u

dx

(x)C(x)u

dx.

h

h

i

ii

i

ii

x

h

im

x

ip

i

im

i

Вычислим третий интеграл в выражении (3.6)

44

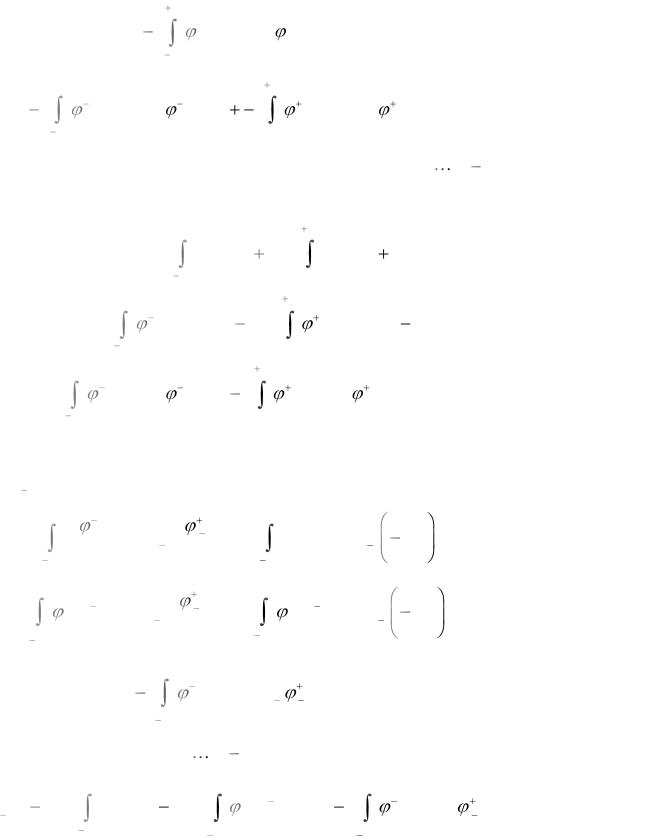
xi

hip

i (x) A(x)uii i (x)dx =

xi

him

xi

xi

hip

i (x) A(x)uii

i (x)dx

i (x) A(x)uii i (x) = dx.

xi him

xi

Таким образом, коэффициенты главной диагонали для i = 2,3, , n

1 имеют

вид:

1

xi

1

xi hip

fii =

D(x)dx

D(x)dx

h2

h2

im x

h

ip

x

i im

i

1

xi

1

xi

hip

i (x)C(x)dx

i (x)C(x)dx

(3.11)

him x

hip

h

x

i

im

i

xi

xi hip

i (x) A(x) i (x)dx

i (x) A(x) i (x) = dx.

xi him

xi

Вычислим коэффициенты под главной диагональю интегрированием по отрезкам [xi 1, xi ] :

xi

d i

d i 1

xi

1

1

D(x)u

dx =

D(x)u

dx.

x

h

dx

i,i 1

dx

x

h

h

i,i 1

h

im

im

i

im

i

im

xi

d i 1

xi

1

(x) C(x)u

dx =

(x) C(x)u

dx.

x

i

i,i 1

dx

x

h

i

i,i 1

h

im

i him

i

im

xi

i (x) A(x)ui,i 1 i 1(x)dx.

xi

him

Таким образом, для строк i = 2,3,

, n 1 получаем

1

xi

1

xi

xi

fi,i 1 =

D(x)dx

i (x)

C(x)dx

i (x) A(x) i 1(x). (3.12)

h2

h

im x

h

im x

him

x

i

im

i

i him

45

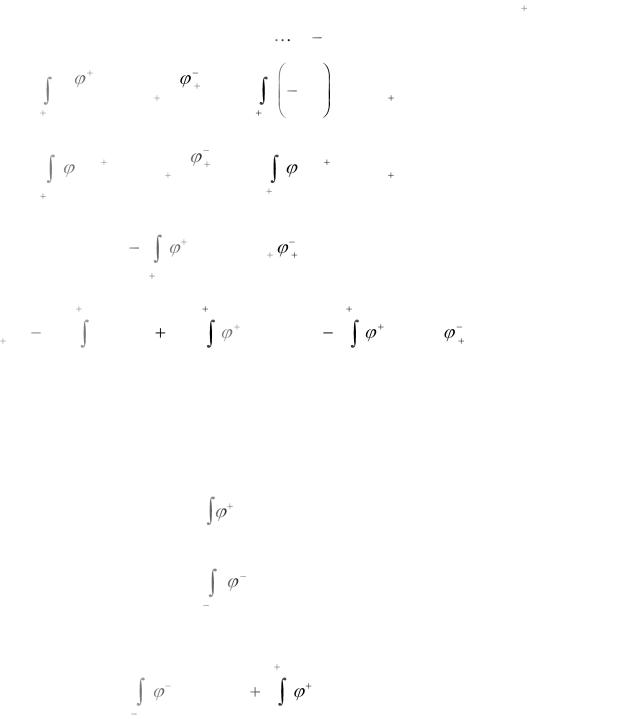
Вычислим коэффициенты над главной диагональю по отрезкам [xi , xi 1] .

Аналогично предыдущему для строк i = 2,3,

, n

1 получаем:

xi

d i

d

xi

1

1

D(x)u

i 1

dx =

D(x)u

dx.

x

h

dx

i,i 1

dx

x h

h

i,i 1 h

ip

ip

i

ip

i

ip

xi

d i 1

xi

1

(x) C(x)u

dx =

(x) C(x)u

dx.

x

i

i,i 1

dx

x

h

i

i,i 1 h

ip

i h

i

ip

im

xi

i (x) A(x)ui,i 1 i 1 (x)dx.

xi hip

1 xi hip

1 xi hip

xi hip

(x) A(x) i 1(x). (3.13)

fi,i 1 =

D(x)dx

i (x)C(x)dx

i

h2

h

ip x

ip

x

x

i

i

i

Правая часть системы уравнений (3.6) при произвольной нагрузке q(x)

и c меняющимся шагом дискретизации для первого и последнего узлов дается интегралами:

h1 p
Q1 =	1 (x)q(x)dx,	(3.14)
	0
	xn
Qn =	n (x)q(x)dx.	(3.15)
xn	hnm

Правая часть для внутренних узлов с номерми 1 < i < n дается интегралами

	xi	xi hip
Qi =	i (x)q(x)dx	i (x)q(x)dx.	(3.16)
xi	him	xi

В линейном дифференциальном уравнении коэффициенты уравнения зависят от координаты x , но не от самого искомого решения. В слабой форме матричные коэффициенты в этом случае находятся интегрированием функциональных коэффициентов уравнения по окрестности узлов, и таким

46

образом, коэффициенты усредняются по окрестности узла. Это расширяет класс решаемых задач по сравнению с коэффициентной формой, поскольку теперь коэффициенты могут быть кусочно непрерывными.

Такое интегрирование можно выполнить аналитически, если коэффициенты заданы в аналитическом виде, или численно. В первом случае программа будет предназначена для конкретной задачи и будет работать быстро, так как интегрировать функциональные коэффициенты в окрестности каждого узла не потребуется. Во втором случае функциональные коэффициенты уравнения можно задавать на входе программы, но время счета будет значительно большим, чем в первом случае.

Матрица по-прежнему оказывается ленточной, и каждое уравнение связывает не более трех неизвестных в соседних узлах. Для неравномерной сетки с изменяющимся шагом дискретизации матрица получается несимметричной, в отличие от случая равномерной сетки с постоянным шагом дискретизации.

3.4. Пример вычислительной программы

В Приложении приведен текст вычислительной программы fem3.cpp,

написанной на языке С++, в котором решается задача (3.1), (3.2) о

стационарной одномерной диффузии в составном стержне. Функциональные коэффициенты задаются кусочно постоянными функциями и скачком меняются на границах раздела. Источник частиц (тепла) - линейная функция.

В программе использован решатель системы линейных алгебраических уравнений методом разложения на нижнюю и верхнюю треугольные матрицы с выбором главного элемента для уменьшения ошибки. Проверку решения можно выполнить, написав программу, в которой полученное решение подставляется в исходное уравнение и выполнятся его численное

47

дифференцирование.

4. ДИФФУЗИЯ ЭЛЕКТРОНОВ В МНОГОСЛОЙНОЙ СТРУКТУРЕ

4.1. Классическая и обобщенная постановка задачи Диффузия электронов при бомбардировке пучком электронов мишени,

состоящей из нескольких слоев с различным химическим составом и плотностью описывается параболлическим уравнением смешанного типа с граничными и начальными условиям [1].

Роль времени в этом уравненнии играет потерянная энергия.

Обобщенное решение смешанной задачи для параболического уравнения В конечной пространственной области Rn с кусочно-гладкой границей рассматривается уравнение

u(x,t)

n

u(x,t)

K (x,t)

=

A (x,t)

t

xi

i

xi

i=1

n

u(x,t)

B (x,t)

G(x,t)u(x,t) F (x,t).

(4.1)

i

xi

i=1

По

отношению к переменной

t

все

коэффициенты непрерывны,

а

по

отношению к пространственным переменным удовлетворяют условиям

K ,B,G,F C(

), A C1(

), K > 0,A > 0,G > 0,

(4.2)

где

=

.

Считаем, что u(x,t) является

непрерывно дифференцируемой по

t

и

принадлежит классу C2 ( )

C1(

)

по переменным x . На границе заданы

краевые условия третьего рода

		n				u(x,t)
	C(x ,t)u(x,t)		n (x )D (x ,t)					= E(x ,t), x	,	(4.3)
			i	i		xi
		i=1
где u(x,t)	- след функции u(x,t) на поверхности							и
					48

C(x ,t), Di (x ,t), E(x ,t)		C( ), C(x ,t) 0,			(4.4)
и ni (x ) - компоненты орта внешней нормали к поверхности.					При t = 0
задано начальное условие
					(4.5)
u(x,0) = u0 (x), x		, u0 (x) C( ).
При сделанных предположениях решение этой задачи существует и
единственно [2], с.32.
Если коэффициенты не удовлетворяют необходимым					условиям

гладкости, то задачу следует трактовать в обобщенном смысле, считая

коэффициенты и решение элементами обобщенных функциональных классов

с соответствующим обобщенным толкованием производных. В такой постановке самыми естественными являются соболевские классы Wpm .

Обобщенное решение удовлетворяет некоторому интегральному

тождеству. Чтобы получить это тождество, умножим уравнение (4.1) на

функцию

(x)

W 1 (

) и проинтегрируем полученное равенство по области

2

. Используя формулу Остроградского –Грина, получаем

u

n

u

n

u

dx K

= dx A

dx

B

dx

Gu F

t

i=1 i

xi

xi

i=1

i

xi

(4.6)

n

u

d

i=1 ni (x ) Ai

.

xi

Обобщенным решением задачи (4.1),

(4.3),

(4.5)

называется функция

u(x,t)

W 1(

) ,

удовлетворяющая тождеству (4.6)

для

всех u(x,t) W 1

( ) ,

2

2

(x)

W 1(

) .

2

Пусть область

представляет собой параллелепипед

=

n

i=1 i , i = xi , xi

Определим грани параллелепипеда

49