1.3. Операции над матрицами

Суммой матриц иназывается такая матрица,

элементы которой равны сумме соответствующих элементов матриц A и B , т. е.

(1.19)

Складывать можно только матрицы одинакового размера.

Произведением числа на матрицуназывается такая матрица,

элементы которой вычисляются по формуле:

(1.20)

Матрица называется противоположной матрице

Разность матрицможно определить так:

Операции сложения матриц и умножения матрицы на число удовлетворяют следующим свойствам:

1) 5)

2) 6)

3) 7)

4) 8)

где матрицы;числа.

Пример 3. Даны матрицы ;. Вычислить матрицу.

Решение.

.

Операция умножения матрицы А на матрицу В возможна только тогда,

когда число столбцов первой матрицы, т. е. А, равно числу строк второй матрицы, т. е. В (но не наоборот!).

Произведением матрицы на матрицу , гденазывается такая матрица, элементы которой вычисляются по формуле:

(1.21)

Обратите внимание на то, что в матрице С получилось столько строк, сколько их имела матрица А, и столько столбцов, сколько их было в матрице В.

Пример 4. Даны матрицы ;. Найти матрицу

Решение.

Умножение матриц удовлетворяет следующим свойствам:

1) 4)

2) 5)

3) 6)

если, конечно, написанные суммы и произведения матриц имеют смысл.

Матрицы иназываются перестановочными, еслинапример, как видно из указанных выше свойств, матрицыиа такжеиперестановочны.

Замечание: в качестве упражнения докажите, что, например, матрицы

и не являются перестановочными.

1.4. Обратная матрица и ее вычисление

Квадратная матрица называется вырожденной, или особенной, если , иневырожденной, (неособенной), если .

Обратной к квадратной матрице А произвольного порядка называется квадратная матрица такого же порядка, что и А, обозначаемая через , которая удовлетворяет условию:

(1.22)

где Е – единичная матрица такого же порядка, что и А.

Обратная матрица существует только для невырожденной матрицы А.

Если матрица А имеет вид

(1.23)

то обратная матрица

(1.24)

где – алгебраические дополнения к элементам матрицы А.

Пример 5. Найти матрицу, обратную к матрице и сделать проверку.

Решение.

Значит, матрица А – невырожденная и обратная ей матрица существует. Найдем алгебраические дополнения:

;

;

Следовательно, .

Проверка.

1.5. Ранг матрицы

Рангом матрицы произвольного размера называется наибольший из порядков ее миноров, отличных от нуля, он обозначается через r(A).

Матрица имеет ранг r, если по крайней мере один из ее миноров r-го порядка отличен от нуля, а все миноры болеет высоких порядков, если они существуют, равны нулю.

Матрица будет нулевого ранга, если все ее элементы равны нулю. Например, для матрицы r(A) = 2, так как существует минор второго порядка а для матрицы ранг r(B) = 1, так как все миноры второго порядка равны нулю, но в матрице В есть элементы (миноры первого порядка), отличные от нуля. Следует отметить, что для обеих матриц миноры больше второго порядка не существуют, так как в матрицах по две строки.

Рассмотрим способ определения ранга матрицы А, который заключается в применении так называемых элементарных преобразований, не меняющих ранга матрицы; получаемые при этом матрицы называются эквивалентными.

Обозначение эквивалентных матриц и

К элементарным преобразованиям матрицы относится любая из следующих операций:

1) перемена местами любых двух строк (столбцов);

2) умножение каждого элемента произвольной строки (столбца) на один и тот же отличный от нуля множитель;

3) вычеркивание строки (столбца), целиком состоящей из нулей;

4) прибавление к элементам произвольной строки (столбца) соответствующих элементов другой строки (столбца), умноженных на произвольное число.

Путем элементарных преобразований любую ненулевую матрицу можно привести к матрице вида:

.(1.25)

Ранг матрицы (1.25) равен количеству единиц, стоящих на главной диагонали, так как минор

(1.26)

а все миноры более высоких порядков равны нулю, поскольку они содержат обязательно строку, или столбец, целиком состоящую из нулей. Действительно,

применив для их вычисления метод разложения определителя по элементам такой строки (столбца), получим величину определителя, равную нулю.

Пример 6. Вычислить ранг матрицы

Решение.

Для нахождения ранга матрицы переставим в ней первый и второй столбцы, а затем, умножая первую строку на , получаем:Прибавляя к третьему столбцу полученной матрицы удвоенный первый столбец, имеем: .Умножая последовательно первую строку на 4, (– 1), (– 5), (– 3) и прибавляя соответственно ко второй, третьей, четвертой и пятой строкам, получаем: .Далее, умножая вторую строку на (–1)и вычитая из третьего столбца утроенный второй, имеем: 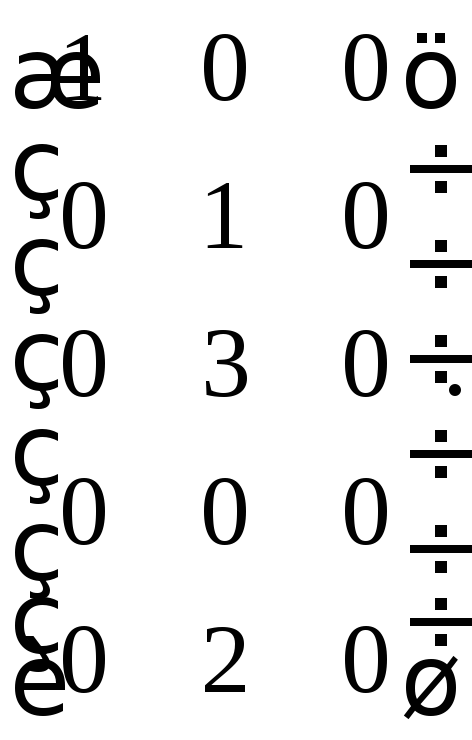Наконец, умножая последовательно вторую строку на (–3) и (–2) и прибавляя соответственно к третьей и пятой строкам, получим матрицу вида: Ранг полученной матрицы равен 2.