(по цифровому вещанию) Dvorkovich_V_Cifrovye_videoinformacionnye_sistemy

Глава 7. Групповое кодирование изображений

ляющая характеризует вклад соответствующей спектральной (базисной) функции в энергию исходного изображения.

При такой трактовке понятие частоты можно обобщить так, чтобы оно было применимо не только к косинусам и синусам, но и к другим функциям, на которых основываются преобразования.

Наглядное представление об унитарных преобразованиях изображений можно получить, рассматривая такое преобразование как поворот многомерной системы координат, при котором область возможных изменений векторов максимально сжимается («компрессируется»).

Еще одна возможность интерпретации преобразований заключается в том, что преобразование F (m1, m2) в X(n1, n2) можно представить как способ представления изображения в виде набора двумерных функций B(n1, n2; m1, m2), каждая из которых соответствует точке (m1, m2) плоскости обобщенных частот. В подобной интерпретации ядро B(n1, n2; m1, m2) называется двумерной базисной функцией, а коэффициент F (m1, m2) указывает «вес» этой базисной функции, необходимый для получения рассматриваемого изображения.

Обычно при анализе изображений используют квадратные блоки изображений размером N × N .

7.1.1. Дискретное преобразование Фурье

Дискретное двумерное преобразование Фурье матрицы отсчетов изображения определяется в виде ряда [3.5, 3.18, 3.36, 3.45]:

1		N −1 N −1		2π i
F (u, v) =	N	·	X(j, k) · exp[−	N	(uj + vk)],	(7.7)
		j=0 k=0

а обратное преобразование имеет вид:

1		N −1 N −1		2π i
X(j, k) =	N	·	F (u, v) · exp[	N	(uj + vk)].	(7.8)
		u=0 v=0

По аналогии с терминологией непрерывного преобразования Фурье переменные u и v называют пространственными частотами. Поскольку ядра преобразования симметричны и разделимы, двумерное преобразование можно выполнить в виде последовательных одномерных преобразований по строкам и столбцам матрицы изображения.

Базисными функциями преобразования являются экспоненты с комплексными показателями, которые можно разложить на косинусную и синусную составляющие:

1

2π i

AR(n, m) = AC (n, m) = tn =

√

exp(−

nm) =

N

N

1

2π

i

2π

=

√

cos

nm −

√

sin

nm;

(7.9)

N

N

N

N

B

(n, m) = B

(n, m) = t

=

1

exp(

2π i

nm) =

R

C

n

√

N

N

1

2π

i

2π

=

√

cos

nm +

√

sin

nm;

(7.10)

N

N

N

N

0 n, m N − 1.

7.1. Дискретные линейные ортогональные преобразования

Рис. 7.1. Одномерные базисные функции преобразования Фурье при N = 16

На рис. 7.1 слева и в центре приведены графики соответственно синусных и косинусных составляющих одномерных базисных функций преобразования Фурье для N = 16.

Из этого рисунка видно, что для низких частот эти функции являются грубыми аппроксимациями непрерывных синусоид. С повышением частоты сходство базисных функций с синусоидами теряется. Для наивысшей частоты базисная функция представляет собой меандр.

Можно заметить избыточность наборов синусных и косинусных составляющих: при преобразовании N чисел X1, . . . , XN формируется N комплексных

коэффициентов

1 N −1

2π i

P (u) =

√

N n=0

Xn exp(−

N

nu) =

1

N −1

2π

i

N −1

2π i

√

nu −

√

nu; (7.11)

=

Xn cos

N

Xn sin

N

N n=0

N n=0

0 u N , состоящих из N действительных и N мнимых чисел.

При этом очевидно, что P (1 + m) = P (N − m − 1), 0 m N − 2. По этой причине обычно используется так называемое действительное дискретное Фурье преобразование (ДДПФ), базисные функции которого с учетом нормирующего множителя определяются, например, следующим образом [3.17]:

Глава 7. Групповое кодирование изображений

tR0 = t0;

. . . . . . . . . . . . . . . . . . . . .

R		√
t2n−1	= 2Retn;
R	√								(7.12)
		2Imtn;
t2n =
. . . . . . . . . . . . . . . . . . . . .
							,		N = 2M.
tNR =	t 2							2
					2Imt				, N = 2M − 1,
		√						N −1
			N

Эти базисные функции приведены на рис. 7.1. справа.

Возможен и другой вариант реализации ДДПФ. Например, для четного N

рассчитываются значения новых дискретных отсчетов:

X N

j + X N +j

N

g1 (j) =

2 −

2

,

j = 0, . . . ,

− 1;

2

2

−X N2 −j + X N2

+j

N

g2 (j) =

2

,

j = 0, . . . ,

2

− 1.

и формируется N также действительных коэффициентов:

N2 −1

N

2

2π

u = 0, . . . ,

;

Pcos(u) = +N

j=0

g1(j) cos

N ju,

2

N2 −1

2π

N

2

u = 0, . . . ,

,

Psin(u) = +N

j=0

g2(j) sin

N ju,

2

характеризующих величину и фазу соответствующих спектральных компонентов сигнала

mod P (0)

= Pcos(0),

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

mod P (u) =

,

Pcos2 (u) + Psin2 (u)

arg P (u) = Arctg

Psin(u)

, u = 1, . . . ,

N

− 1,

(7.13)

Pcos(u)

2

. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

mod P (

N

N

N

) = Pcos(

),

arg P (

) = 0.

2

2

2

Величины спектральных компонент сигнала P (u), как правило, с ростом частоты u/N падают. Это приводит к уплотнению энергии в коэффициентах с меньшими частотными индексами.

Действительное дискретное преобразование Фурье удобно для применения в связи с возможностью реализации быстрых алгоритмов расчета (так называемое быстрое преобразование Фурье — БПФ). Если для реализации ДПФ требуется выполнение примерно N 2 комплексных умножений и сложений, то при БПФ необходимо обеспечить N · log2 N таких операций [3.46–3.50].

7.1. Дискретные линейные ортогональные преобразования

Сокращение визуальной избыточности информации при использовании унитарных преобразований, в том числе преобразования Фурье, связано с осуществлением различных видов квантования полученных спектральных компонент [3.17]. Наиболее простой вариант квантования связан с формированием кодов

Q (u) = round[Q(u)/KQ],

(7.14)

где обозначение Q(u) характеризует действительные и мнимые части коэффициентов Фурье-преобразования Pcos(u) и Psin(u), либо их модуль mod (P (u)) и фазу arg(P (u)); KQ — некоторые числа (обычно кратные 2), зависящие только от вида информации Q.

При восстановлении изображения определение коэффициентов, по которым производится расчет уровней соответствующих пикселов, осуществляется по формуле

ˆ	(7.15)
Q(u) = Q · KQ.

Увеличение коэффициента KQ приводит к увеличению коэффициента сжатия изображения и к увеличению погрешностей восстановления пикселов.

Таким образом, степень сжатия и погрешность преобразования являются функцией коэффициента KQ: при уменьшении этого коэффициента уменьшается погрешность преобразования, но падает степень сжатия. Для каждого унитарного преобразования существуют свои оптимальные значения KQ.

Исследования сокращения избыточности изображений с использованием Фу- рье-преобразования показали его недостаточную эффективность.

В то же время известное свойство инвариантности модуля спектра Фурье относительно сдвига входного сигнала при простом преобразовании фазового спектра — смещении на некоторую величину, линейно зависящую от частоты спектральных компонент, позволяет надеяться на возможность использования ДПФ при анализе изображений, содержащих элементы, подобные друг другу с точностью до сдвига.

Эта возможность представляет собой альтернативу распространенным методам поиска величины сдвига, основанным на итерационной минимизации суммы модулей (или квадратов) разностей соответствующих величин в двух блоках.

7.1.2. Преобразование Хаара

Преобразование Хаара основывается на использовании ортогональной матрицы Хаара [3.17, 3.18, 3.38, 3.39, 3.51]. В табл. 7.1 приведены примеры ортогональных матриц Хаара четвертого, восьмого и шестнадцатого порядков. Преобразование Хаара можно рассматривать как процесс дискретизации исходного сигнала, при котором с переходом к следующей строке вдвое уменьшается шаг дискретизации.

Хааровский спектр описывает распределение энергии компонент, соответствующих разностям яркостей соседних пикселов, разностям средних значений яркостей соседних пар пикселов и вообще разностям средних значений яркостей соседних групп из 2m элементов.

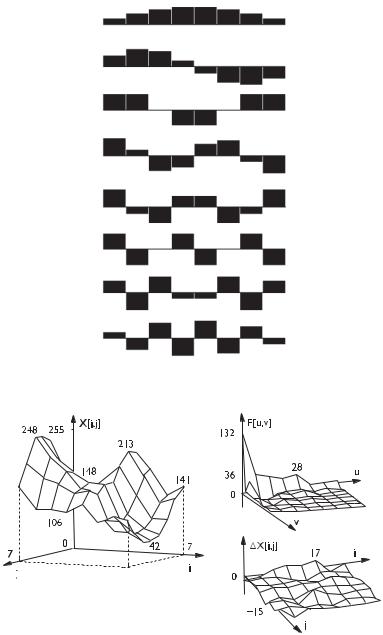
На рис. 7.2 приведены псевдотрехмерные матрицы блока изображения с числом пикселов 8 × 8 (слева), хааровского спектра (с округлением коэффициентов) и ошибок восстановления значений пикселов исходного блока изображения (справа внизу).

Глава 7. Групповое кодирование изображений

Отметим, что в спектре Хаара наблюдается концентрация энергии в областях низких хааровских частот.

7.1.3. Преобразование Уолша–Адамара

Преобразование Уолша–Адамара можно рассматривать как дискретный аналог непрерывного преобразования по базису, составленному из функций Уолша [3.5, 3.17, 3.18, 3.36, 3.37, 3.52–3.54]. Оно основано на квадратной матрице, элементы которой равны плюс или минус единице, а строки и столбцы образуют ортогональные векторы.

Среди ортогональных матриц Уолша–Адамара наименьшей является матрица второго порядка N = 2:

7.1. Дискретные линейные ортогональные преобразования

Рис. 7.2. Блок изображения 8 × 8 пикселов и его преобразование Хаара

H2 = √2			1	−	1	.
1			1
				1
n
Наиболее просто удается построить		матрицы				Уолша–Адамара, если они име-

ют порядок N = 2 , где n — целое число.

Если HN — матрица Уолша–Адамара N -го порядка, то
										H2N = √2							HN	−		HN	..
														1			HN
Например, число изменений знака
H		=	1 H2					H2			=	1		1			1	1		1		− − − − − − − − −3
	4					H H								1		−1		1		−1		− − − − − − − − −1
														1			1	1		1		0
			√2			2	−		2			2		1			1	−1		−1		− − − − − − − − −2
																− −						− − − − − − − − −
Строки матрицы H2N можно рассматривать как																						последовательность отсче-

тов прямоугольных периодических колебаний (сигналов), период которых кратен 1/N . Следовательно, матрица Уолша–Адамара описывает преобразование, связанное с разложением блоков изображений по семейству прямоугольных базисных функций, а не по синусам и косинусам, характерным для преобразований Фурье.

Обычно матрицу Уолша–Адамара упорядочивают путем перестановок строк

в порядке возрастания числа изменений знака.
Например, упорядоченная матрица 4-го порядка имеет вид:
У			1		1 −1		1			− − − − − − − − −2
			1	1		1	1				0
						−				− − − − − − − − −3
	2		1					1
число изменений знака H4 = 1				−1 1			−
			1	−		1				− − − − − − − − −
				1			−1			− − − − − − − − −1
										n
Для упорядоченной матрицы Адамара						порядка N =				2 двумерное преобразо-

вание можно представить в виде

Глава 7. Групповое кодирование изображений

Рис. 7.3. Базисные функции упорядоченного преобразования Уолша–Адамара при N = 8

1		N −1 N −1
F (u, v) =	N	X(j, k) · (−1)q(j,k,u,v),	(7.16)
		j=0 k=0

n!−1

где q(j, k, u, v) = [gi(u) · ji + gi(v) · ki], причем

i=0

g0(u) = un−1;

g1(u) = un−1 + un−2 g2(u) = un−2 + un−3

.. . . . . . . . . . . . . . . . . . . .

gn−1(u) = u1 + u0;

;

;

. . . . . . . .

ui, vi, ji, ki — цифры в двоичном представлении чисел u, v, j, k соответственно. Например, если

u = 13 = 1 · 20 + 0 · 21 + 1 · 22 + 1 · 23,

то

u0 = 1; u1 = 0; u2 = 1; u3 = 1.

На рис. 7.3 приведено изображение базисных функций упорядоченного преобразования Уолша–Адамара при N = 8.

На рис. 7.4 приведены псевдотрехмерные матрицы блока изображения, аналогичного рис. 7.2, спектра Уолша–Адамара (с округлением коэффициентов) и ошибок восстановления значений пикселов исходного блока изображения.

Отметим, что, как и в преобразовании Хаара, здесь наблюдается концентрация энергии в областях низких частот. Эффективность использования преобразования Уолша–Адамара для сжатия изображений практически такая же, как эффективность применения преобразования Хаара.

7.1. Дискретные линейные ортогональные преобразования

Рис. 7.4. Блок изображения 8 × 8 пикселов и его преобразование Уолша–Адамара

7.1.4. Дискретное синусное преобразование

Двумерное синусное преобразование определяется соотношением [3.18, 3.55]:

2		N −1 N −1		π(j + 1)(u + 1)
							×
F (u, v) =	N + 1	j=0 k=0 X(j, k) · sin		N + 1
		× sin	π(k + 1)(v + 1)		,		u, v = 0, . . . , N − 1. (7.17)
				N + 1

Обратное преобразование имеет такой же вид. Графики базисных функций синусного преобразования для N = 8 приведены на рис. 7.5.

На рис. 7.6. показаны три псевдотрехмерные матрицы: блока изображения, аналогичного рис. 7.4, спектра синусного преобразования и ошибок восстановления значений пикселов исходного блока.

Концентрация энергии в областях низких частот синусного преобразования также очевидна. Ошибка восстановления в данном случае меньше, чем при использовании преобразований Уолша–Адамара и Хаара, что говорит о большей эффективности синусного преобразования.

7.1.5. Дискретные косинусные преобразования

Известно, что ряд Фурье для любой непрерывной действительной и симметричной (четной) функции содержит только действительные коэффициенты, соответствующие косинусным членам ряда. В соответствующей интерпретации этот результат можно распространить и на дискретное преобразование Фурье изображений.

Имеется несколько способов преобразования блоков изображений с целью создания симметричных дискретных функциональных соотношений [3.18, 3.56].

Один из них заключается в том, что к изображению вплотную пристраивают его зеркальное отражение, как показано на рис. 7.7 слева.

Второй способ заключается в том, что оригинал и отражения пристраиваются, посредством наложения крайних элементов (рис. 7.7, справа).

Глава 7. Групповое кодирование изображений

Рис. 7.5. Базисные функции синусного преобразования при N = 8

Рис. 7.6. Блок изображения 8 × 8 пикселов и его синусное преобразование

Таким образом, из первоначального массива, содержащего N × N пикселов, в первом случае, называемом четным косинусным преобразованием, получают массив 2N × 2N элементов, а во втором случае — нечетном косинусном преобразовании — массив (2N − 1) × (2N − 1) элементов.

7.1. Дискретные линейные ортогональные преобразования

Рис. 7.7. Способы обработки блоков изображения при создании косинусных преобразований

Вычисление двумерного преобразования Фурье при использовании наложения крайних элементов блока приводит к нечетному косинусному преобразованию, определяемому соотношениями:

1

N −1 N −1

˜

F (u, v) =

X(j, k), u, v = 0;

(7.18)

N

j=0 k=0

2

N −1 N −1 ˜

2πju

2πkv

−

1 · cos

2N

−

1

, u, v = 0,

(7.19)

F (u, v) = N j=0 k=0 X(j, k) · cos 2N

где значения ˜ связаны со значениями пикселов исходного изображения так:

X(j, k)

1 X(j, k) при j = 0, k = 0;

4

˜	1	при j = 0, k = 0 или j = 0, k = 0;	(7.20)
X(j, k) =	2 X(j, k)
	X(j, k)	при j = 0, k = 0.

Обратное преобразование вычисляется аналогичным образом:

˜

1

N −1 N −1

X(j, k) =

F (u, v), j, k = 0;

(7.21)

N

u=0 v=0

˜

2

N −1 N −1

2πju

2πkv

−

1 · cos

2N

−

1

, j, k = 0;

(7.22)

X(j, k) = N u=0 v=0 F (u, v) · cos 2N

X(j, k) =

2X˜ (j, k),

при j = 0, k = 0 или j = 0, k = 0;

(7.23)

˜

при j = 0, k = 0;

4X(j, k),

X˜ (j, k),

при j = 0, k = 0.

Базисные функции нечетного косинусного преобразования являются, как следует из приведенных выше соотношений, разделимыми, так что двумерное нечетное косинусное преобразование можно осуществлять с использованием одномерных операций, выполняемых последовательно.