
Отношения
.docxТема: Отношения
Цель работы:
-
Изучить основные понятия бинарных отношений;
-
Изучить задание отношений и их свойства.
Задание
На множестве Х: {х1, х2, x3, x4} = {1, 2, 3, 4} заданы отношения:
а) R = «<»; б) R = «>»; в) R = «≥»; г) R = «=»; д) R = «≠».
Для каждого отношения R определить его как подмножество декартова произведения Х × X, построить матрицу отношения С, определить свойства отношения.
Для каждого свойства выписать формулу, нарисовать граф, привести пример.
а) R = «<»
Х × X = {х1, х2, x3, x4} × {х1, х2, x3, x4} = {х1x1, х1x2, х1x3, х1x4, х2x1, х2x2, х2x3, х2x4, х3x1, х3x2, х3x3, х3x4, х4x1, х4x2, х4x3, х4x4} = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)}.
R = {х1x2, х1x3, х1x4, х2x3, х2x4, х3x4} = {(1,2), (1,3), (1,4), (2,3), (2,4), (3,4)}.
|
C |
1 |
2 |
3 |
4 |
|
1 |
0 |
1 |
1 |
1 |
|
2 |
0 |
0 |
1 |
1 |
|
3 |
0 |
0 |
0 |
1 |
|
4 |
0 |
0 |
0 |
0 |
Свойства отношения:
-
Транзитивность xRy и yRz => xRz x = 1 y = 2 z = 3 1 < 2 2 < 3 => 1 < 3

б) R = «>»
Х × X = {х1, х2, x3, x4} × {х1, х2, x3, x4} = {х1x1, х1x2, х1x3, х1x4, х2x1, х2x2, х2x3, х2x4, х3x1, х3x2, х3x3, х3x4, х4x1, х4x2, х4x3, х4x4} = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)}.
R = {х2x1, х3x1, х3x2, х4x1, х4x2, х4x3} = {(2,1), (3,1), (3,2), (4,1), (4,2), (4,3)}.
|
C |
1 |
2 |
3 |
4 |
|
1 |
0 |
0 |
0 |
0 |
|
2 |
1 |
0 |
0 |
0 |
|
3 |
1 |
1 |
0 |
0 |
|
4 |
1 |
1 |
1 |
0 |
Свойства отношения:
-
Транзитивность xRy и yRz => xRz x = 4 y = 3 z = 3 4 > 3 3 > 2 => 4 > 2

в) R = «≥»
Х × X = {х1, х2, x3, x4} × {х1, х2, x3, x4} = {х1x1, х1x2, х1x3, х1x4, х2x1, х2x2, х2x3, х2x4, х3x1, х3x2, х3x3, х3x4, х4x1, х4x2, х4x3, х4x4} = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)}.
R = {х1x1, х2x1, х2x2, х3x1, х3x2, х3x3, х4x1, х4x2, х4x3, х4x4} = {(1,1), (2,1), (2,2), (3,1), (3,2), (3,3), (4,1), (4,2), (4,3), (4,4)}.
|
C |
1 |
2 |
3 |
4 |
|
1 |
1 |
0 |
0 |
0 |
|
2 |
1 |
1 |
0 |
0 |
|
3 |
1 |
1 |
1 |
0 |
|
4 |
1 |
1 |
1 |
1 |
Свойства
отношения:
-
Рефлексивность xRx x = 1 => 1 ≥ 1
-
Транзитивность xRy и yRz => xRz x = 4 y = 3 z = 3 4 > 3 3 > 2 => 4 > 2

г) R = «=»
Х × X = {х1, х2, x3, x4} × {х1, х2, x3, x4} = {х1x1, х1x2, х1x3, х1x4, х2x1, х2x2, х2x3, х2x4, х3x1, х3x2, х3x3, х3x4, х4x1, х4x2, х4x3, х4x4} = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)}.
R = {х1x1, х2x2, х3x3, х4x4} = {(1,1), (2,2), (3,3), (4,4)}.
|
C |
1 |
2 |
3 |
4 |
|
1 |
1 |
0 |
0 |
0 |
|
2 |
0 |
1 |
0 |
0 |
|
3 |
0 |
0 |
1 |
0 |
|
4 |
0 |
0 |
0 |
1 |
Свойства
отношения:
-
Рефлексивность xRx x = 1 => 1 = 1
-
Транзитивность xRy и yRz => xRz x = 1 y = 1 z = 1 1 = 1 1 = 1 => 1 = 1

-
Симметричность xRy => yRx 1 = 1 => 1 = 1

д) R = «≠»
Х × X = {х1, х2, x3, x4} × {х1, х2, x3, x4} = {х1x1, х1x2, х1x3, х1x4, х2x1, х2x2, х2x3, х2x4, х3x1, х3x2, х3x3, х3x4, х4x1, х4x2, х4x3, х4x4} = {(1,1), (1,2), (1,3), (1,4), (2,1), (2,2), (2,3), (2,4), (3,1), (3,2), (3,3), (3,4), (4,1), (4,2), (4,3), (4,4)}.
R = {х1x2, х1x3, х1x4, х2x1, х2x3, х2x4, х3x1, х3x2, х3x4, х4x1, х4x2, х4x3} = {(1,2), (1,3), (1,4), (2,1), (2,3), (2,4), (3,1), (3,2), (3,4), (4,1), (4,2), (4,3)}.
|
C |
1 |
2 |
3 |
4 |
|
1 |
0 |
1 |
1 |
1 |
|
2 |
1 |
0 |
1 |
1 |
|
3 |
1 |
1 |
0 |
1 |
|
4 |
1 |
1 |
1 |
0 |
Свойства отношения:
-
Симметричность xRy => yRx 1 ≠ 2 => 2 ≠ 1

Контрольные вопросы:
Определение бинарного отношения.
Соответствием между множествами X и Y (или соответствием из X в Y) называется любое подмножество декартова произведения X × Y. Если множества X и Y совпадают, то соответствие между множествами X и Y называют также бинарным отношением на множестве X.
Декартовым
произведением множеств X и Y называется
множество X × Y всех упорядоченных
пар (x, y) таких, что x![]() X, y
X, y![]() Y.
Y.
Свойства отношений и их интерпретация с помощью теории графов.
Бинарное отношение R на
множестве X называется рефлексивным,
если для любого элемента a![]() X выполняется
условие a R a:
X выполняется
условие a R a:
(![]() a
a![]() X) a
R a
X) a
R a
Если отношение представлено с помощью графа, то рефлексивность этого отношения означает, что в каждой вершине графа обязательно имеется петля.
Для отношения, заданного с помощью булевой матрицы его рефлексивность равносильна тому, что по главной диагонали этой матрицы (идущей из ее левого верхнего угла в правый нижний) стоят только символы 1.
Бинарное отношение R на множестве X называется симметричным, если из a R b следует b R a:
(![]() a, b
a, b![]() X)(a
R b
X)(a
R b![]() b
R
a)
b
R
a)
В графе симметричного отношения для каждой дуги из вершины x в вершину y имеется дуга из y в x. Матрица симметричного отношения симметрична относительно главной диагонали.
Объединение и пересечение любого семейства симметричных отношений снова являются симметричными отношениями.
Бинарное отношение R на
множестве X называется транзитивным,
если для любых трех
элементов a, b, c ![]() X из aRb и bRc следует aRc:
X из aRb и bRc следует aRc:
(![]() a, b, c
a, b, c ![]() X)
(aRb & bRc
X)
(aRb & bRc ![]() aRc).
aRc).
Определение отношения эквивалентности.
Бинарное отношение называется отношением эквивалентности, если отвечает условиям:
-
Рефлексивность:
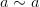 ,
, 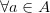 ;
; -
Симметричность:
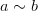 ,
то
,
то 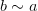 ,
, 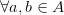 ;
; -
Транзитивность:
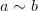 и
и 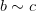 ,
то
,
то 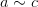 ,
, 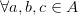 .
.
Если ![]() связан
с
связан
с ![]() ,
будем писать
,
будем писать ![]() и
говорить, что
и
говорить, что ![]() эквивалентен
эквивалентен ![]() .
.
Определение отношения порядка.
Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество. Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе, как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия:
-
Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности.
-
Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).
Множества обычно обозначаются заглавными
латинскими буквами. Если элемент ![]() принадлежит
множеству
принадлежит
множеству ![]() ,
то это обозначается:
,
то это обозначается:
![]()
Если каждый элемент множества ![]() является
также и элементом множества
является
также и элементом множества ![]() ,
то говорят, что
множество
,
то говорят, что
множество ![]() является подмножеством множества
является подмножеством множества ![]() :
:
![]()
Подмножество ![]() множества
множества ![]() называется собственным
подмножеством, если
называется собственным
подмножеством, если
![]()
Используя понятие множества можно построить более сложные и содержательные объекты.
