56

Глава 2.

2.4Точные решения

Несмотря на простой вид, стохастические уравнения (2.4) аналити- чески интегрировать не так и просто из-за винеровского члена W . Это

явно видно в случае конечной численной реализации (2.5). Каждое последовательное x в итерационной процедуре нелинейным образом зависит

от всех предыдущих случайных чисел "k (l C19). Тем не менее, рассмот- рим ситуации, в которых можно получить точные решения.

Пусть в процессе Ито функции сноса и волатильности зависят только от времени. Обозначим их через f(t) и s(t):

dx = f(t) dt + s(t) W:

(2.17)

Это уравнение легко интегрируется при помощи дискретной интерпретации стохастического члена W . Рассмотрим итерации, выполняемые

по разностной схеме (2.5):

p	p
x1 = x0 + f0 t + s0"1p t;

x2 = x1 + f1 t + s1"2 t = x0 + (f0 + f1) t + (s0"1 + s1"2) t;

:::;

ãäå fk = f(tk) è sk = s(tk). После n итераций итоговое значение будет

равно:

p

x = x0 + (f0 + ::: + fn 1) t + (s0"1 + ::: + sn 1"n) t:

Скобки в последнем слагаемом содержат сумму независимых гауссовых чисел, каждое из которых имеет волатильность sk. В результате получа-

ется гауссово число с волатильностью		s2 + ::: + s2
дя к непрерывному пределу, получаем q(l0H9):				n 1. Поэтому, перехо-
Zt		2Zt		31=2
x(t) = x(t0) + t0	f( ) d + 4t0		s2( ) d 5		":	(2.18)

Решение (2.18) уравнения (2.17) говорит нам, что x(t) является нор-

мально распредел¼нным случайным числом со средним и дисперсией,

зависящими от времени. Если s(t) не константа, то будущая неопреде- p

л¼нность в значении x может увеличиваться уже не как t, а по другому

закону.

Соотношение (2.18) позволяет легко âычислить статистические свойства процесса, в частности, его среднее x(t) и волатильность (t).

Стохастические уравнения

57

Одномерное уравнение Ито для процесса, имеющего произвольный снос a(x; t) и волатильность b(x; t)

dx = a(x; t) dt + b(x; t) W;

(2.19)

заменой иногда можно свести к частному случаю (2.17), для которого решение уже известно. Воспользуемся леммой Ито:

dF =

@F

@F

b2

x; t

)

@2F

dt + b(x; t)

@F

+ a(x; t)

+

(

W: (2.20)

@t

@x

2

@x2

@x

|

}

|

f(t)

s{z(t)

{z

}

Подберем F (x; t) таким образом, чтобы множители при W и dt в (2.20) оказались функциями s(t) и f(t), зависящими только от времени:

@x	= b(x; t);		@t	+ s(t)	b(x; t)	2 @x		= f(t); (2.21)
@F		s(t)	@F		a(x; t)	1 @b(x; t)

где вместо @F=@x в множитель при dt подставлено первое уравнение (2.21) и его производная по x (l H10). Возьм¼м частные производные первого уравнения (2.21) по t и второго по x. Вычитая их, мы прид¼м к

условию совместности:

1 @

s(t)

1 @2b(x; t)

@

a(x; t)

=

:

(2.22)

s(t) @t

b(x; t)

2 @x2

@x

b(x; t)

Если при данных a(x; t) и b(x; t) можно подобрать такую функцию s(t),

при которой уравнение (2.22) обратится в тождество, то мы получим решение стохастического уравнения (2.19) в следующей неявной форме:

	t		2	Z	t	31=2
F x(t); t = F	Z
	x(t0); t0 + t0	f( ) d +	4	t0	s2( ) d	5	";	(2.23)
где функция f(t)								F (x; t)
	определяется вторым соотношением (2.21), à

находится из первого уравнения (2.21) ( l C20).

Решение (2.23) это нестационарный гауссовый процесс для деформации x(t) при помощи нелинейной функции F (x; t). Естественно, что

разрешимость (2.22) позволяет интегрировать уравнение Ито только в ряде частных случаев. Однако, как мы увидим ниже, эти случаи охватывают достаточно широкий класс важных для практических приложений процессов.

58

Глава 2.

2.5Простые стохастические модели

Логарифмическое блуждание определяется уравнением:

dx = x dt + x W	;	(2.24)

где и константы модели. Часто (2.24) называют геометрическим

или экспоненциальным броуновским блужданием.

Если стохастического члена нет ( = 0), то это обычное уравнение экспоненциального роста ( > 0) или снижения ( < 0):

dx	= x	=>	x(t) = x0 e t:
dt

Подобная зависимость возникает во многих физических, биологических и социальных системах, от радиоактивного распада до роста экономики.

Случайное воздействие вносит в гладкую динамику определ¼нные коррективы. Подставим функции сноса a(x; t) = x и волатильности b(x; t) =

x в условие совместности (2.22) íà ñòð. 57. В результате для s(t) получается тривиальное уравнение s(t) = 0, где точка сверху обозначает производную по времени. Следовательно, s(t) это константа, которую удобно выбрать равной . Интегрирование первого уравнения (2.21) да¼т F (x; t) = ln x, и, соответственно, функция f(t) равна 2=2. Оконча- тельное решение (t0 = 0) имеет вид:

p

x(t) = x0 e( 2=2)t+ t ": (2.25)

Если в процессе Винера x может уползти при блуждании в область отрицательных значений x < 0, то для логарифмической модели это невоз-

можно. Подобное свойство можно было ожидать сразу по виду (2.24). По мере приближения к значению x = 0 снос и волатильность уменьшаются.

В результате динамика как бы замораживается при x ! 0.

Используя интеграл (1.11) íà ñòð. 16, легко вычислить среднее значе- ние и волатильность в произвольный момент времени:

p

x(t) = x0 e t; x(t) = x(t) e 2t 1:

Заметим, что необходимо решительно бороться с искушением по обыч- ному обращаться со стохастическими уравнениями. Например, разделив (2.24) на x, нельзя внести его под дифференциал: dx=x 6= d ln x. Для

подобных действий служит лемма Ито (2.15) по которой для процесса логарифмического блуждания d(ln x) = ( 2=2) dt + W . Фактиче-

ски, при помощи этой замены, найденной по алгоритму стр. 57, мы и получили решение (2.25).

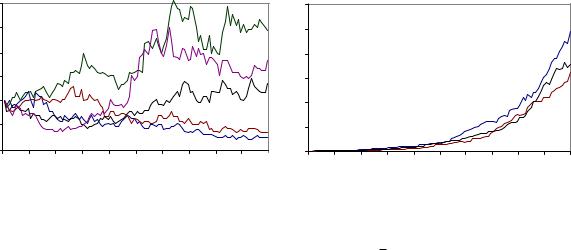
Стохастические уравнения

59

Ниже на левом рисунке приведены логарифмические блуждания с нулевым сносом: dx = x W . Видно, как они, прижимаясь к x = 0, тем

не менее, остаются в положительной области. В результате получается несимметричное распределение для x, которое в данном случае имеет

логнормальный вид. Справа динамика дополнена детерминированным сносом: dx = 0:05 x (dt + W ). Она имеет ярко выраженный экспонен-

циальный рост со стохастическими колебаниями вокруг экспоненты.

3
	500
2	400
	300
1	200
	100
0	0

Эти два примера напоминают нам, что стохастические процессы могут быть как малыми поправками к детерминированной динамике (справа),

так и основной сутью исследуемой системы (слева). p

Введя винеровский процесс Wt = W (t) = " t, решение для логарифмического блуждания можно записать в следующем виде:

x(t) = e( 2=2)t+ Wt:

Действительно, производные для x(t) = F (t; W ) равны:

@x	= ( 2=2) x;	@x	= x;	@2x	= 2 x:
@t		@W		@W 2

Винеровское блуждание Wt имеет нулевой снос a = 0 и единичную волатильность b = 1. Поэтому по лемме Ито (2.15) имеем:

dx =	@x	+	1 @2x			dt +	@x	W = x dt + x W:
	@t		2 @W 2				@W

Роль x теперь играет процесс W , а функция F это x.

Задавая различные функции x = F (t; Wt), удовлетворяющие начальному условию x0 = F (0; 0), можно найти целый класс точно решаемых стохастических уравнений. После подстановки F (t; Wt) в лемму Ито необходимо исключить Wt, заменив е¼ на Wt = G(t; x), где G обратная к F функция. Кроме этого константа x0 должна сократиться, так как этовнешнее к динамике условие и порядочное уравнение не должно зависеть от него. В качестве упражнения стоит проверить решения ( R38)(R43) из Справочника (стр. 276). К сожалению, чаще таким методом получаются уравнения, в которых снос зависит от волатильности шума, что не очень естественно для практических приложений.

60

Глава 2.

Процесс Орнштейна - Уленбека:

dx = (x ) dt + W

(2.26)

описывает блуждание, в котором x притягивается к уровню, определяемому константой . При этом волатильность считается постоянной. Если x , то снос становится заметно отрицательным и тянет процесс вниз. При опускании x ниже снос оказывается положительным и в среднем поднимает x(t) вверх. Параметр > 0 характеризует величинусилы притяжения к равновесному значению .

Условие совместности (2.22) да¼т уравнение s(t) = s(t). Решая его и первое уравнение (2.21) для F (x; t), мы каждый раз выбираем константы

интегрирования наиболее удобным способом , так как начальные условия уже учтены в (2.23), а нам необходимо найти простейшую замену, исключающую x из сноса и волатильности:

s(t) = et;

F (x; t) = xet;

f(t) = et:

В результате решение записывается в следующем виде ( t0 = 0):

	e 2t ":
x(t) = + x0 e t + p2 p1		(2.27)

Несложно увидеть, что x(t) оказывается гауссово распредел¼нной вели- чиной со средним и дисперсией, зависящими от времени.

Если > 0, то среднее при больших временах стремится к равновес- p

ному уровню . Волатильность становится равной = 2 . При винеровском или логарифмическом блуждании x(t) может уйти как угодно далеко от своего начального значения x0. Для процесса (2.26) x(t) заперта

âñòàòèстическом коридоре с шириной, равной двойной волатильности p

= 2 .

При малых процесс Орнштейна-Уленбека по своему поведению ста-

новится очень близким к обычному винеровскому блужданию. Траекто-

рия x(t) достаточно долго блуждает выше или ниже , не уходя, тем p

не менее, на бесконечность. Волатильность стремится к = 2 , и тем больше, чем меньше . Следовательно, характерный коридор, в котором происходит блуждание, при малых расширяется. Если и , и достаточно большие, x(t) часто пересекает равновесный уровень, начиная напоминать обычный белый шум.

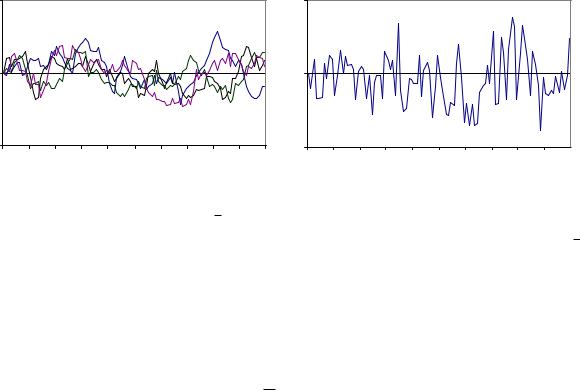
Стохастические уравнения

61

Наличие равновесного уровня в модели Орнштейна-Уленбека полезно для различных финансовых приложений. Например, в случае курсов валют может быть паритетом покупательной способности ( l C21), à äëÿ процентной ставки - е¼ долгосрочным значением.

Примеры реализаций блуждания Орнштейна-Уленбека при различ- ных параметрах приведены ниже. На левом рисунке = 0:1, = 0:1.

На правом = 1, = 0:5. Величина в обоих случаях равна единице.

2

1

0

2

1

0

Необходимо помнить, что, если решение выражено через винеровскую

переменную Wt, е¼ всегда pможно переписать через гауссову случайную

величину, заменив Wt = " t. Обратное, вообще говоря, не верно. Если p

в решении есть ", нельзя его выразить через Wt, подставив " ! Wt= t. В качестве упражнения имеет смысл проверить, что подобная замена в (2:27) приводит к случайной функции, не удовлетворяющей (2.26).

Можно объединить положительность x и его притяжение к равновесному уровню в следующей логарифмической модели с притяжением:

dx = x ln	x	1 dt + x W:	(2.28)

Если x > , то снос отрицательный, а при x < положительный. Множитель x замораживает динамику при приближении к x = 0. Для

этой модели несложно найти точное решение ( l H11).

На самом деле логарифмическая модель с притяжением является про-

стой деформацией процесса Орнштейна-Уленбека. Действительно, если x удовлетворяет уравнению (2.26), то несложно проверить, что y = ex

будет удовлетворять (2.28). Уравнение (2.28) так же соотносится с (2.26), как логарифмическое блуждание с процессом Винера.

Ещ¼ одну модель уместно назвать броуновской ловушкой:

dx = (x ) dt + (x ) W:

(2.29)

Член со сносом обеспечивает притяжение к уровню x = , в окрестности

которого волатильность становится очень маленькой, а динамика детерминированной. В результате процесс рано или поздно гарантированно притягивается к значению x = (l H12).

62

Глава 2.

Можно рассмотреть общее стационарное уравнение, снос и волатильность которого не зависят от времени:

dx = a(x) dt + b(x) W:

Условие совместности записывается следующим образом:

s(t)	= 2 b b00	b	b 0		= ;	(2.30)
s(t)	1			a

где штрих производная по x, точка по времени, и опущены аргументы

у функций. Левая часть зависит только от времени, правая только от x, поэтому это выражение равно некоторой константе, которую мы обо-

значили через . Проинтегрировав это уравнение, найд¼м связь между сносом и волатильностью:

a =	4	0	+ b b Z	b ;
	b2			dx

где ещ¼ один параметр.

Если b(x) = = const мы приходим к уравнению ОрнштейнаУленбека (2.26), ñòð. 60. Для b(x) = x точно решаемой задачей является

логарифмическая модель с притяжением (2.28), частным ñлучаем кото- p

рой является логарифмическое блуждание. При b(x) = x снос должен явным образом зависеть от :

2

+ p

+ 2 x:

a(x) =

x

4

Решение такого уравнения имеет вид ( x0 = x(0), > 0):

px0 et + 2

et 1 + p8 p

"

2

x(t) =

e2t 1

:

Если a(x)=b(x) = const, или сноса при блуждании нет a(x) = 0, то условие совместности (2.30) упрощается:

b00 = :

2 b

Умножая его на интегрирующий множитель b0, получаем решение в неяв- ной форме:

x = Z	p + 4 ln b;
		db

где и константы интегрирования.

Стохастические уравнения											63
Броуновский мост. Рассмотрим теперь уравнение Ито со сносом,
зависящим не только от x, но и от времени t:
	dx =		x dt + W				:				(2.31)
		T t
Константа T это выделенное время в будущем ( t < T ), когда снос
становится бесконечным. Условие совместности да¼т:
				x
s(t) = T t;	F (x; t) =			T t;		f(t) =		(T t)2 :			(2.32)
В результате получаем решение в следующем виде ( x0 = x(t0)):
x(t) = + (x0 )			T	t			t	T	t	) ":
			T	t0	+ s(t T0)( t0
Среднее процесса при t ! T стремится к . При этом волатильность ока-
зывается равной нулю. Это означает, что x(t) гарантированно в процессе
блуждания достигает равновесного значения x(T ) = :
2					2.5
					2
1					1.5
					1
0					0.5
На рисунках в обоих случаях = 1. Слева = 0:1, справа = 0:05.
Соединение начального условия x0 = x(0) и конечного x(T ) = стоха-
стическими траекториями и дало живописное название процессу.
Можно рассмотреть броуновский мост в более общем случае, с произ-
вольными коэффициентами, зависящими от времени:

dx = (t) x (t) dt + (t) W:

Условия совместности дают:

t

R

s(t) = (t)et0 (t)dt; F (x; t) = x s((tt)); f(t) = (t) (t) s((tt)):

Для частного выбора (t) = =(T t), (t) = , (t) = , где ; , T иконстанты модели, получаем решение в следующем виде ( t0 = 0):

x0

(T t)

(T t)2 1

1=2

x(t) = +

(T

t) +

1

":

T

2 1

T 2 1

Заданием функции (t) можно добиться произвольного выгиба моста вверх или вниз.