Mat_analiz_ekzamen

1

Вопросы и ответы к экзамену по математическому анализу

1. Бесконечно большая величина.

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция неограниченная с обеих сторон, не является бесконечно большой при .

Последовательность называется бесконечно большой, если .

Функция называется бесконечно большой в окрестности точки , если .

Функция называется бесконечно большой на бесконечности, если либо,

.

Как и в случае бесконечно малых, необходимо отметить, что ни одно отдельно взятое значение бесконечно большой величины не может быть названо как «бесконечно большое» — бесконечно большая величина — это функция, которая лишь в процессе своего изменения может стать больше произвольно взятого числа

2.Бесконечно малая величина.

Последовательность называется бесконечно малой, если . Например,

последовательность чисел

— бесконечно малая.

Функция называется бесконечно малой в окрестности точки , .

Функция называется бесконечно малой на бесконечности, если , либо

.

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если , то , .

Подчеркнём, что бесконечно малую величину следует понимать как переменную величину

(функцию), которая лишь в процессе своего изменения *при стремлении x к a (из

)+ делается меньше произвольного числа (). Поэтому, например, утверждение типа «одна миллионная есть бесконечно малая величина» неверно: о числе *абсолютном значении+ не имеет смысла говорить, что оно бесконечно малое.

3.Свойства бесконечно малых и бесконечно больших величин , связь между ними.

Алгебраическая сумма конечного числа бесконечно малых функций есть бесконечно малая функция.

2

Произведение бесконечно малых — бесконечно малая.

Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

Если - бесконечно малая последовательность, сохраняющая знак, то бесконечно большая последовательность.

Свойства бесконечно больших.

1) Произведение бесконечно большой величины на величину, имеющую предел,

отличный от нуля, а следовательно, и произведения бесконечно большой величины

на постоянную, не равную нулю, являются величинами бесконечно большими.

2)Произведение любого определенного числа бесконечно больших величин есть также величина бесконечно большая.

3)Величина, обратная всякой бесконечно большой, есть бесконечно малая.

4)Величина, обратная бесконечно малой, будет бесконечно большой, если данная бесконечно малая в процессе своего изменения не принимает значений равных нулю.

Теорема о связи между бесконечно большой и бесконечно малой функциями:

Если функция - функция бесконечно малая (), то функция есть бесконечно большая функция и наоборот.

4.Определение предела функции в точке , его геометрический смысл.

Число A называется пределом функции y = f(x) при x → a, если для любого, даже сколь угодно малого положительного для любого, даже сколь угодно малогоε> 0, найдется такое число δ > 0 (зависящее от ε), что для всех x из δ-окрестности точки a, выполнено неравенство: | f (x) –A|<ε

Геометрический смысл

Предел функции y= f (x) в точке x → aсуществует и равен A, если для любой ε-окрестности точки A можно указать такую δ-окрестность точки a, что для любого x из этой δ-окрестности значение f (x) будет находиться в ε-окрестности точки A.

5. Свойства предела (предел константы, предел суммы двух функций, предел произведения, предел частного)

- Предел постоянной величины равен самой постоянной величине

-Предел суммы/разности двух функций равен сумме/разности их пределов

3

-Предел произведения двух функций равен произведению их пределов

-Предел частного двух функций равен частному их пределов, при условии, что предел знаменателя не равен нулю

6. Первый замечательный предел: Предел отношения синуса к его аргументу равен единице в случае, когда аргумент стремится к нулю

Таблица эквивалентности бесконечно малых:

7.Второй замечательный предел: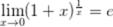

8.Сравнение бесконечно малых (три случая). Эквивалентность бесконечно малых.

Правила сравнения бесконечно малых

Пусть при функции и являются бесконечно малыми. Тогда:

1) если	, то	- бесконечно малая более высокого порядка, чем					(или, что
то же самое,	имеет более высокий порядок малости, чем					при	);
2) если		(A - число), то		и	- бесконечно малые одного порядка;
3) если	, то	и	- эквивалентные бесконечно малые. Эквивалентность
обозначается так:		.

В некоторых случаях недостаточно знать, что одна из двух бесконечно малых является бесконечно малой более высокого порядка, чем другая. Нужно ещё оценить, как высок этот порядок. Для этого существует следующее правило:

4

4) если

, то

бесконечно малая n-го порядка относительно

Б.м. функции и называются эквивалентными или равносильными б.м. одного порядка

при , если

Обозначают: при .

9.Левосторонний и правосторонний предел.

Односторонний предел — предел числовой функции, подразумевающий «приближение» к предельной точке с одной стороны. Такие пределы называют соответственно левым и правым пределами.

Число называется правым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 1).

Правый предел обозначается

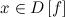Число называется левым пределом функции в точке , если для такое, что для любого и , выполняется неравенство (рис. 2). Левый предел обозначается

10.Понятие непрерывности функции:

Функция называется непрерывной в точке , если:

-функция определена в точке A и ее окрестности;

-существует конечный предел функции в точке A;

-это предел равен значению функции в точке , т.е

5

11.Классификация точек разрыва

12.Понятие производной

Производной функции в точке называется предел (если он существует и конечен) отношения приращения функции к приращению аргумента при условии, что последнее стремится к нулю.

13.Геометрический смысл производной

6

14.Таблица производных элементарных функций

15. Правила дифференцирования функции (от константы, от суммы функций, от произведения, от частного, от сложной функции)

16.Производная параметрической функции

Предположим, что функциональная зависимость от не задана непосредственно , а через промежуточную величину — . Тогда формулы

7

задают параметрическое представление функции одной переменной.

1)Пусть функция 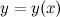задана в параметрической форме, то есть в виде:

где функции и определены и непрерывны на некотором интервале изменения параметра . Найдем дифференциалы от правых и левых частей каждого из равенств:

Далее, разделив второе уравнение на первое, и с учетом того, что , получим выражение для первой производной функции, заданной параметрически:

Для нахождения второй производной

выполним следующие преобразования:

17.Дифференцируемость функции в точке. Критерий дифференцируемости в точке.

Определения

Пусть дана функция , и —

внутренняя точка области определения f. Тогда fназывается дифференци́руемой в x0, если

существует окрестность и число

такие,что в этой окрестности для f справедливо представление

где o(x − x0) обозначает величину, пренебрежимо малую по сравнению с x − x0 при Если fдифференцируема в x0, пишут

Функция z = f(x;y) называется дифференцируемой в точке M(x;y), если ее полное приращен ие в этой точкеможно представить в виде

z = A x + B y + αΔx + βΔy,

8

где и при ,

18.Определение дифференциала функции

Линейное отображение где A —

константа из предыдущего определения, называетсядифференциа́лом функции f в точке x

0и обозначается df(x0).

19.Приращение функции

20.Дифференциал функции

Определение. Дифференциалом функции в некоторой точке x называется главная, линейная часть приращения функции.

Дифференциалом функции называется линейная относительно часть приращения функции.

Она обозначается как или . Таким образом:

21.Производные и дифференциалы высших порядков

22.Правило Лопиталя

23.Область определения функции

Область определения функции – это множество всех значений аргумента, на котором задается функция.

9

24.Теорема о связи непрерывности и дифференцируемости функции (без доказательства)

Если функция дифференцируема в точке, то она непрерывна в этой точке.

25.Определение асимптоты (типы асимптот)

Асимптота-это прямая к которой график будет приближаться, но никогда её не пересечёт.Она проходит параллельно оси у или х.Вертикальная, Наклонная и Горизонтальная (частный случай)

26.Определение вертикальной асимптоты. Схема нахождения

27.Определение наклонной асимптоты. Схема нахождения

28.Определение возрастающей на интервале функции

Функция называется возрастающей когда большему значению аргумента соответствует большее значение функции.

29.Определение убывающей на интервале функции

Функция называется убывающей когда большему значению аргумента соответствует меньшее значение функции.

30.Условие монотонности функции

(Критерий монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на и имеет в каждой точке производную Тогда

10

не убывает на тогда и только тогда, когда

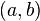не возрастает на тогда и только тогда, когда

(Достаточное условие строгой монотонности функции, имеющей производную на интервале) Пусть функция непрерывна на и имеет в каждой точке 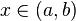производную Тогда

если то строго возрастает на

если то строго убывает на

Обратное, вообще говоря, неверно. Производная строго монотонной функции может обращаться в ноль. Однако, множество точек, где производная не равна нулю, должно быть плотно на

интервале Точнее имеет место

(Критерий строгой монотонности функции, имеющей производную на интервале) Пусть и всюду на интервале определена

производная Тогда строго возрастает на интервале тогда и только тогда, когда выполнены следующие два условия:

1.

2.

Аналогично, строго убывает на интервале тогда и только тогда, когда выполнены следующие два условия:

1.

2.

31.Максимум и минимум функции. Определение.

В точке производная меняет свой знак с плюса на минус, функция имеет максимум. В точке производная меняет свой знак с минуса на плюс, функция имеет минимум. В точке производная своего знака не меняет, экстремума там нет.

Точка называется точкой локального максимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности выполняется неравенство: .

Точка называется точкой локального минимума функции , если существует такая окрестность этой точки, что для всех из этой окрестности 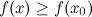.