28. Модель линейно-деформируемой среды

«Линейная» и «нелинейная» механика грунтов.

 

Приведенные выше модели грунта содержат в себе некоторое противоречие. Действительно, теория линейного деформирования грунта, справедливая в ограниченном диапазоне нагрузок, позволяет рассчитывать напряжения и деформации только при р≤р₁. Задачи, основанные на использовании этой теории, относятся к линейной механике грунтов. В то же время теория предельного равновесия позволяет устанавливать только предельные нагрузки на основание (р=р2) и не дает возможности рассчитывать соответствующие им величины осадок. Таким образом, расчет деформаций оснований в диапазоне нагрузок от р₁ до р₂ с помощью этих теорий выполнен быть не может.

Для широкого класса задач такой подход является вполне оправданным. Поэтому в следующей лекции будут рассмотрены методы определения характеристик механических свойств грунтов, необходимых для расчетов оснований с помощью этих теорий. Однако при проектировании особо ответственных сооружений оказывается целесообразным использовать и более сложные модели грунта, позволяющие определять деформации во всем диапазоне нагрузок. Эти решения относятся к нелинейной механике грунтов.

Теории нелинейного деформирования грунтов применяются для расчетов напряженно-деформированного состояния и оценки прочности оснований и грунтовых сооружений, когда связь между напряжениями и деформациями существенно нелинейна, поэтому они часто называются теориями пластичности грунтов. Сложность расчетов при этом существенно возрастает, что требует использования ЭВМ.

Значительное распространение в инженерной практике получила деформационная теория пластичности, основанная на теории малых упругопластических деформаций акад. А. А. Ильюшина. Эта теория исходит из допущения, что объемная и сдвиговая деформации зависят только соответственно от среднего нормального напряжения и интенсивности касательных напряжений, т. е. в соответствии с рис. 4.3 ε_v=f(σ_m),γ_i = Ψ(τ_i).

При этом вводятся понятия: K(σ_m) = (σ_m / ε_v — секущий модуль объемной деформации, G(τ_i)= τ_i / γ_i — секущий модуль сдвига. Поскольку графики на рис. 4.3 существенно нелинейны, величины этих модулей будут нелинейными.

При расчетах грунтовых оснований и сооружений часто можно принимать, что модуль объемной деформации зависит только от среднего нормального напряжения, тогда как модуль сдвига зависит не только от интенсивности касательного напряжения, но и от среднего нормального напряжения. Уравнения состояния в этом случае уже будут иметь значительно более сложный вид, чем обобщенный закон Гука, а именно:

 

 

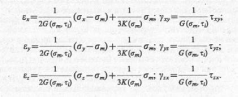
Если модули K(σ_m) могут быть определены по экспериментально полученной для данного грунта кривой на рис. 4,3, а, то для определения модулей G(σ_m, τ_i) требуется проведение экспериментов при различных значениях σ_m и τ_i. 3. Г. Тер-Мартиросян рекомендует следующее упрощенное определение модуля сдвиговой деформации:

 

G(σ_m, τ_i) =Gо(1 – η_пр)

 

где G₀ — величина модуля сдвига на начальном участке кривой на рис. 4.3, η_пр — степень приближения действующего напряженного состояния к предельному

 

 

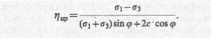
В строительной практике применяются и более сложные теории нелинейного деформирования грунтов, например теории пластического течения. Различные модификации теорий нелинейного деформирования грунтов представлены в работах С. С. Вялова, А. Л. Гольдина, Ю. К. Зарецкого, А. Л. Крыжановского, В. Г. Николаевского, В. И. Соломина, 3. Г. Тер-Мартиросяна, В. Г. Федоровского и других ученых.

Расчетная модель линейно деформируемой среды (модель среды теории упругости). В основу модели среды теории упругости положен закон Гука — линейная зависимость между напряжениями и деформациями и, что весьма существенно, представления об идеальной упругости материала — полное восстановление деформаций при снятии нагрузки, т. е. в условиях одноосного простого сжатия или растяжения (рис. 2.2, а) а = Ее, где е — осевая деформация, Е — модуль упругости. Для грунтов, наоборот, характерно наличие преимущественно остаточных деформаций. Поэтому модель среды теории упругости может применяться только на этапе однократного загружения грунтовой среды без последующей разгрузки, что для большинства практических строительных случаев статических нагрузок и происходит в действительности. Учитывая, что из закона Гука в этом случае используется только линейность зависимости между напряжениями и деформациями, Н. М. Герсеванов предложил для грунтов вместо

термина «среда теории упругости» применять более корректный в этом случае термин линейно деформируемая среда. Следует отметить, что эта рекомендация на практике не всегда выполняется и для линейно деформируемой области грунтовой среды часто в литературе и особенно докладах применяется термин «область среды теории упругости» или для удобства и сокращения «упругая» область, хотя упругость среды при этом не рассматривается. Учитывая это, в дальнейшем будем применять и ту, и другую терминологию.

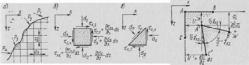
Рис. 2.3. Элементы среды (а) внутри (б) и на Рис. 2.4. Грани элемен- внешних границах (в) та до и после деформа

ций среды

 

При использовании модели линейно деформируемой среды любая -задача сводится к решению системы уравнений, в состав которой, как известно из курса теории упругости, входят статические уравнения, геометрические соотношения и физические уравнения.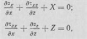

В случае плоской задачи уравнения равновесия (статические уравнения) бесконечно малого элемента (рис. 2.3, б) среды (рис. 2.3, а) имеют вид

(2.3)

где о_х, ст_г, х_хг, х_гх — нормальные и касательные напряжения по граням йх, йг элемента среды; X и 7. — составляющие объемных сил (например, собственного веса грунта).

\йх дг

Однако в большинстве задач деформации могут считаться малыми (<1), что позволяет пренебречь членами V,

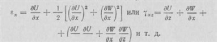
Геометрические уравнения (соотношения), связывающие линейные (е) и угловые (у) деформации со смещениями ((У, (рис. 2.4), в общем случае являются нелинейными, например: и т. д., а геометрические соотношения для плоской задачи принять в виде

ои д\у ви . д№ _т ..

г_х = — ; = — ; Тх_г = 1 • (2.4)

дх дг дг дх

Физические уравнения характеризуют зависимости между напряжениями и деформациями и принимаются в виде соотношения обобщенного закона Гука:

^Е* = (1 — ^²) ~ V (1 + V) о₂ | ;

(1 ^,'²) ^аг V (1 + V) а_х ]; ^_хг=Ш±±^_хх, (2.5)

где V — коэффициент Пуассона.

Таким образом, в общем случае для плоской задачи из восьми уравнений (2.3) — (2.5) определяются неизвестные три компоненты напряжений (сг_ж, а_г, 1_хг), три компоненты деформаций (е_х, е_г, у_хг) и две компоненты перемещений (V, №). Для условий пространственной задачи таких уравнений и неизвестных будет 15.

Помимо перечисленных имеются еще уравнения совместности (неразрывности) деформации, которые используют вместо геометрических уравнений (2.4), либо привлекают в роли контрольных соотношений проверки условия, что среда после ее нагружения остается сплошной. Иначе говоря, деформации элементарных прямоугольников, на которые до приложения нагрузки можно мысленно разделить среду (см. рис. 2.3), должны быть после приложения нагрузки совместными (см. рис. 2.4), т. е. такими, при которых не нарушается сплошность среды (не образуется щелей между гранями элементов).

Уравнения неразрывности для плоской задачи имеют вид

д²*х | д~^гг _ д² Тдгг 12 0\

дг² дх² дхдг ' '

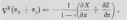
Используя физические уравнения (2.5), уравнение (2.6) может быть записано через напряжения в виде уравнения совместности Бельт- рами—Митчеля:

д^г д²

где у² — оператор Лапласа у² 1 .

дх² дг²

Само решение задачи теории упругости производится тремя основными методами: напряжений (сил), перемещений и смешанным. В частности, при решении плоской задачи методом сил система уравнений линейно деформируемого тела состоит из двух уравнений равновесия (2.3) и уравнения совместности (2.7) с тремя неизвестными (ст*,

<^2> Т-жг)-

Помимо уравнений равновесия и совместности напряжения и перемещения среды должны удовлетворять соответствующим для каждого частного случая граничным условиям, т. е. принимать на границе среды

_ д*<р , _п .

(2-8)

заданные значения (см, рис. 2.3, а). Уравнения, связывающие заданные граничные напряжения (а_р, х_р) с напряжениями внутри среды, получаются для плоской задачи из рассмотрения условий равновесия граничного треугольного элемента среды (см. рис. 2.3, в) и приводятся в курсах теории упругости.

При решении системы уравнений модели среды теории упругости

и (2.7) эффективно введение потенциальной функции (^/ф) и функции напряжений (ср), удовлетворяющих условиям равновесия (2.3).

В этом случае составляющие объемных сил могут быть представлены в виде

_{х =} _ дЦф_ _и 2 ₌ _^Ф₎ дх дг

а напряжения выражены через ф и И_ф как

которое и подвергается интегрированию при решении конкретных задач теории линейно деформируемого тела.

В заключение необходимо подчеркнуть, что модель среды теории упругости, учитывая естественные условия равновесия и неразрыв- ности (сплошности) среды, предполагает, что при любом напряженном состоянии соблюдается закон Гука, т. е. линейная зависимость между напряжениями и деформациями и не в одной точке грунтовой среды ни при каких условиях не может возникнуть состояние разрушения, пластического течения и др. Такова особенность «жесткости» этой модели и, как следствие, причина иногда наблюдаемых ее противо- речий с экспериментами и практикой, особенно в случаях ее непра- вильного, неразумного применения.