Транспортная задача на сети до

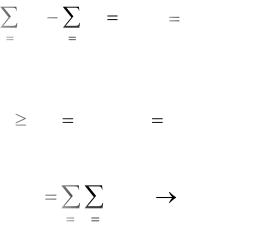
ТРАНСПОРТНАЯ ЗАДАЧА НА СЕТИ 5.1 ПОСТАНОВКА ЗАДАЧИ

Задача минимизации затрат на перевозки или минимизации величины суммарного пробега может быть решена не только в матричной, но и в сетевой постановке. Такой метод обладает большей наглядностью, так как распределение грузопотоков наносят непосредственно на реальную сеть железной дороги. Станции погрузки, разгрузки и транзитные станции являются вершинами сети, а проездные участки ее дугами. На каждой дуге указывается стоимость перевозки единицы груза (или расстояние в километрах). Если затраты на перевозку между двумя станциями в прямом и обратном направлении различны, то между ними проводят две дуги с разной стоимостью. У вершин сети указывают количество груза на станциях отправителях и потребности в нем (со знаком минус) на станциях потребителях.

Требуется так распределить грузопотоки, чтобы переместить весь груз с наименьшими затратами.

5.2 МАТЕМАТИЧЕСКАЯ МОДЕЛЬ

Обозначим перевозку от i-й станции на j-ую как xij . Так как

необходимо учитывать возможность движения и в противоположном направлении xji , то число переменных задачи будет равно удвоенному числу

дуг задачи.

Ограничения задачи записываются исходя из условий баланса для каждой вершины – суммарный грузопоток на i-ую станцию минус суммарный поток из нее равен объему выгруженного груза (выгрузке) Ri на

этой станции. Выгрузка для станций получателей положительна и равна потребности в грузах, а для отправителей отрицательна и равна по абсолютной величине запасам.

k	k
xji	xij Ri i 1,2,...n ,	(5.1)
j 1	j 1

где k – число связей (дуг) для i-той вершины. При этом выполняется условие неотрицательности переменных:

xij 0,(i 1,2,...n; j 1,2,...n)

Функция цели задачи по критерию минимума суммарных затрат –

n	n
F (x)	Cij xij min	(5.2)
i 1 j	1

Заметим, что данная модель не учитывает возможные ограничения на пропускную способность участков сети. Если возникает необходимость это

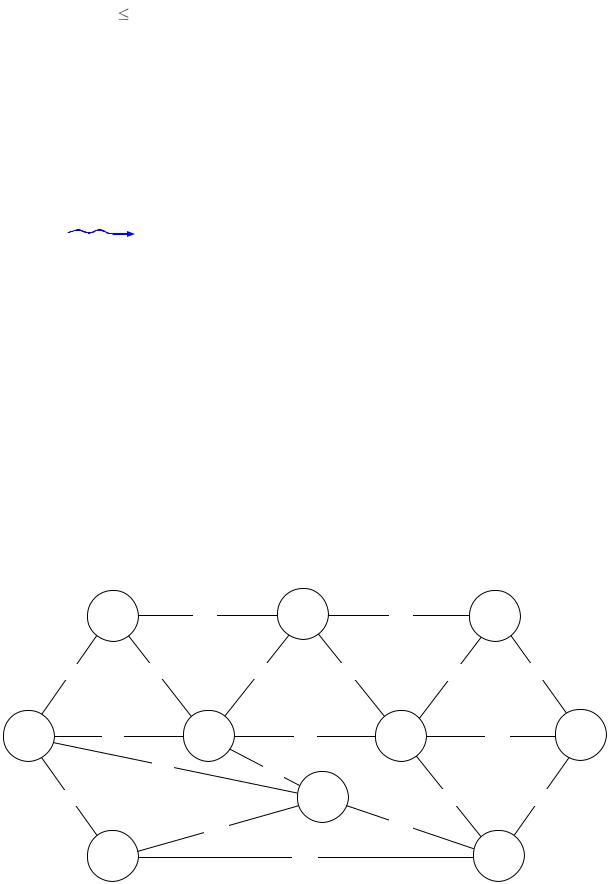
учесть, то в условие задачи вводят дополнительные ограничения в виде неравенств xij dij , где dij – пропускная способность дороги на участке

между станциями Bi и Bj .

5.3 ПОСТРОЕНИЕ НАЧАЛЬНОГО ПЛАНА ЗАДАЧИ

Распределим перевозки так, чтобы весь груз был вывезен, все потребности удовлетворены. Грузовые потоки указываются стрелками вдоль дуг с величинами количества перевозимого груза.

Введем обозначения:

					– стоимость перевозки единицы продукции,
		45
30					– направление и количество грузоперевозки,
(+60), (–20)					– запасы или потребности грузов на i-той станции.

Общее число загруженных дуг должно быть равно n – 1, где n – число вершин сети. Если загруженных дуг меньше, то следует ввести на одной из дуг фиктивную (нулевую) перевозку. Совокупность загруженных дуг не должна образовывать замкнутый цикл на сети, для этого, по-возможности, нужно обеспечивать одного потребителя от одного поставщика. Рассмотрим такое распределение на примере.

Пусть имеется схема железнодорожной сети, состоящей из десяти станций, для каждой из которых указаны запасы груза (со знаком плюс) или потребности в нем (со знаком минус). На каждой дуге показана стоимость грузоперевозки единицы груза для соответствующего проездного участка.

Объем запасов грузов на станциях B3 , B6 и B9		равен количеству
потребностей грузов на оставшихся станциях (рис. 5.1).
(–25)	(–25)	(+80)

В2

55

В4

40

В6

45	40	40	45	50	60
(–30)		(+60)		(–35)	(–30)

В1

50

В3

40

В5

40

В7

	45	30
40		В8
		45

(–30)	45	50
	45

(+55) В9

70

В10 (–20)

Рис. 5.1.

Составим первоначальный план грузоперевозок для удовлетворения потребностей грузов на станциях сети.

Вывезем груз со станции В9 (весь запас равен 55 ед.), 30 ед. на станцию В1, 5 ед. на станцию В8 (останется потребность 30-5=25ед.), 20 ед. на станцию

В10. Теперь вывезем груз (60 ед.) со станции В3: 25 ед. на станцию В2, 10 ед. на станцию В4 (осталось – 25-10=15), 25 ед. на станцию В8 (весь груз на эту

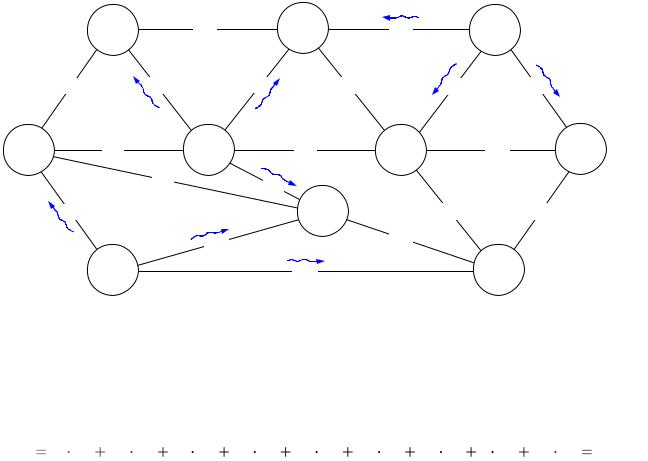
станцию доставлен). Вывозим груз со станции В6: 15 ед. на станцию В4 (все потребности здесь удовлетворены), 30 ед. на станцию В7, 35 ед. на станцию В5 и т. д. (рис. 5.2).

	(–25)				(–25)			(+80)
	В2		55		В4	15		В6
	155				155	40		115
							35		30
45	40			40		45	50		60
(–30)	25		(+60)	10		(–35)			(–30)
В1	50		В3		40	В5		40	В7
140			115			165			175
				25
	45				30
40					В8	(–30)	45		50
					145
30		5	45			45
(+55)	В9				20			В10	(–20)
	100				70			170
					Рис. 5.2.
В полученном		начальном			плане	перевозок	весь	груз	вывезен,	и
потребители получают необходимое им количество груза, при этом
загружено девять дуг при десяти вершинах (план не вырожден). Суммарная
стоимость перевозок равна:

F(x) 15 40 25 40 10 40 35 50 30 60 25 30 30 40 5 45 20 70 9125

.

Полученный план общей стоимости перевозок грузов, возможно, не является оптимальным.

5.4 МЕТОД ПОТЕНЦИАЛОВ УЛУЧШЕНИЯ ПЛАНА

Проверим полученный план перевозок методом потенциалов и при необходимости улучшим его.

Введем условные величины, приписываемые каждой вершине сети и называемые потенциалами станций Vi . Их численные значения могут быть

определены из решения двойственной к данной задаче. По теоремам двойственности план будет оптимальным, если выполнены условия

Vj Vi

cij

(5.3)

для занятых дуг (базисных переменных)

Vj Vi

cij

(5.4)

и для свободных дуг (свободных переменных).

Таким образом, разность между потенциалами для двух станций, между которыми есть грузоперевозки, равна стоимости перевозок на этой дуге. Для свободных дуг она должна быть меньше или равна стоимости перевозок.

Один из потенциалов следует задать произвольно, так же, как и в задаче в матричной постановке. Пусть V9 = 100, тогда, следуя по загруженным дугам, прибавляем к потенциалу стоимость перевозки при попутном грузопотоку движении и вычитаем стоимость при перемещении против потока, получим

	V8		100 45 145, V3										145 30 115 (так как грузопоток идет в
противоположном направлении).
	V2		115							40	155,	V4	115 40	155,	V6		155					40	115,
V5	115		50							165 ,
V7	115 60 175, V1 100 40 140, V10														100		70					170 .
	Проверим выполнение условия оптимальности (3.4) на свободных
дугах.
			V2							155	140	15	45,			V4	V2					155 155 0 55 ,
		V1
			V3							140	115	25	50 ,			V1	V8					145	140	5	45 ,
		V1
			V5							165	115	50	40	10 ,
		V3
			V5							165	155	10	45 ,			V5	V7					175 165 10 45 ,
		V4
			V5							170	165	5 45 ,				V10	V8					170	145	25	45,
		V10
			V7							175	170	5	50
		V10
	Условие оптимальности нарушено лишь на одной дуге В3 – В5 , для
которой невязка											10. Если таких дуг больше, то для пересчета необходимо
выбрать дугу с наибольшей невязкой.
	Введем на дуге В3 – В5												перевозку x35			, с направлением от вершины

с меньшим потенциалом к вершине с большим, при этом образуется замкнутый цикл загруженных дуг В3 – В5 – В6 – В4 – В3 . Причем, движение

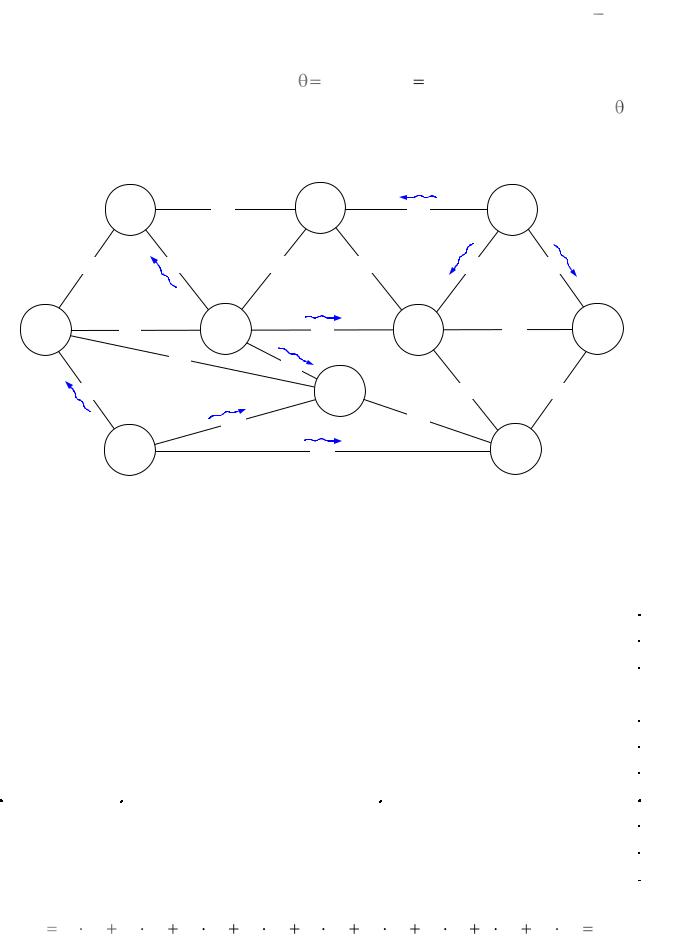
идет только по загруженным дугам, исключая одну незагруженную В3										В5 .
Двигаясь в направлении вновь введенного грузопотока по циклу, отметим все
перевозки в противопотоках и выберем из них минимальную. Присвоим это
численное	значение	величине			min{10,35} 10 .		Вычитая	из	всех
противопотоков и прибавляя ко всем попутным потокам груза величину										,
получим новый опорный план задачи.
	(– 25)				(– 25)		(+80)
	В2		55		В4	25	В6
	155				145	40	105
							25	30
45	40			40		45	50	60
(– 30)	25		(+60)			(– 35)			(– 30)
В1	50		В3		10	В5	40		В7
140			115		40	155			165
				25
	45				30
40					В8	(– 30)	45	50
					145
30		5	45			45
(+55)	В9				20		В10	(– 20)
	100				70		170

Рис.5.3

Вычислим потенциалы вершин из условий 5.3 и убедимся, что условия 5.4 также выполняются. Полученный оптимальный план представлен в таблице.

			Таблица 5.1
№	ДУГИ		ПЕРЕВОЗКИ
1	В9 – В1		30
2	В9 – В8		5
3	В9 – В10		20
4	В3 – В2		25
5	В6 – В5		25
6	В3 – В5		10
7	В3 – В8		25
8	В6 – В4		25
9	В6 – В7		30
Суммарная стоимость грузоперевозок является наименьшей и равна
F(x) 25 40	25 40 25 50 30 60 10 40	25 30 30 40 5 45 20 70 9025