Математика типовик 3 модуль

этом фигура находится слева. Такой обход соответствует возрастанию параметра.

Площадь искомой петли находим по формуле

		1	2		1	6	2	(6 − )2		27
	=		∫	( ′ − ′ ) =		∫			=		.
		2			2			24		5
			1			0

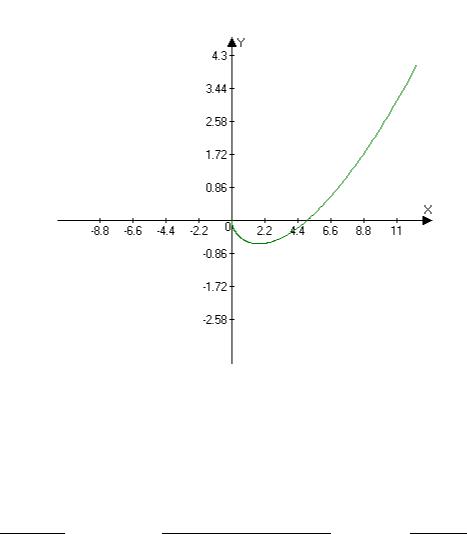
Задача 6. Найдите площадь, заключённую между осью Ox и верзиерой, определяемой уравнениями

= ,

{3

= 2 + 2 .

Рисунок 6

Решение. Значение аргумента x изменяется от −∞ до + ∞. Кривая симметрична относительно оси Oy. Так как параметр также меняется от −∞ до + ∞, то для вычисления площади используем несобственный интеграл с бесконечными пределами:

+∞

3

+∞

1

+∞

= ∫

= 3

∫

= 3

∙

|

2 + 2

2 + 2

−∞

−∞

−∞

= 2[ (+∞) − (−∞)] = 2 [

−

(−

)] = 2.

2

2

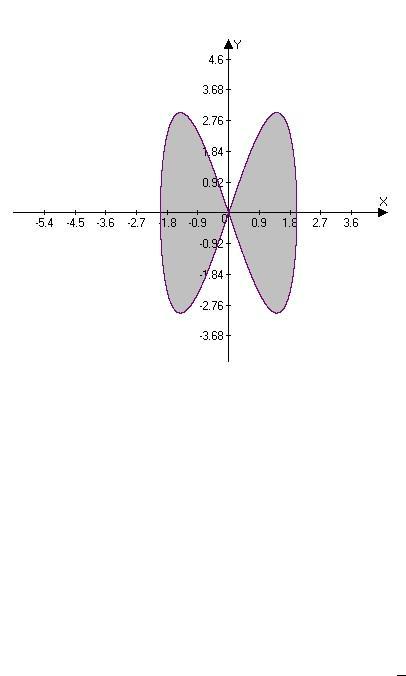
Задача 7. Вычислите площадь фигуры, ограниченной кривой

= sin , { = sin 2 .

Рисунок 7

Решение. Для построения кривой учтем, что она симметрична относительно осей координат. Действительно, если заменить на ( − ), то переменная x не меняется, а изменяет только свой знак; следовательно, кривая симметрична относительно оси . При замене же на ( + ) переменная не меняется, а меняет только свой знак. Это значит, что кривая симметрична относительно оси

.

Обе функции ( ) и ( ) имеют общий период 2. Поэтому достаточно рассмотреть отрезок изменения параметра [0, 2 ]. Общий вид кривой

изображён на рисунке 7. При изменении параметра от 0 до обе функции

2

сохраняют принимают неотрицательные значения. При этом ( ) возрастает на

	всем промежутке, а ( ) возрастает при 0 ≤ <		и убывает при		< ≤		.
		4		4		2

Далее на отрезке изменения параметра [2 ; 34 ] обе функции убывают, имея

при этом различные знаки. И, наконец, при [	3	; ]	функция ( )
4

продолжает убывать, в то время как функция ( ) уже возрастает. В силу симметричности фигуры относительно осей координат нам достаточно найти площадь четверти фигуры. Тогда искомая площадь будет равна полученному результату, умноженному на 4:

/2

/2

/2

= 4 ∫ ′ = 4 ∫ ∙ sin 2 ∙ ∙ cos = 8 ∫ sin cos2

0	0		0
	/2		cos3	/2
	= −8 ∫	cos2 (cos ) = −8			=	8	.
				|
			3			3
	0			0

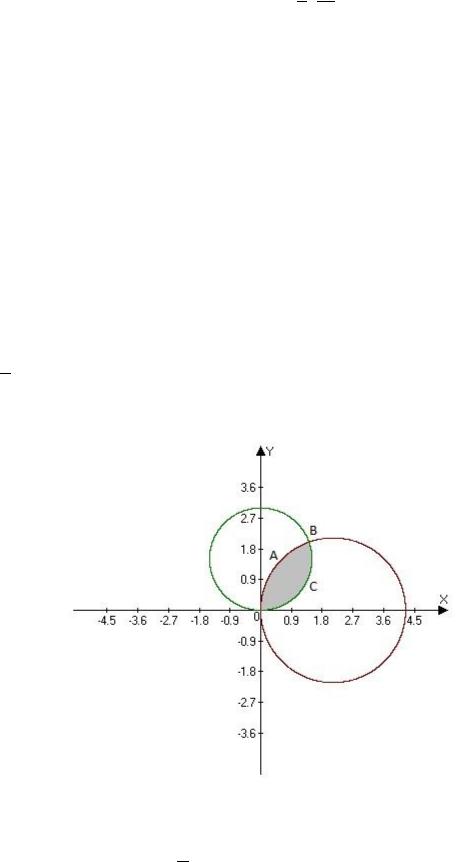
Задача 8. Вычислите площадь фигуры, ограниченной окружностями

= 3√2 cos и = 3 sin .

Рисунок 8

Решение. Окружность = 3√2 cos лежит в правой полуплоскости, проходит через полюс = 0, касаясь вертикальной прямой. Вторая окружность = 3 sin лежит в верхней полуплоскости, также проходит через полюс = 0,

касаясь гоизонтальной прямой. Очевидно, что полюс является точкой пересечения окружностей. Вторую точку пересечения находим из уравнения

3√2 cos = 3 sin .

Откуда ( √2, √6). Из рисунка 8 видно, что искомая площадь представляет собой сумму двух сегментов и . Отрезок [ ] лежит

на луче = √2. Таким образом, сегмент ограничен дугой первой

и отрезком [ ],

окружности

при

√2 ≤ ≤

а сегмент

–

2

отрезком [ ] и дугой второй окружности при 0 ≤ ≤ √2.

Поэтому

имеем

2

= 92

cos2 = 92 (

−

√2

),

∫

− √2

2

3

√2

√2

9

2

2

9

2

√2

=

∫

sin

=

( √2 −

),

2

4

3

0

9

=

+

=

2( − √2

−

√2).

4

Задача 9. Вычислите

длину

дуги

у кривой

=

1

2 −

1

ln , заключённой

4

2

между точками с ординатами = 1 и = 2.

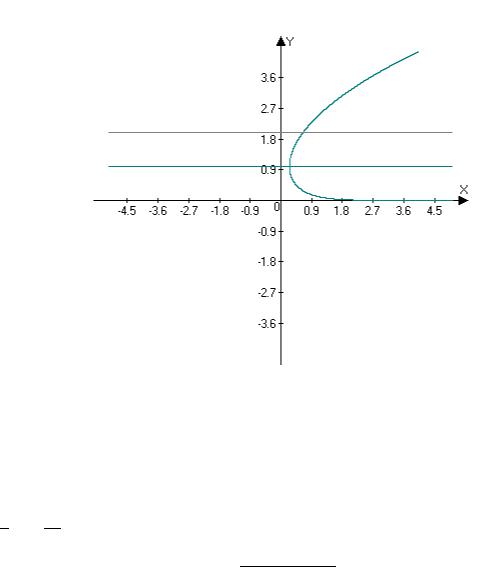
Рисунок 9

Решение. Здесь удобнее рассматривать в качестве независимой переменную . Тогда найдём производную функции ( ) по переменной :

′ = 12 − 21 ,

							1				1			2		1		1
√1 + ′2 = √(								+				)		=			+				.
							2				2					2			2
Длину дуги вычислим по формуле:
2							2		1					1				3				1
= ∫ √			= ∫ (												) =					+			ln 2.
	1 + ′2									+
																		4				2
1					1			2					2
Задача 10. Вычислите длину дуги кривой = ln cos ,																						заключённой между
точками с абсцисами = 0 и =						.
					4

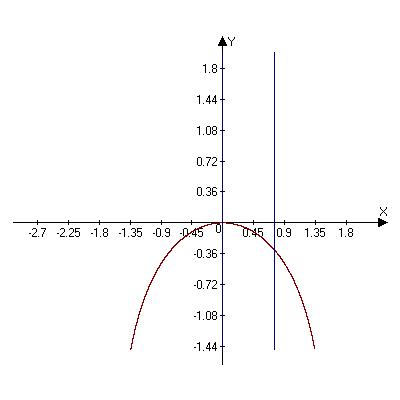
Рисунок 10

														=		1
	Решение. Поскольку ′ = − , то √1 + ′2								= √1 + 2								. Тогда длина
																cos
	дуги равна
	4								/4				3
	= ∫		= ln (			+		)|0		= ln					.
		cos			4		2						8
	0
										3
	Задача 11. Найдите длину замкнутой кривой							= sin				.
										3

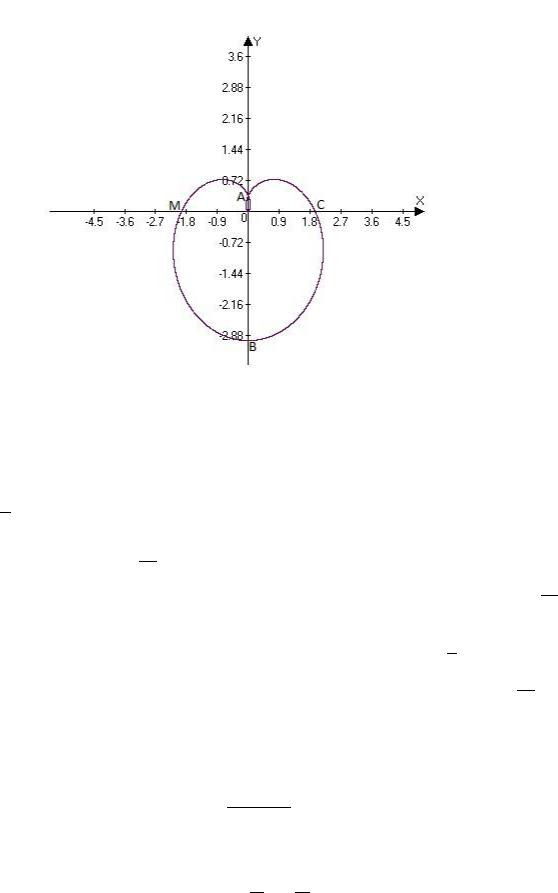
Рисунок 11

Решение. Кривая задана в полярных координатах. Найдём границы изменения угла . Так как – расстояние, то должно выполняться неравенство ≥ 0. И

значит sin 3 ≥ 0. Отсюда 0 ≤ ≤ 3 .

При изменении от 0 до 3 длина радиус-вектора возрастает от 0 до , а

2

конец радиус-вектора описывает дугу (рис.11). Когда меняется от 3

2

до 3 величина убывает от до 0 (дуга ). Таким образом получаем замкнутую кривую, симметричную относительно прямой = ± π2. Значит для

вычисления длины кривой мы можем найти половину ее длины (0 < < 32 ) и результат умножить на 2.

Длину находим по формуле

2

= ∫ √ 2 + ′2.

1

′ = sin2 3 cos 3,

														= a sin2						,
					= √ 2 sin6			+ 2 sin4				cos2
√ 2				+ ′2
				3					3			3					3
3 /2	2				3 /2																3 /2
									2						3		2						3
= ∫ sin				= ∫ (1 − cos						) = ( −						sin			)|0			=		.
	3								3						2		3						2
0				0

Задача 12. Вычислите длину логарифмической спирали = от некоторой её точки ( 0, 0) до переменной точки ( , ).

Рисунок 12

Решение. В этом случае, поскольку мы не знаем, какая из величин 0 или больше, то находим длину дуги как модуль интеграла

= | ∫ √ 2 + ′2 | = | ∫ √ 2 2 + 2 2 2 | = √1 + 2 | ∫ |

0 0 0

=	√1		+ 2	| − 0| =	√1		+ 2	| − |.
								0

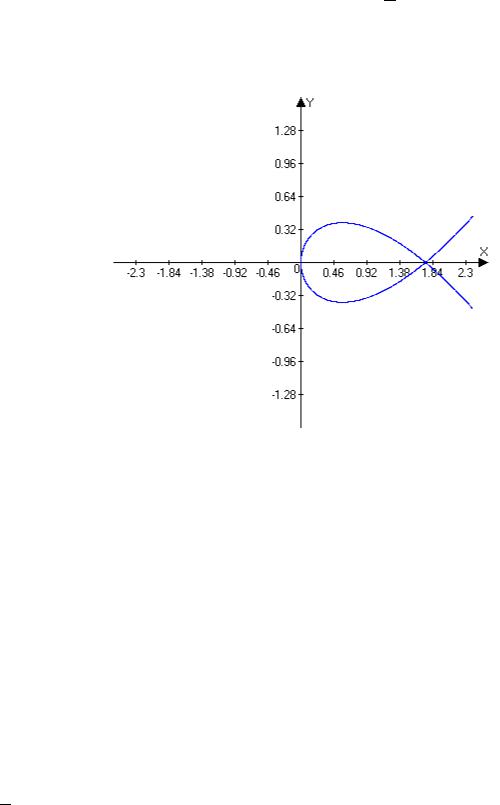
Таким образом, длина дуги логарифмической спирали пропорциональна приращению полярного радиуса дуги.

Задача 13. Вычислите длину петли кривой { = √3 2,= − 3.

Рисунок 13

Решение. Найдём пределы интегрирования. Обе функции ( ) и ( ) определены при всех значениях параметра . Кроме того, ( ) – чётная и неотрицательная, а ( ) меняет знак и нечётная. Поэтому кривая расположена в правой полуплоскости, симметрично относительно оси абсцисс. Определим точки самопересечения кривой:

( 1) = ( 2),
{ ( )				= ( ).
	1			2
			2
	√3			= √3 2			,
	1			2
{ − 3				= − 3.
1	1			2			2

Решение системы даёт единственную точку самопересечения кривой, а именно (√3, 0) при значениях параметра = ±1. Таким образом, границами интегрирования являются значения параметра 1 = −1, 2 = 1. Длину дуги вычисляем по формуле:

2

1

1

= ∫ √ ′2 + ′2 = ∫ √(2√3 )2 + (1 − 3 2)2 = ∫(1 + 3 2) = 4.

1

−1

−1

Раздел 3.

НЕСОБСТВЕННЫЕ ИНТЕГРАЛЫ

Задание 13. Нахождение несобственных интегралов:

а) по бесконечному промежутку интегрирования, б) от неограниченной на отрезке функции.

А. Напомним, что несобственные интегралы по бесконечному промежутку определяются посредством предельного перехода.

Если функция ( ) непрерывна на промежутке [ , +∞), то

+∞
∫	( ) =	lim ∫ ( )
		→+∞
Если функция ( ) непрерывна на промежутке (−∞, ], то
∫	( ) =	lim ∫ ( )
−∞		→−∞
Если функция непрерывна на всей числовой оси, то
+∞		+∞
∫ ( ) = ∫ ( ) + ∫			( ) , .
−∞	−∞

Если предел существует и конечен, то несобственный интеграл называют сходящимся, если же предел не существует или бесконечен, то интеграл называют расходящимся.

Пример 1. Найдите значение несобственного интеграла или установите его расходимость: ∫0+∞ cos .

Решение. По определению несобственного интеграла имеем

+∞
∫ cos =	lim	∫ cos =	lim sin |0 =	lim (sin − sin 0)
0	→+∞ 0		→+∞	→+∞
=	lim	sin

→+∞

Так как этот предел не существует, несобственный интеграл расходится.