5.8. Укладки графов. Укладка графов в трехмерном пространстве

Определение. Граф G обладает укладкой в некотором пространстве, если он изоморфен некоторому графу , изображенному в этом пространстве при помощи точек (представляющих вершины) и жардановых кривых (представляющих ребра), причем никакие 2 кривые нигде не пересекаются друг с другом, кроме инцидентной им обеим вершины.

Теорема 1. Каждый конечный граф может быть уложен в трехмерном пространстве.

Доказательство:

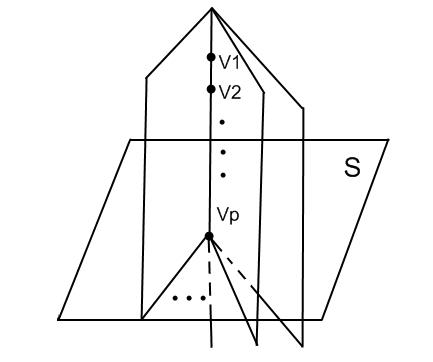
Пусть в графе G вершин. На прямой, перпендикулярной плоскостиS, расставляем все p вершин. Пусть множество ребер E состоит из ребер . Через прямую, на которой расставлены всеp вершин, проводим q плоскостей, перпендикулярных нашей плоскости S. Затем каждое ребро проводим на отдельной плоскости. Пересечений у этих ребер не будет, кроме вершин. В нашем доказательстве мы предъявили укладку в трехмерном пространстве. Теорема доказана.

5.9. Планарность. Формула Эйлера для плоских графов

Определение. Граф называется плоским, если он уложен на плоскости.

Определение. Граф называется планарным, если он изоморфен некоторому плоскому графу.

Пример: Пусть даны графы G и H, где G – плоский, H – не плоский, но планарный, так как .

Плоский граф разбивает нашу плоскость на области, которые называются гранями. Грани бывают ограниченными и неограниченными. В дальнейшем грани будем обозначать через , а число граней– через m.

Пример. Пусть дан граф:

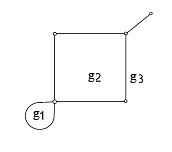
где g₁, g₂ – ограниченные грани, g₃ – неограниченная грань.

Теорема 2 (формула Эйлера). Пусть G – связный плоский граф, у которого p вершин, q ребер и m граней, тогда имеет место соотношение, что

p + m = q + 2. (2)

Доказательство (индукцией по q):

Пусть q=0, тогда граф имеет 1 вершину, т.е. p = 1, m = 1, так как грань только одна – неограниченная. Соотношение (2) справедливо, 1 + 1 = 0+ 2.

Пусть соотношение (2) справедливо для графа, число рёбер которого меньше q.

Теперь докажем справедливость соотношения (2) для графа с q рёбрами.

Рассмотрим произвольное ребро e графа G. Возможны 2 случая:

1) – петля. Тогда из графа G удалим это ребро e, получим граф, у которого p вершин, q–1 ребер, m–1 граней. Но поскольку по индукционному предположению верна формула Эйлера, то p+m–1 = q–1+2. Прибавив 1 слева и справа, получим нашу формулу: p+m = q+2.

2) , где . Удаляем ребро e, получаем граф H. Возможны 2 случая:

а)

Граф H – связный, значит, мы можем прийти из вершины в вершину по другому маршруту. У графа H p вершин, (q–1) ребер и (m–1) граней, т.е. число граней уменьшается, так как вершины и лежат в разных гранях, а после удаления ребра е грани сливаются. Мы получили случай, аналогичный первому.

б)

Граф H – несвязный, т.е. после удаления ребра е получаем 2 связные компоненты графа H₁, H₂: H₁ = (p₁,q₁,m₁), H₂ = (p₂,q₂,m₂). Для H₁ и H₂ справедлива формула Эйлера по индукционному предположению p₁+m₁ = q₁+2, p₂+m₂ = q₂+2, p₁+p₂ = p, q₁+q₂ = q–1, m₁+m₂ = m+1, так как вместо одной бесконечной грани стало 2. Сложим наши равенства:

p₁+p₂+m₁+m₂ = q₁+q₂ +4 p+m+1 = q–1+4p+m = q+2.

Теорема доказана.