2004-matematicheskiy-analiz-differencial-noe-ischislenie-funkciy-odnoy-peremennoy-5mb

Решение

Неопределенность вида

0

. Так как sin α(x) ~ α(x) при α(x) → 0,

0

то sin (5x) ~ 5x при x → 0. Тогда

lim

sin(5x)

= lim

5x

= 5.

x

→0

x

x→0

x

Пример 1.6.21

Вычислить lim

sin(x + 1)

.

x→−1 2(x + 1)

Решение

Неопределенность вида

0

. Так как sin α(x) ~ α(x) при α(x) → 0,

0

то sin (x + 1) ~ (x + 1) при x → −1. Тогда

lim

sin(x + 1)

=

1

lim

x + 1

=

1

.

x→−1 2(x + 1)

2 t→0 x + 1 2

Пример 1.6.22

Вычислить lim

tg(2x)

.

x→0 3x

Решение

Неопределенность вида

0

. Так как tg α(x) ~ α(x) при α(x) → 0,

0

то tg (2x) ~ 2x при x → 0. Тогда

lim

tg(2x)

= lim

2x

=

2

.

x

→0 3x

x→0 3x 3

Пример 1.6.23

Вычислить lim

e− x − 1

.

x→0 2x

Решение

Неопределенность вида

0

. Так как eα(x) − 1 ~ α(x) при α(x) → 0,

0

то e−x − 1 ~ −x при x → 0. Тогда

e− x

− 1

− x

1

lim

= lim

= −

.

2

x→0 2x

x→0 2x

61

Пример 1.6.24

Вычислить lim

cos(8x) − cos x

.

x→0

1− cos(3x)

Решение

Выражение, стоящее в числителе, преобразуем по формуле

cosα − cosβ = −2sin

α + β

sin

α − β

;

2

2

cos(8x) − cos x

−2sin

8x + x

sin

8x − x

−2sin

9x

sin

7x

lim

= lim

2

2

= lim

2

2

.

1− cos(3x)

1− cos(3x)

x→0 1− cos(3x)

x→0

x→0

Неопределенность вида 0 . Так как sin α(x) ~ α(x), а 1 − cos α(x) ~

~ α2(x)/2

при α(x)

0

→ 0, то sin

(9x/2) ~ 9x/2,

sin (7x/2) ~ 7x/2,

1 − cos (3x) ~ 9x2/2 при x → 0. Тогда

−2sin

9x

7x

−2

9x 7x

lim

sin

= lim

= lim −63x2

= −

63

= −7.

2

2

2

2

9x2

x→0

1− cos(3x)

x→0

x→0 9x2

9

2

Пример 1.6.25

Вычислить lim arctg(2x) . x→0 sin(5x)

Решение

Неопределенность вида 0 . Так как arctg α(x) ~ α(x) и sin α(x) ~ α(x)

0

при α(x) → 0, то arctg (2x) ~ 2x, а sin (5x) ~ 5x при x → 0. Тогда

	lim	arctg(2x)		= lim	2x	=	2	.
	x→0	sin(5x) x→0 5x 5
Пример 1.6.26
1− cos3 x
Вычислить lim			.
x→0 xsin(2x)

62

Решение

Разложим числитель на множители по формуле разности кубов a3 – b3 = (a – b)(a2 + ab + b2):

1− cos3		x	= lim	(1− cos x)(1+ cos x + cos2 x)
lim					.
x→0 xsin(2x)			x→0	xsin(2x)

Неопределенность вида 0 . Так как sin α(x) ~ α(x) , а 1 − cos α(x) ~

0

~ α2(x)/2 при α(x) → 0, то sin (2x) ~ 2x, 1 − cos x ~ x2/2 при x → 0. То-

гда

(1− cos x)(1+ cos x + cos2 x)

x2

(1+ cos x + cos2 x)

lim

= lim

2

=

x→0

xsin(2x)

x→0

x 2x

= lim

1+ cos x + cos2

x

=

3

.

4

4

x

→0

Пример 1.6.27

Вычислить lim

2x

− e3x

.

x→0 arcsin(3x)

Решение

В числителе прибавим и отнимем 1, а затем разложим на сумму двух пределов:

lim	2x − e3x	= lim	2x − 1+ 1− e3x	= lim	2x − 1	+ lim	1− e3x	.
x→0 arcsin(3x)		x→0 arcsin(3x)		x→0 arcsin(3x)		x→0 arcsin(3x)

В каждом из полученных пределов неопределенность вида 0 . Так

0

как arcsin α(x) ~ α(x) при α(x) → 0, то arcsin (3x) ~ 3x при x → 0. Так как aα(x) – 1 ~ α(x)ln a, а eα(x) – 1 ~ α(x) при α(x) → 0, то 2x − 1 ~ xln2,

а e3x – 1 ~ 3x при x → 0. Тогда

lim	2x − 1	+ lim	1− e3x	= lim	x ln 2	− lim	3x	=	ln 2	− 1.
									3
x→0 arcsin(3x)		x→0 arcsin(3x)		x→0 3x		x→0 3x

63

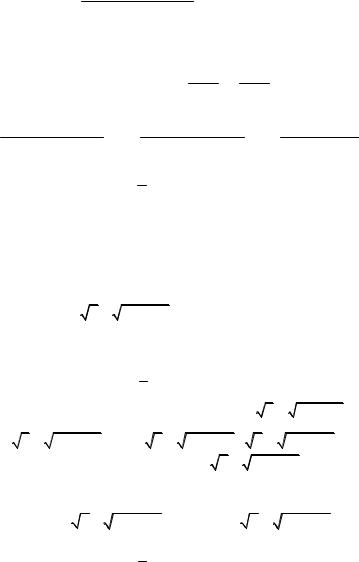
Пример 1.6.28

Вычислить lim cos(7x) − cos(9x) .
x→0	x2

Решение

Выражение, стоящее в числителе, преобразуем по формуле

cosα − cosβ = −2sin α + β sin α − β : 2 2

lim cos(7x) − cos(9x) = lim −2sin(8x)sin(− x) = lim 2sin(8x)sin x .
x→0	x2	x→0	x2	x→0	x2

Неопределенность вида 0 . Так как sin α(x) ~ α(x) при α(x) → 0, то

0

sin (8x) ~ 8x, а sin x ~ x при x → 0. Тогда

lim		2sin(8x)sin x	= lim		2 8x x	= 16.
		x2
x→0				x→0 x2
Пример 1.6.29
Вычислить lim		2 − 1+ cos x		.
x→0		sin2 x

Решение

Неопределенность вида 0 . Умножим числитель и знаменатель на

0

выражение, сопряженное к числителю, т.е. на 2 +

1+ cos x :

lim

2 − 1+ cos x

= lim

(

2 −

1+ cos x)(

2 +

1+ cos x)

=

sin2 x

sin2 x( 2 +

x→0

x→0

1+ cos x)

= lim

2 − 1− cos x

= lim

1− cos x

.

x→0 sin2 x( 2 +

1+ cos x)

x→0 sin2 x(

2 + 1+ cos x)

Неопределенность вида 0 . Так как sin α(x) ~ α(x) , а 1 − cos α(x) ~

0

α2(x)/2 при α(x) → 0, то sin 2 x ~ x2, 1 − cos x ~ x2/2 при x → 0. Тогда

64

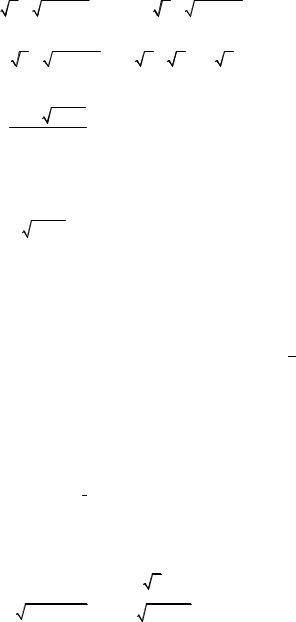
		1− cos x					x2
lim				= lim		2			=
		2 +				2 + 1+ cos x)
x→0 sin2 x(			1+ cos x) x→0 x2 (

	= lim		1
		2( 2	+ 1+ cos x)
	x→0

Пример 1.6.30

Вычислить lim e4 x − 3 1− 9x . x→0 ln(1+ sin x)

=		1	=		1	.
		2 + 2)			2
2(			2

Решение

В числителе прибавим и отнимем 1, а затем разложим на разность двух пределов:

1

lim

e4x − 3

1− 9x

= lim

e4x −1+1− (1− 9x)

3

=

ln(1+ sin x)

x→0 ln(1+ sin x)

x→0

1

= lim

e4x

− 1

− lim

(1− 9x)

3

− 1

.

x→0 ln(1+ sin x)

x

→0 ln(1+ sin x)

В каждом из полученных пределов неопределенность вида 0 .

0

Так как ln(1 + α(x)) ~ α(x) при α(x) → 0, то ln(1 + sin x) ~ sin x при

x → 0.

Так как eα(x) – 1 ~ α(x) при α(x) → 0, то e4x – 1 ~ 4x при x → 0.

Так как (1 + α(x))m – 1 ~ mα(x) при α(x) → 0, то (1 – 9x)1/3 – 1 ~ (− 9x)/3

при x → 0. Тогда

1

lim

e4x − 1

− lim

(1− 9x)3 − 1

= lim

4x

− lim

(−3x)

= 4

+ 3

= 7.

+ sin x)

sin x

x→0 ln(1

x→0 ln(1+ sin x)

x→0 sin x x→0

Пример 1.6.31

(e−4x3 − 1)(1− cos

x )

Вычислить lim

.

(

1+ 2xsin x − 1)(1−

cos(3x) )

x→0

65

Решение

Неопределенность вида 0 . Умножим числитель и знаменатель на

0

(1+ 1+ cos(3x) ):

lim

(e−4x3 − 1)(1− cos

x )

=

1+ 2xsin x − 1)(1−

cos(3x) )

x→0 (

= lim

(e−4 x3

− 1)(1− cos

x )(1+ cos(3x) )

=

( 1+ 2xsin x − 1)(1−

cos(3x) )(1+

cos(3x) )

x→0

= lim

(e−4x3

− 1)(1− cos

x )(1+ cos(3x) )

.

x→0

(

1+ 2xsin x − 1)(1− cos(3x))

Так как 1 − cos α(x) ~ α2(x)/2 при α(x) → 0, то 1 − cos(3x) ~ 9x2/2, а 1 − cos x ~ x/2 при x → 0.

Так как eα(x) – 1 ~ α(x) при α(x) → 0, то e−4x3 – 1 ~ −4x3 при x → 0.

Так как (1 + α(x))m – 1 ~ mα(x) при α(x) → 0, то (1 + 2x sin x)1/2 – 1 ~ ~ (2x sin x)/2 = x sin x при x → 0.

Тогда

− 1)(1− cos x )(1+

(e−4x3

cos(3x) )

(−4x3 )

x

(1+ cos(3x) )

lim

= lim

2

=

(

1+ 2xsin x − 1)(1− cos(3x))

9x2

x→0

x→0

xsin x

2

= lim

−4x4 (1+

cos(3x) )

=

sin x x

=

x→0

9x3 sin x

при x → 0

= lim

−4x(1+ cos(3x) )

= lim

−4(1+

cos(3x) )

= −

8

.

x→0

9x

x→0

9

9

Пример 1.6.32

Вычислить lim

tg(πx)

.

x→2 sin(2πx)

66

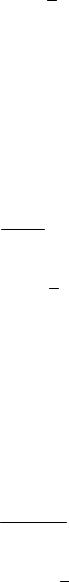
Решение

Неопределенность вида 0 . Внимание! Заменить tg(πx) и sin (2πx) на эк-

0

вивалентные бесконечно малые функции сейчас нельзя, так как πx → 2π, а 2πx → 4π при x →2. Сделаем замену x – 2 = t, тогда x = t + 2 и t →0:

lim

tg(πx)

= lim

tg(π(2 + t))

= lim

tg(2π + πt)

=

x→2 sin(2πx)

t→0 sin(2π(2 + t))

t→0 sin(4π + 2πt)

= lim

tg(πt)

=

tg(πt) ~ πt,

= lim

πt

=

1

sin(2πt) ~ 2πt

.

t→0 sin(2πt)

при t → 0

t→0 2πt

2

Пример 1.6.33

Вычислить lim sin(3x) . x→π sin(2x)

Решение

Неопределенность вида 0 . Внимание! Заменить sin(3x) и sin(2x) на эк-

0

вивалентные бесконечно малые функции сейчас нельзя, так как 3x → 3π,

а 2x → 2π при x →π. Сделаем замену x – π = t, тогда x = t + π и t →0:

lim

sin(3x)

= lim

sin(3(t + π))

= lim

sin(3t + 3π)

= lim − sin(3t)

x→π sin(2x) t→0 sin(2(t + π))

t→0 sin(2t + 2π) t→0 sin(2t)

=

sin(3t) ~ 3t;

= lim −3t

= −

3

sin(2t) ~ 2t

.

при t → 0

t→0 2t

2

Пример 1.6.34

Вычислить lim 35x−3 − 32x2 . x→ 1 tg(πx)

Решение

Неопределенность вида 0 . Внимание! Заменить tg(πx) на

0

лентную бесконечно малую функцию сейчас нельзя, так как при x → 1. Сделаем замену x – 1 = t, тогда x = t + 1 и t → 0:

=

эквива-

πx → π

67

5x−3

2 x2

5(t +1)−3

−

2(t +1)2

5t+ 2

− 3

2t2 + 4t+ 2

lim

3

−

3

= lim

3

3

= lim

3

=

tg(

x)

tg(

(t + 1))

tg(

t

+

)

x→1

t→0

t→0

π

π

π

π

2

−1)

32t2 −t

−1 ~ (2t2 − t)ln3,

−35t+2 (2t2 − t)ln3

= lim

−35t+2 (32t

−t

=

tg(πt) πt

= lim

=

t→0

tg(πt)

при t → 0

t→0

πt

= lim −35t+ 2 t(2t − 1)ln 3 = lim −35t + 2 (2t − 1)ln 3 = −32 (−1)ln 3 = 9ln 3.

t→0	π	t	t→0	π	π	π

Пример 1.6.35

Вычислить lim 3 1+ ln2 x − 1 . x→1 1+ cos(πx)

Решение

Неопределенность вида 0 . Заметим, что при x → 1 функция ln2x → 0,

0

а значит, можно заменить бесконечно малую функцию (1 + ln2x)1/3 − 1 на эквивалентную ей при x → 1 бесконечно малую функцию ln2x/3:

3 1+ ln2

x − 1

1

ln

2

x

cделаем

замену:

lim

= lim

3

=

t = x − 1;

=

+ cos(πx)

x→1 1

x→1 1

+ cos(πx)

x = t+1 t

→ 0

(πt)2

cos(πt)~

,

1

ln2

(t +1)

1

ln2 (t +1)

2

2t2

2

=

lim

=

lim

=

ln(t+1)~t

= lim

=

.

+ cos(π(t +

1))

3π2

3 t→0 1

3 t→0 1− cos(πt)

при t → 0

t→0 3π2t2

Пример 1.6.36

Вычислить	lim	tg(x + 1)			.
	x→−1 e3 x3 −4x2 +6 − e
Решение
	tg(x + 1)		0					tg(x + 1)
lim			=				= lim		.
x→−1 e3 x3 −4x2 +6 − e			0				x→−1 e(e3 x3 −4 x2 +6 −1 − 1)

68

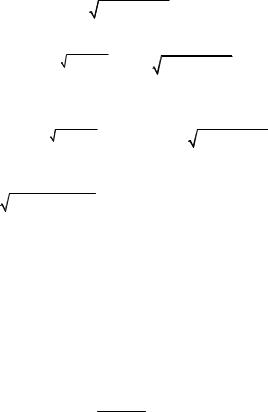
При x → −1, x + 1 → 0, а значит, tg (x + 1) можно заменить на эк- вивалентную бесконечно малую функцию x + 1. Так как при x → −1,

3 x3 − 4x2 + 6 − 1 → 0 ,

то

e3 x3 −4 x2 +6 −1 − 1 3 x3 − 4x2 + 6 − 1 .

Тогда

lim

tg(x + 1)

= lim

(x + 1)

=

x→−1 e(e3 x3 −4x2 +6 −1 − 1) x → −1 e(3 x3 − 4x2 + 6 − 1)

=

(x + 1)

=

x3 − 4x2 + 5 → 0 при x → −1, тогда

=

lim

1/ 3

1

(x3 − 4x2 + 5)

x → −1 e(3 1+ x3 − 4x2 + 5 −1)

(1+ x3 − 4x2 + 5)

−1

3

= lim

(x + 1)

=

3

lim

(x + 1)

.

(x3 − 4x2 + 5)

(x3 − 4x2 + 5)

x→−1 e

1

e x→−1

3

Разложим выражение, стоящее в знаменателе на множители:

−	x3	− 4x2 + 5		x + 1
	x3	+ x2		x2 − 5x + 5.

− −5x2 + 5 −5x2 − 5x

−5x + 5

5x + 5

0

Тогда

3

lim

(x + 1)

=

3

lim

(x + 1)

=

(x3 − 4x2 + 5)

e x→−1

e x→−1 (x + 1)(x2 − 5x + 5)

=

3

lim

1

=

3

=

3

.

e x→−1 x2

− 5x + 5 e(1

+ 5 + 5) 11e

69

Пример 1.6.37

Вычислить lim(2 − esin x )ctg(πx) .

x→0

Решение

Неопределенность вида 1∞. Для того чтобы раскрыть эту неопре- деленность, представим основание в виде 1 + α(x), а в показателе вы- делим множитель 1/α(x):

lim(2 − esin x )ctg(πx) = lim(1+ 1− esin x )ctg(πx)		(1−esin x )
		1−esin x .
x→0	x→0

Так как по второму замечательному пределу

1

lim (1+ x)x = e ,

x→0

то

1

lim(1+ 1− esin x )1−esin x = e.

x→0

Тогда

lim(1+ 1− esin x )

ctg(πx)

(1−esin x )

sin x

)

lim

1−esin x

π

lim ctg( x)(1−e

= ex→0

1−esin x

= ex→0

tg(πx)

x→0

tg(πx) ~ πx,

− lim

sin x

sin x~x

− lim

x

=

1− esin x ~ − sin x

=

= e x→0

πx

при x → 0

= e x →0 πx = e

при x → 0

Пример 1.6.38

=

−1

π .

						1
	Вычислить lim(sin x + cos x)tgx .
	x→		π
		4
	Решение
		1											1
										2		2
	lim(sin x + cos x)tgx =										+			= 2.
		π								2		2
	x→
		4

70