2. УСЛОВИЕ ТЕКУЧЕСТИ
Рассмотренные в 1 простейшие математические модели
(ММ) пластического деформирования сплошной среды при одноосном нагружении позволяют подойти к выяснению условия, при выполнении которого начинают возникать пластические деформации в случае произвольного напряженного состояния. Это условие называют условием пластичности или условием текучести, поскольку процесс пластического деформирования среды часто называют пластическим течением.
Так как для упругой сплошной среды деформированное состояние в окрестности фиксированной точки однозначно определено тензором напряжений ̂ с компонентами ij (i, j = 1, 2, 3) и абсолютной температурой T и не зависит от последовательности нагружения, то условие текучести можно записать в виде
f1( ij,T) = 0.
Для материала, обладающего свойством деформационной изотропии, функция в левой части этого равенства должна одинаковым образом зависеть от главных напряжений , = 1, 2, 3.
Тогда можно записать f1( ,T) = 0, но возможна запись условия текучести и в виде
где I1 , I2 и I3 — |
f2 |
(I1 ,I2 ,I3 ,T) = 0, |
||
|
̂ ̂ ̂ |
|||
. |
̂ ̂ |
̂ |
первый, второй и третий инварианты тензора |
|
̂ |
До определенного уровня всестороннего сжатия или растя- |
|||
|
|
|
|
|
жения пластические деформации обычно не возникают. Поэтому влияние первого инварианта можно не учитывать и представить условие текучести в виде
|
|
|
|
|
f3 |
(I |
,I3s,T) = 0, |
|
|
(2.1) |
|||
|
|
1 |
2 |
|
|
|
2̂s |
1̂ |
|
2 |
3 |
|
|
где I2s |
= I2 − |
|
I1 , I3s |
= I3 − |
|
I1 I2 + |
|
I1 |
— второй и третий |
||||
3 |
3 |
27 |
|||||||||||
̂ |
̂ |
|
̂ |
̂ |
|
̂ |
|
̂ ̂ |
|
|
̂ |
|
|
инварианты девиатора напряжений ̂s.
Условие текучести |
15 |
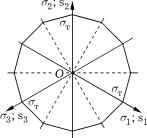
При фиксированной температуре (2.1) в трехмерном пространстве главных напряжений геометрически соответствует цилиндрической поверхности, называемой поверхностью текучести или поверхностью пластичности. Эта поверхность пересекает оси O в точках с координатами ± т(T), где т(T) — зависящий от температуры T предел текучести материала при растяжении. Образующая этой поверхности одинаково наклонена к осям O и перпендикулярна к плоскости, заданной уравнением 1 + 2 + 3 = 0 и называемой девиаторной плоскостью, поскольку любой лежащий в ней вектор соответствует девиатору напряжений для некоторого напряженного состояния. След пересечения этой плоскостью поверхности текучести образует кривую текучести (рис. 2.1), которая обладает следующими свойствами:
–если пластическая деформация не возникает с самого начала нагружения материала, то кривая не проходит через начало системы координат (в противном случае кривая текучести стягивается в точку, совпадающую с началом системы координат);
–луч, проведенный из начала системы координат, пересекает кривую текучести только один раз (иначе существовало бы два подобных напряженных состояния, удовлетворяющих условию начала пластического деформирования, что невозможно);
–кривая симметрична относительно проекций Os осей O на девиаторную плоскость;
–если свойства материала при растяжении и сжатии одинаковы, то кривая симметрична относительно штриховых прямых, перпендикулярных этим проекциям.
Рис. 2.1.
16 |
Условие текучести |
Из этих свойств следует, что кривая текучести должна состоять из 12 одинаковых дуг (см. рис. 2.1). Так как косинусы углов
между осями O и их проекциями на девиаторную плоскость
√
равны 2/3, то в этой плоскости эта кривая пересекает оси Os в точках с координатами
√
s = ± 2/3 т(T).
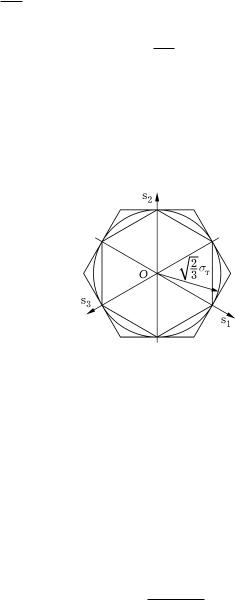
В 3 показано, что поверхность текучести должна быть выпуклой, откуда следует, что выпукла и кривая текучести, т. е. она должна быть заключена между двумя правильными шестиугольниками, пересекающими оси Os в тех же точках и симметричными относительно осей Os (рис. 2.2).
Рис. 2.2.
Внутренний шестиугольник образован пересечением девиаторной плоскостью граней призмы, заданных уравнениями
1 − 2 = ± т, 2 − 3 = ± т и 3 − 1 = ± т.
Приняв боковую поверхность этой призмы в качестве поверхности текучести, придем к условию текучести
max{| 1 − 2|, | 2 − 3|, | 3 − 1|} = т(T). |
(2.2) |
Если 1 > 2 > 3, то вместо (2.2) получим условие наибольшего касательного напряжения max = т/2, поскольку
max = ( 1 − 3).
2
Условие текучести |
17 |
Это условие не учитывает влияние промежуточного по значению главного напряжения 2.
Внешний шестиугольник (см. рис. 2.2) образован пересечением девиаторной плоскостью граней призмы с уравнениями
1 − с = ±2 т/3, 2 − с = ±2 т/3 и 3 − с = ±2 т/3,
где
с = ( 1 + 2 + 3) 3
— среднее напряжение. Если боковую поверхность этой призмы считать поверхностью текучести, то условие текучести примет вид
|
2 т(T) |
|
|
max{| 1 − с|, | 2 − с|, | 3 − с|} = |
|
. |
(2.3) |
3 |
|||
Его называют условием наибольшего приведенного напряжения.
Если поверхность текучести задать уравнением |
|
( 1 − 2)2 + ( 2 − 3)2 + ( 3 − 1)2 = 2 т2(T), |
(2.4) |
то ее пересечение девиаторной плоскостью будет представлять
√
собой окружность радиусом 2/3 т, вписанную во внешний шестиугольник и описанную вокруг внутреннего шестиугольника (см. рис. 2.2). С учетом равенства
|
9 N2 = ( 1 − 2)2 + ( 2 − 3)2 + ( 3 − 1)2 = 6I2s, |
||||||||
|
|
|
|
|
|
|
|
|
̂ |
|
|
2 |
|
|
|
|
|
||
где N = |
|
|
|
I2s — касательное октаэдрическое напряжение, вме- |
|||||
|
3 |
||||||||
сто (2.4) |
можно записать |
|
|
|
|
||||
√ |
|
|
̂ |
I2s = т2(T)/3, |
|
|
|
||
т. е. в этом случае в (2.1) |
|
I3s |
|
||||||
̂ |
|
. |
|||||||
|
|
|
|
|
|
не учитывается влияние |
|
||
Эксперименты показывают, что условие (2.4) |
достаточно хо- |
||||||||
|
̂ |
||||||||
рошо выполняется для большой группы материалов (металлов, некоторых видов пластмасс и др.). Ему можно дать энергетическую интерпретацию. Если объемную плотность (e) потенциальной энергии упругой деформации представить через главные напряжения, то получим
(e) = 21 + 22 + 23 − 2 ( 1 2 + 2 3 + 3 1),
2E
18 |
Условие текучести |
где — коэффициент Пуассона; E — продольный модуль упругости. Вычитая отсюда объемную плотность
V(e) = 1 −6E2 ( 1 + 2 + 3)2
энергии, связанной с изменением объема, находим объемную плотность потенциальной энергии формоизменения
(e) |
= (1 + ) |
( 1 − 2)2 + ( 2 − 3)2 + ( 3 − 1)2 |
. |
F |
|
6E |
|
Сравнивая это равенство с (2.4), получаем условие текучести в виде
3E (e) |
= т2. |
|
F |
||
1 + |
||
|
Эта интерпретация хорошо согласуется с представлениями о микромеханизме пластической деформации, связанном со скольжением по определенным плоскостям в твердом кристаллическом теле. Такой процесс приводит к изменению формы в окрестности рассматриваемой точки и объясняет для (2.4) название энергетического условия текучести.
Если ввести интенсивность напряжений |
|
|
|
|||||||
|
и |
√ |
|
|
|
|
|
|
|
|
|
|
− |
|
2 |
− |
|
|
|
||
|
|
= |
( 1 |
|
2)2 |
+ ( 2 − 3)2 + ( 3 |
|
1)2 |
, |
(2.5) |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
||||
значение которой при одноосном растяжении напряжением совпадает со значением этого напряжения, то (2.4) примет вид
и = т(T).
Для материалов, обладающих свойством деформационной анизотропии, предложено достаточно большое число условий текучести, которые представляют собой обобщения условий (2.2)– (2.4) или их комбинации.
При продолжении процесса нагружения за пределом текучести у конструкционных материалов, как правило, увеличивается сопротивляемость пластическому деформированию. Для материалов с выраженным пределом текучести упрочнение связано
Условие текучести |
19 |
с изменением как размеров, так и положения начальной поверхности текучести в пространстве напряжений. Последующие поверхности текучести, которые образуются в процессе нагружения и отделяют области упругих и пластических деформаций друг от друга, называют поверхностями нагружения. Соотношение, определяющее характер изменения начальной поверхности текучести в зависимости от текущего напряженного состояния и предыстории деформирования, называют условием упрочнения. В случае изотропного упрочнения поверхность нагружения однородно расширяется, сохраняя свою форму, и в простейшем виде может быть описана функцией нагружения
f( ij) = т( ,T), |
(2.6) |
где — скалярный внутренний параметр состояния, называемый параметром упрочнения. В процессе пластического деформирования его значение возрастает.
Параметр упрочнения можно определить различными способами. Один из них заключается в его приравнивании достигну-
той интенсивности деформации сдвига 2 |
I2e, где I2e — второй |
|||
инвариант девиатора деформации e, |
другой — в его приравни- |
|||
√ |
̂ |
̂ |
||
ij d"ij(p), где |
̂ |
|
|
|
вании диссипации энергии при пластическом деформировании |
||||
∫ |
"ij(p) = "ij − "ij(e) − "ij(T) |
|
|
|
— компоненты тензора пластической деформации, "(ije) и "(ijT) —
компоненты тензоров соответственно упругой и температурной деформации, а тензор " малой деформации с компонентами
"ij в данном случае принято называть тензором полной де- |
|||||
формации. Третий |
̂ |
|
|
|
|
|
способ связан с выбором в качестве меры |
||||
упрочнения накопленной пластической деформации |
|
||||
|
= ∫ √ |
|
|
|
(2.7) |
|
3 d"ij(p) d"ij(p), |
||||
|
|
2 |
|
|
|
называемой параметром Удквиста.
Если начальным считать состояние, при котором пластические деформации отсутствуют, и использовать условие (2.4), то
20 |
Условие текучести |
||
(2.6) можно записать в виде |
|
|
|
|
s s = 2 2 |
( ,T), |
|
|
ij ij |
т |
|
где правая часть равенства определяет изменение предела текучести при чистом сдвиге, обусловленное изотропным упрочнением и температурой. Так как условия изотропного упрочнения не учитывают эффект Баушингера, наличие которого подтверждено экспериментально, то они пригодны лишь для приближенного описания пластического деформирования изотропных материалов со сравнительно малым параметром упрочнения, когда влияние этого эффекта не очень существенно.
Пример 2.1. В случае слабовыраженного упрочнения материала условие пластичности можно принять в виде равенства касательного октаэдрического напряжения N и напряжения текучести при чистом сдвиге т, т. е. N = т или и = т. Последнее соотношение в развернутом виде выглядит следующим образом:
1 |
|
|
|
||
√( 11 − 22)2 +( 22 − 33)2 +( 33 − 11)2 +6( 122 + 232 + 312 ) = |
|||||
√ |
|
||||
2 |
|||||
|
|
|
= т. (2.8) |
||
#
Пример 2.2. Для плоского напряженного состояния условие пластичности (2.8) примет вид
112 + 222 − 11 22 + 3 122 = т2, |
|
|
||||
а для плоского деформированного состояния при 33 = |
1 |
( 11 + 22) |
||||
2 |
||||||
получим |
|
|
||||
|
|
|
||||
( 11 − 22)2 + 4 122 = (√3 т) |
2 |
|
|
|||
. |
|
|
||||
2 |
|
|
|
|
||
|
|
|
|
|
|
|
Сопоставим последнее условие с условием текучести по теории наибольшего касательного напряжения. Последнее имеет вид
max = 12√( 11 − 22)2 + 4 212 = т.
Условие текучести |
21 |
Видно, что эти условия совпадают с точностью до постоянного
1 |
|
|
множителя, а если положить т = √ |
|
т, то совпадение будет пол- |
3 |
||
ным. С другой стороны, если принять т = 12 т, что соответствует теории наибольших касательных напряжений, то правые части
сравниваемых условий текучести будут отличаться в |
2 |
|
≈ 1,15 |
|
√ |
|
|
||
3 |
||||
раза. # |
|
|
|
|
Пример 2.3. Условие текучести (2.8) можно записать в терминах главных напряжений. Легко установить, что для двух частных случаев, когда 1 = 2 и 2 = 3, условие пластичности (2.8) записывают одинаково: 1 − 3 = т. #
Анизотропное упрочнение материала при фиксированной температуре и идеальном эффекте Баушингера, когда предел текучести при разгрузке уменьшается настолько, насколько он увеличился при предшествующем нагружении, можно описать параллельным перемещением начальной поверхности текучести
в пространстве напряжений, т. е. вместо (2.6) написать |
|
f( ij − ij) = т(T), |
(2.9) |
где ij — компоненты тензорного внутреннего параметра состояния ̂, называемого тензором трансляции и определяющего положение центра поверхности нагружения. Упрочнение такого вида называют трансляционным или кинематическим. Если пренебречь изменением объема при пластическом деформировании, то (2.9) примет вид
f(sij − ′ij) = т(T),
где ′ij = ij − kk ij/3 — компоненты девиатора ̂′ трансляции центра поверхности нагружения. В первом приближении
′ij = ĉ′(T)"(ijp),
где c ′(T) — коэффициент, характеризующий свойства данного
̂
материала.
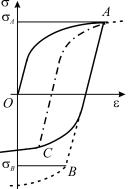
Пример 2.4. Пусть образец материала подвергнут одноосному растяжению (точка A на рис. 2.3). Если теперь провести
22 |
Условие текучести |
разгрузку и перейти к сжатию, то при изотропном упрочнении пластическое деформирование должно возобновиться после достижения точки B, ордината которой по абсолютному значению равна ординате точки A ( B = − A). В действительности пластическое деформирование при последующем сжатии обычно возобновляется при меньшем по абсолютному значению напряжении (кривая AC на рис. 2.3). Идеальный эффект Баушингера соответствует наличию только анизотропного упрочнения и приводит к повышению предела текучести при первоначальном растяжении и понижению его при последующем сжатии на одинаковую величину. Идеальный эффект Баушингера при нелинейном упрочнении описывает правило Мазинга, согласно которому кривая AC подобна кривой OA, но имеет удвоенный масштаб по осям абсцисс и ординат. Если в точке C снова провести разгрузку и перейти затем к растяжению, то в соответствии с принципом Мазинга кривая деформирования (штрих-пунктирная линия на рис. 2.3 должна пройти через точку A.
Рис. 2.3.
#
При кинематическом упрочнении первоначально изотропный материал становится анизотропным, причем пластическая деформация не зависит от среднего напряжения, а направления главных осей тензора напряжений не меняются. Так как условия
Условие текучести |
23 |
кинематического упрочнения описывают идеальный эффект Баушингера, то они применимы для сравнительно небольшого числа упрочняющихся материалов. В общем случае комбинированного упрочнения материала поверхность нагружения изменяет свои размеры и форму, перемещаясь в пространстве напряжений.
Вопросы и задачи
1.Что называют условием пластичности (условием текучести)?
2.Что называют кривой текучести и какими свойствами она обладает?
3.Напишите выражение, определяющее объемную плотность энергии формоизменения.
4.Приведите пример записи уравнения поверхности пластичности (поверхности текучести) для случаев изотропного упрочнения, кинематического упрочнения и комбинированного (изотропно-кинематического) упрочнения. Что называют поверхностью нагружения?
5.В координатах рис. 2.2 при условии sijsij = 2 т2(1 + 2) для аппроксимации примера 1.1 постройте изменение поверхности
нагружения при одноосном деформировании до "11 = "1 > "т, затем до −"1 и снова до "1 при трех вариантах :
= 2√I2̂e |
; = 2 т ∫ |
ij d"ij(p); = ∫ |
||
|
|
1 |
|
|
Выполнить то же самое, но при условии "11
√
2 (p) (p)
3d"ij d"ij .
= 2"22.
6.Что называют эффектом Баушингера, идеальным эффектом Баушингера ?
7.Сформулируйте правило Мазинга.
8.Как применить правило Мазинга для построения диаграммы с линейным упрочнением при знакопеременном деформировании?
9. При c ′ = const постройте траекторию трансляции центра
̂
поверхности нагружения при деформировании как в задаче 5. Выполните то же самое, но при условии "11 = 2"22.