Геомеханика / лекции Геомеханика / Лекция 13 Приближённые методы

8

Лекция 13.

1 час.

ПРИБЛИЖЁННЫЕ МЕТОДЫ ВЫЧИСЛЕНИЯ ПАРАМЕТРОВ НАПРЯЖЁННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ГОРНЫХ ПОРОД ВОКРУГ СИСТЕМЫ ВЫРАБОТОК

В практике горного дела очень важно иметь представление о распределении напряжений в массивах пород при сложных сочетаниях выработок, целиков, выработанного пространства и дневной поверхности. В таких случаях рассмотренные методы уже не являются эффективными и потому были разработаны другие подходы.

Если для одиночных выработок решение бигармонического уравнения может быть получено с применением функций комплексных переменных и конформного отображения односвязных областей, то для системы выработок и целиков, т. е. в случае, характерном для условий очистных выработок, весьма эффективными оказываются так называемые численные методы.

Основным достоинством этих методов является универсальность, применимость для широкого класса случаев и относительная простота вычислений. Их недостатком является большой объем вычислений, однако применение электронно-вычислительной техники позволяет его преодолеть и при достаточной надежности исходных данных обеспечить точность решений, достаточную для практики.

При этом необходимо учесть, что если аналитические методы позволяют получить параметры напряженно-деформированного состояния среды во всех её точках, то при использовании численных методов эти параметры получают для отдельных контрольных точек, а затем с помощью подходящих интерполирующих функций распространяют полученные решения на остальные точки рассчитываемой области.

Основная идея численных методов решения дифференциальных уравнений заключается в замене частных производных функции F какими-либо более простыми выражениями.

В частности, одним из подобных численных методов является метод конечных разностей или метод сеток. Общий принцип этого метода состоит в том, что расчётная область покрывается регулярной сеткой, а дифференциальное уравнение для какой-либо точки заменяется некоторым уравнением в конечных разностях, Это уравнение получают путем замены в дифференциальном уравнении производных и других дифференциальных операций их приближенными выражениями через разностные отношения или значения функций в узлах сетки, окружающих расчётную точку (рис.13.1).

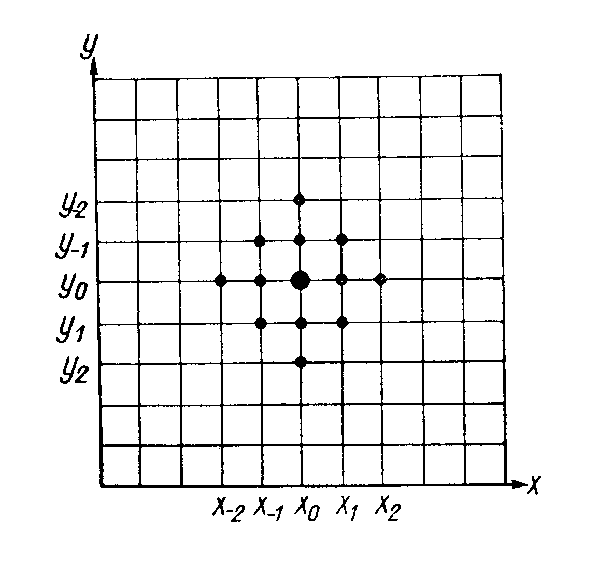
Рис. 13.1. Схема расположения узлов сетки, входящих в приближённое уравнение, при замене бигармонического уравнения уравнением в конечных разностях.

В результате решение дифференциального уравнения сводится к решению системы алгебраических линейных уравнений.

Поскольку метод конечных разностей является лишь приемом решения дифференциальных уравнений, ему в полной мере свойственны недостатки, присущие определению напряженно-деформированного состояния массива пород методами плоской теории упругости. К ним прежде всего относятся сложность аппроксимации граничных условий, в частности, при наличии угловых точек на контуре исследуемой области, а также весьма малая возможность учета неоднородности массива пород, что имеет особо важное значение для исследования систем выработок, где необходимо рассматривать значительные по размерам области массива горных пород, включающих различные геологические структуры и структурные неоднородности низких порядков.

С точки зрения этих недостатков более перспективны численные методы, основанные на положениях строительной механики - вариационно-разностные методы и метод конечных элементов, базирующиеся на энергетических принципах теории упругости. В определённом смысле эти методы можно рассматривать как развитие методов сеток и перехода к нерегулярному разбиению расчётных областей на отдельные элементы.

При вариационно-разностном методе используют широко известное положение теории упругости о том, что полная потенциальная энергия деформируемой системы может быть определена как разность между работой внешних нагрузок и внутренних сил (энергии деформации):

П = П_у - А, (13.2)

где П_у — энергия упругого деформирования; А — работа внешних нагрузок.

При этом минимальное значение потенциальной энергии соответствует состоянию устойчивого равновесия.

Энергию упругого деформирования и работу внешних нагрузок выражают через компоненты тензора деформаций и перемещений. Искомыми перемещениями и и v являются те значения, которые приводят выражение полной потенциальной энергии к минимуму.

Для нахождения перемещений и и v рассматриваемую область расчета S покрывают сеткой, разбивающей ее в большинстве случаев на треугольные ячейки (рис. 13.2б).

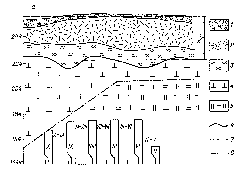
Рис. 13.2. Геологический разрез рудной залежи (а) и его схема с разбивкой на элементарные ячейки (б) для расчета напряженно-деформированного состояния пород вокруг очистных камер и в целиках вариационно-разностным методом (рудник “Ковдор”, Ковдорское флогопитовое месторождение, Кольский полуостров).

1—наносы; 2—вермикулитовая порода; 3 — гидрофлогопитовая руда; 4— оливиниты; 5 — флогопит; 6—верхняя граница части массива, выделенной для расчетов; 7—усредненные границы толщи покрывающих пород над участком массива, выделенным для расчетов; 8 — контакт пород, учитываемый в расчетах.

X. IX, . . ., V—очистные камеры;. X—IX, IX—VIII, .... VI—V—межкамерные целики.

Контур области аппроксимируют конечным числом прямолинейных отрезков, причем напряжения, деформации и массовые силы считают линейно распределенными по площади ячеек, а компоненты вектора смещений относят к узлам сетки.

В конечном итоге получают систему из 2n (плоский случай) и 3n (объёмный случай) линейных алгебраических уравнений (n - число узлов) относительно и_i и v_i, в которой вид свободных членов зависит от граничных условий и от массовых сил. По найденным значениям и_i и v_i вычисляют компоненты тензора напряжений в отдельных точках рассматриваемой области.

Поскольку выражения для потенциальной энергии П_i в каждой ячейке составляют независимо от других ячеек, а затем все значения П_i суммируют и минимизируют по всем неизвестным и_i и v_i, значения упругих постоянных G_i и v_i (где G_i - модуль сдвига; v_i - коэффициент Пуассона) в соседних ячейках могут быть различными, что открывает неограниченные возможности для учета неоднородности свойств массива. Это обусловило успешное применение данного метода для оценки напряженно-деформированного состояния пород вокруг горных выработок, пройденных в существенно неоднородных (слоистых) массивах.

На рис. 13.3 показаны результаты вычислений компонент тензора напряжений и перемещений вокруг камер и целиков в массиве пород Ковдорского флогопитового месторождения (Кольский полуостров).

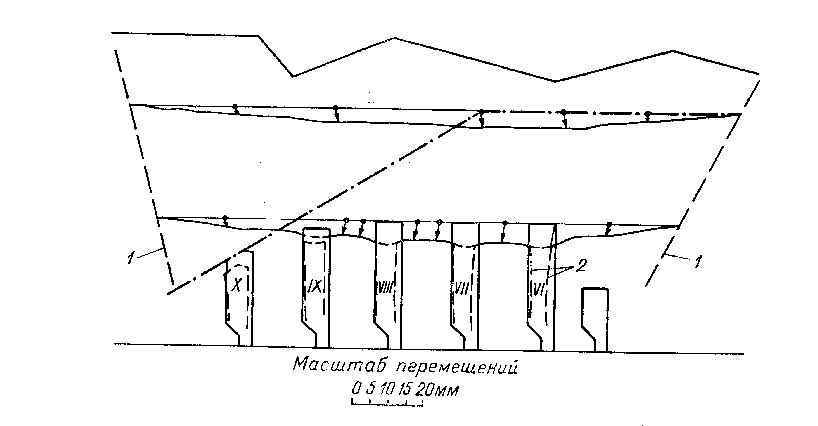
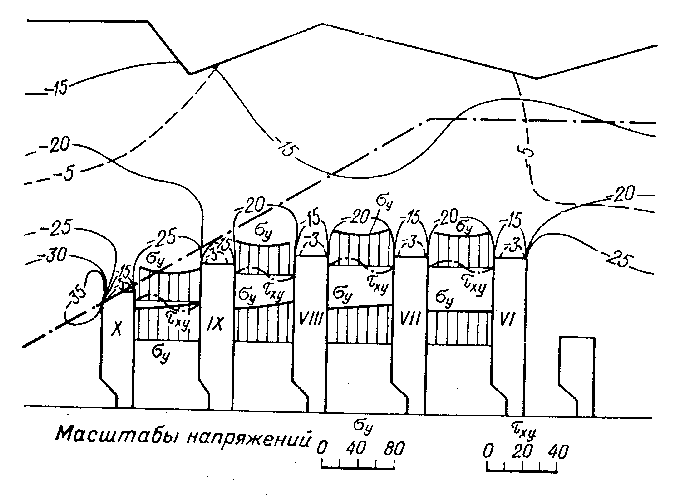
Рис. 13.3. Изолинии главных напряжений s₃ (сплошная), s₁ (штриховая) и эпюры напряжений s_у и t_ху (а), а также эпюры перемещений (б) в массиве пород вокруг камер и целиков (рудник “Ковдор”, Кольский полуостров).

1 - границы области деформирования; 2 - контуры сечений камер после деформирования.

Метод конечных элементов также является вариационным методом, но, в отличие от вариационно-разностного метода, в его основу положен принцип возможного изменения сил в узлах. Условию совместности деформаций отвечает минимум дополнительной работы, которая получается как произведение сил на перемещения узлов (принцип Кастельяно).

Достоинствами метода конечных элементов являются:

• простота получения конечных решений;

• возможность сгущения сети элементов в ожидаемых местах высоких градиентов исследуемого параметра (напряжений или деформаций);

• возможности задания граничных условий в перемещениях или усилиях по какому-либо закону их распространения;

• принципиальная возможность задания в любом элементе модели упругих констант среды, моделирования любой последовательности образования отработанных пространств и схем нагружения модели и т.д.

При применении метода конечных элементов область, напряженно-деформированное состояние которой необходимо определить, представляется в виде совокупности дискретных элементов - плоских или пространственных элементов типа стержневых или рамных конструкций. При этом, в отличие от метода конечных разностей, соблюдается ясная физическая трактовка решаемых задач. Вместе с тем необходимость определения свойств каждого элемента в отдельности дает возможность учитывать неоднородность свойств деформируемой области, а также рассчитывать области сколь угодно сложной конфигурации, без принципиальных изменений путей решения. В частности, метод конечных элементов успешно применяют для расчетов напряженного состояния плотин, откосов и их оснований.

Метод конечных элементов позволяет оперировать с элементами различной формы. Однако, для практических задач наиболее удобными оказались треугольные элементы, позволяющие легко оконтуривать расчётные области и сгущать сетку в местах ожидаемых концентраций напряжений или деформаций.

При этом конечному элементу приписываются следующие свойства:

• перемещения u и v, линейно зависящие от координат в пределах элемента, изменяются линейно вдоль любой прямой линии в элементе, т.е. прямые отрезки в недеформируемом элементе - в том числе и стороны элемента - остаются прямыми и после деформирования;

• деформации и напряжения линейно распределены по площади элемента и записываются относительно его центра тяжести.

Условие сплошности удовлетворяется тем, что в процессе деформирования элементы не теряют контакта друг с другом в узловых точках.

В методе конечных элементов предполагается, что все силы, действующие на тело, приложены в узлах, т. е. силовые взаимодействия между элементами осуществляются только в узловых точках. Например, деформирование элемента от формы 1 до формы 2 (рис.13.4) обусловлено приложением со стороны соседних элементов (или внешних воздействий) узловых сил F_i, F_j и F_k, каждая из которых раскладывается на соответствующие составляющие по координатным осям.

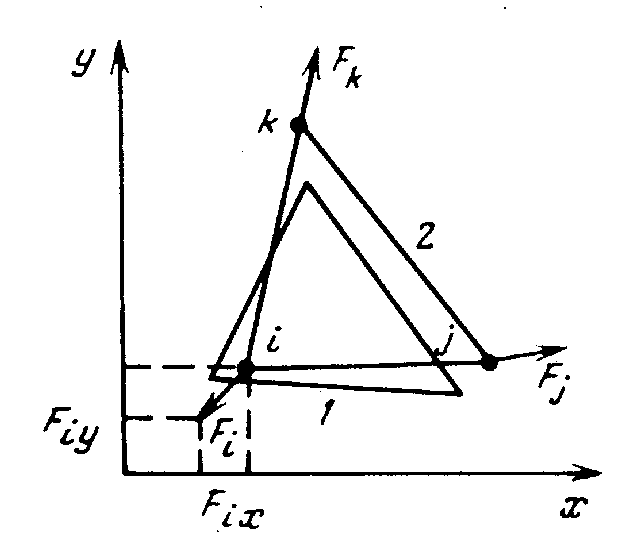
Рис.13.4. Схема деформирования элемента узловыми силами.

Для вывода зависимостей компонентов узловых сил от компонентов узловых перемещений используется принцип равенства работы узловых сил работе внутренних напряжений при бесконечно малых возможных перемещениях.

В конечном итоге, для всей расчётной области получают систему линейных уравнений, в которых выражены взаимосвязи между известными узловыми силами и неизвестными узловыми перемещениями.

На рис. 13.4 приведён пример расчёта величин напряжений методом конечных элементов для системы нескольких камер и целиков.

Рис. 13.4. Результаты расчёта величин напряжений методом конечных элементов для системы нескольких камер и целиков.

Метод конечных элементов практически без всяких изменений может быть применён и для моделей дискретных сред. С этой целью в обычную программу метода конечных элементов вводятся специальные контактные элементы, в частности, рассмотренные нами ранее элементы Гудмана-Беста, с соответствующими свойствами на контактах этих элементов.

К настоящему времени значительные успехи достигнуты в применении метода конечных элементов и для решения задач в нелинейной постановке, в частности для упруго-пластических и вязко-пластических сред, а также для сред, не сопротивляющихся растяжению, и для сред с отдельными трещинами.

Современные программы метода конечных элементов представляют собой уже не просто метод расчёта напряжений, а по существу аппарат математического моделирования процессов, протекающих в исследуемых объектах. В частности, применительно к процессам геомеханики в этих программах величины вычисляемых напряжений автоматически проверяются на соответствие условиям равновесия и неразрывности в случае сплошной среды или другим условиям для дискретных моделей, они также автоматически сопоставляются с прочностными параметрами среды. Таким образом, инженеру уже нет нужды самому анализировать поля напряжений, да и информация о них становится излишней. Совершенные программные системы позволяют обеспечить не только получение практически конечной информацией о состоянии тех или иных участков расчётной области в соответствующем графическом виде, но и предоставить пользователю ряд рекомендаций по отбору технических мероприятий для обеспечения устойчивого состояния выработок или снижению риска возникновения опасных проявлений горного давления.