Черник, О. В. Контрольная тетрадь по теории вероятностей и математической статистике

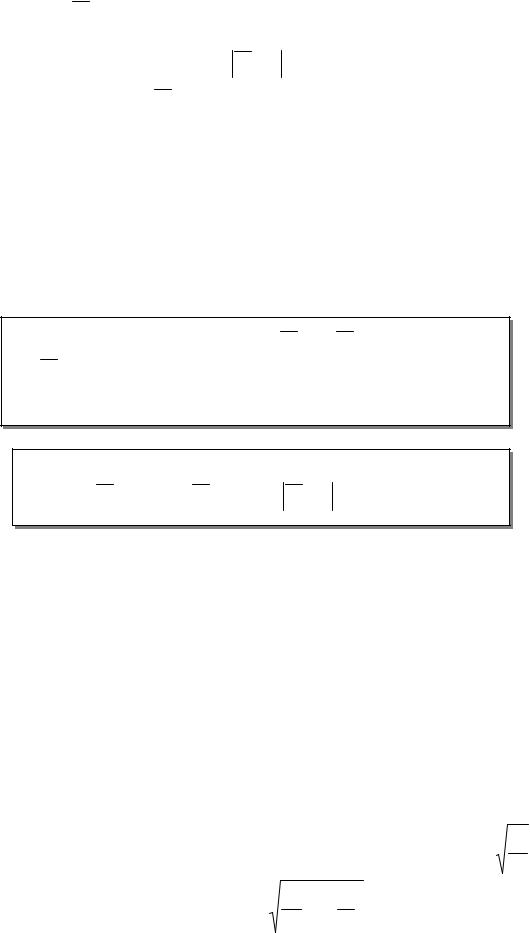
Оценка θn называется состоятельной, если при неограниченном увеличении объема выборки n оценка стремится по вероятности к

оцениваемому параметру, т.е. lim P(θn −θ < ε) =1 для любых ε > 0 .

n→∞

Несмещенная оценка θn параметра θ называется эффективной, если

она имеет наименьшую дисперсию среди всех возможных несмещенных оценок параметра θ .

Однако точечная оценка является лишь приближенным значением неизвестного параметра, даже если она несмещенна и состоятельна, и для выборки малого объема может существенно отличаться от самого параметра.

Поэтому, чтобы получить представление о точности и надежности оценки, рассматривают интервальную оценку параметра, т.е. такой

доверительный интервал, который с заданной надежностью

(доверительной вероятностью) покроет неизвестное значение параметра.

Доверительный интервал: (θn − ∆; θn + ∆),

где θn – точечная оценка неизвестного параметра θ , ∆ – точность оценки.

Надежность оценки (доверительная вероятность):

P(θn − ∆ <θ <θn + ∆)= P(θn −θ < ∆) = γ .

Доверительный интервал для генеральной средней M ( X ) , найденный

по выборке большого объема

Чтобы составить доверительный интервал, который с заданной

надежностью

γ покрывает генеральную

среднюю

M ( X ) , используют

формулу:

M ( X ) (x −tσ

; x +tσ

),

x

x

где параметр t

находят из равенства Φ(t) =

γ

, применяя таблицу значений

2

интегральной функции Лапласа (см. приложение 2);

σ

– средняя квадратичная ошибка выборки для

x

. В случае повторной

x

выборки или,

если объем генеральной

совокупности

N очень

велик

по

сравнению с объемом выборки n , то

σ

находят по формуле σ

=

s2

. А

x

x

n

для случая бесповторной выборки – σ

s2

n

=

1−

.

x

n

N

33

Доверительный интервал для генеральной доли p , найденный по

выборке большого объема

Чтобы составить доверительный интервал, который с заданной надежностью γ покрывает генеральную долю p , используют формулу:

p (ω −tσω; ω, +tσω ),

где параметр t находят из равенства Φ(t) = γ2 , применяя таблицу значений

интегральной функции Лапласа (см. приложение 2); σω – средняя квадратичная ошибка выборки для ω . В случае повторной

выборки или,			если объем генеральной					совокупности N очень		велик	по
сравнению с			объемом			выборки n ,		то σω находят	по	формуле
σω	=	ω(1−ω)	.		А	для	случая	бесповторной	выборки		–
		n
σω	=	ω(1−ω)		−	n
		n	1		.
					N

C помощью формул, рассмотренных в параграфе «Статистические оценки», решаются задачи трех типов.

I тип.

Даны: надежность γ , объем выборки n и точечная оценка – выборочная

средняя x или выборочная доля ω (если точечная оценка не дана в условии задачи, то ее следует найти по вариационному ряду).

Найти: точность оценки ∆ или границы доверительного интервала.

Решение. 1) По заданной величине γ из равенства Φ(t) = γ2 , применяя

таблицу значений интегральной функции Лапласа (см. приложение 2), находим аргумент t ;

2) вычисляем среднюю квадратичную ошибку выборки σx или σω , учитывая тип выборки (повторная или бесповторная), используя формулы на с. 31–32;

3)находим точность оценки по формуле ∆ = tσx или ∆ = tσω ;

4)определяем доверительные границы (x − ∆; x + ∆)или (ω −∆;ω +∆). II тип.

Даны: ∆, n , x (или ω ).

Найти: надежность выборочной оценки γ .

Решение. 1) Вычисляем среднюю квадратичную ошибку выборки σx или σω , учитывая тип выборки (повторная или бесповторная), используя формулы на с. 31–32;

34

2) находим параметр t по формулам: t =	∆			или	t =	∆	;
	σ					σω
		x

3) для найденного значения t определяем значение функции Φ(t) по таблицам (см. приложение 2); γ = 2Φ(t).

III тип.

	Даны: γ , ∆,		(или ω ).
		x
	Найти: необходимый объем выборки n .					γ , применяя
	Решение. 1) По заданной величине γ				из равенства Φ(t) =
						2
	таблицу значений интегральной функции Лапласа (см. приложение 2),
	находим аргумент t ;							t2s2
	2) вычисляем			объем повторной	выборки по формуле		n ≈
									или
								2
	n ≈ t2ω(1−ω) .							∆
				Эти формулы можно использовать и		для	бесповторной
	∆2

выборки, если объем генеральной совокупности N не дан, но из условия задачи выясняется, что он значительно превосходит n . В общем случае,

объем бесповторной выборки n′ находим по формуле n′ = nnN+ N , где n –

объем повторной выборки при той же ∆ и γ .

35

ЗАДАНИЯ КОНТРОЛЬНОЙ РАБОТЫ

I.1. На пяти карточках написаны буквы А, Д, К, Л, О. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность того, что получится слово «КЛАД»?

2.Среди 18 студентов группы, из которых 9 девушек, разыгрывается 5 билетов. Какова вероятность того, что среди обладателей билетов окажутся 3 девушки?

3.Лифт в пятиэтажном доме отправляется с тремя пассажирами. Найти вероятность того, что все они выйдут на разных этажах, предполагая, что возможные способы распределения пассажиров по этажам равновероятны.

4.Десять студентов условились ехать определенным электропоездом, но не договорились о вагоне. Какова вероятность того, что ни один из них не встретится с другим, если в составе электропоезда 10 вагонов? Предполагается, что все возможности распределения студентов по вагонам равновероятны.

5.У сборщика 10 деталей, мало отличающихся друг от друга. Из них четыре первого, по две второго, третьего и четвертого видов. Какова вероятность того, что среди шести взятых одновременно деталей три окажутся первого вида, две второго и одна третьего?

6.Среди 30 одинаковых по внешнему виду тетрадей 18 в клетку. Наудачу взяли 6 тетрадей. Найти вероятность того, что из них хотя бы одна тетрадь в клетку.

7.Жеребьевкой 16 волейбольных команд разбиты на две подгруппы по 8 команд в каждой. Найти вероятность того, что 2 наиболее сильные команды окажутся в одной подгруппе.

8, Числа натурального ряда 1, 2, 3, 4, …, 10 расставлены в случайном порядке. Найти вероятность того, что числа 1, 2, 3 расположены рядом и притом в порядке убывания.

9.Группа из 10 мужчин и 10 женщин делится случайно на две равные подгруппы. Найти вероятность того, что в каждой подгруппе мужчин и женщин окажется поровну.

10.К празднику для детей приготовили 30 подарков трех видов: мягкие игрушки, конструкторы и книжки – в количественном соотношении 3:2:5 соответственно. Подарки упаковали по одному в одинаковые коробки. Найти вероятность того, что в трех наудачу выбранных коробках окажутся подарки разного вида.

11.На шести карточках написаны буквы А, С, К, В, О, М. После тщательного перемешивания берут по одной карточке и кладут последовательно рядом. Какова вероятность того, что получится слово «МОСКВА»?

12.Студент знает 20 из 30 вопросов программы экзамена. Чтобы сдать экзамен, необходимо ответить хотя бы на два из трех предложенных в билете вопросов. Найти вероятность сдачи экзамена.

13.Экзаменационный билет содержит два вопроса. Сколько вопросов из общего числа, равного 35, следует подготовить студенту, чтобы с

36

вероятностью 0,9 на экзамене можно было ожидать билет с обоими подготовленными вопросами?

14.Определить вероятность того, что четырехзначный номер первой встретившейся автомашины не содержит одинаковых цифр.

15.Бросают две игральные кости. Какова вероятность появления хотя бы одной шестерки?

16.В районе имеется 12 заводов, из которых три нерентабельных. На проверку случайным образом отобрано 2 завода. Найти вероятность того, что среди них хотя бы один нерентабельный.

17.В магазине имеются 30 телевизоров, причем 20 из них импортных. Найти вероятность того, что среди 5 проданных в течение дня телевизоров окажутся 3 импортных телевизора, предполагая, что вероятность покупки телевизоров разных марок одинакова.

18.Найти вероятность того, что наудачу выбранное двузначное число окажется кратным или 2, или 5.

19.Из 20 АЗС 8 расположены за чертой города. Для исследования рентабельности случайным образом отобрано 5 АЗС. Какова вероятность того, что среди отобранных окажется три АЗС в черте города?

20.Некто забыл последние две цифры телефонного номера, но помнит, что они нечетные и различные. Какова вероятность того, что он сразу наберет нужный номер, если будет набирать эти цифра случайно?

II. Варианты 1–10. В район поставляют продукцию три фирмы в отношении n1 : n2 : n3 . В продукции первой фирмы m1 % стандартных

изделий, второй – m2 %, третьей – m3 %. Найти вероятность того, что а)

приобретенное изделие окажется нестандартным; б) приобретенное качественное изделие поступило от i-го поставщика.

Вариант	1	2	3	4	5	6	7	8	9	10
n1	1	4	1	2	6	3	6	4	3	3
n2	2	5	3	4	8	5	8	6	7	2
n3	3	6	4	6	1	7	9	9	9	5
m1	90	80	70	60	75	88	95	97	72	90
m2	60	70	80	90	90	91	85	79	84	87
m3	80	60	90	70	85	79	76	86	96	75
i	1	2	3	1	2	3	1	2	3	1

Варианты 11–20. По результатам проверки контрольной работы

оказалось, что	в первой группе получили положительную оценку
m1студентов из	n1 , а во второй группе m2 из n2 . Найти вероятность того,

что: а) наудачу выбранная работа оценена положительно; б) наудачу выбранная работа, имеющая положительную оценку, написана студентом i-ой группы.

37

Вариант	11	12	13	14	15	16	17	18	19	20
m1	20	12	14	24	15	18	16	15	17	18
n1	30	24	28	35	25	30	24	30	34	27
m2	15	16	18	17	14	20	17	20	18	15
n2	25	32	30	28	26	32	28	32	28	26
i	1	2	1	2	1	2	1	2	1	2

III. Варианты 1–10. В среднем p % семей города пользуются услугами одного банка. Найти вероятность того, что:

1)из n1 случайно выбранных семей услугами данного банка пользуются m семей;

2)из n2 случайно выбранных семей услугами данного банка пользуются:

а) k семей; б) не менее k1 и не более k2 семей.
						6
Вариант	1	2	3	4	5		7	8	9	10
p	10	12	15	25	20	22	14	18	30	24
n1	9	6	8	5	7	6	4	5	3	9
m	3	2	4	3	2	3	1	4	2	5
n2	200	240	250	390	600	320	300	350	700	500
k	30	25	35	90	100	80	45	50	200	150
k1	25	20	30	80	90	70	35	40	190	140
k2	50	30	40	100	110	90	55	60	210	160

Варианты 11-20. Вероятность поражения вирусным заболеванием куста смородины равна p . Найти вероятность того, что:

1)из n1 кустов смородины зараженных вирусом окажется m кустов:

2)из n2 кустов смородины зараженных вирусом окажется: а) k кустов; б) не менее k1 и не более k2 кустов.

Вариант	11	12	13	14	15	16	17	18	19	20
p	0,1	0,12	0,15	0,25	0,2	0,22	0,14	0,18	0,3	0,24
n1	4	5	6	8	7	5	4	6	8	9
m	2	3	4	2	4	4	1	5	6	4
n2	300	400	500	600	750	800	200	250	100	150
k	27	45	70	145	155	160	25	40	35	40
k1	20	40	60	140	130	150	20	35	20	30
k2	40	50	80	160	160	180	30	50	40	50

38

IV. Пакеты акций могут принести доход владельцу с вероятностью p (для

каждого пакета). Владелец имеет n пакетов акций. Требуется: а) составить закон распределения случайной величиныX , выражающей число пакетов акций, по которым владелец может получить доход; б)

определить вид закона распределения случайной величины X ; в) построить многоугольник распределения; г) составить функцию распределения вероятностей случайной величины и построить ее график; д) найти числовые характеристики.

Вариант	1	2	3	4	5	6	7	8	9	10
p	0,12	0,21	0,32	0,44	0,56	0,15	0,24	0,33	0,48	0,55
n	3	3	3	3	3	4	4	4	4	4
						16
Вариант	11	12	13	14	15		17	18	19	20
p	0,1	0,2	0,3	0,4	0,5	0,1	0,2	0,3	0,4	0,5
n	5	5	5	5	5	6	6	6	6	6

V. Варианты 1-10. Случайная величина X задана интегральной функцией распределения вероятностей F(x). Требуется: а) построить график F(x); б) составить плотность распределения вероятностей f (x) и

построить ее график; в) найти числовые характеристики X ; г) вычислить
P(X < a); P(X > b); P(c < X < d`).
		0 при x < 0			a = 0.5; b = 0.6; c = 1 ; d =	3
1. F(x)= x2 при 0 ≤ x ≤1,							;
					3	4
1 при x >1
0 при x < 0
			2
2. F (x)=		x		при0 ≤ x ≤ 4,	a =1; b = 2; c = 2,5; d = 3;
		16
		1 при x > 4
0 при x < 0
			2
3. F(x)=		x		при0 ≤ x ≤ 6,	a = 3; b = 4; c = 2; d = 7;
		36
		1 при x > 6
0 при x < 0
			2
4. F(x)=	x			при0 ≤ x ≤ 5,	a = 2; b = 4; c =1,5; d = 5;
		25
		1 при x > 5

39

	0 при x < 0
			x	3
	5. F(x)=					при0 ≤ x ≤ 3,
			27
			1 при x > 3
	0 при x < 0
				2
	6. F(x)=	x				при0 ≤ x ≤ 3,
			9
			1 при x > 3

0 при x < 2

7.F(x)= x −2 при 2 ≤ x ≤ 3,1 при x > 3

0 при x < 3

8.F(x)= x −3 при3 ≤ x ≤ 4,1 при x > 4

0 при x < 0

9. F(x)= x при0 ≤ x ≤ 4,4 >

1 при x 4

0 при x < 0

10. F(x)= x при0 ≤ x ≤ 6,

6 >1 при x 6

a = 0,5; b =1; c = 2; d = 4;

a =1; b =1,5; c = 0,6; d =1,4;

a = 2,5; b = 3; c = 2,1; d = 4;

a = 3,5; b = 4; c = 3,1; d =5;

a =1; b = 3; c = 2; d =5;

a = 2; b =1; c = 4; d = 6.

Варианты 11-20. Случайная величина X имеет нормальный закон распределения с параметрами а и σ. Требуется: а) составить функцию распределения вероятностей F(x) и плотности вероятностей f (x), построить график f (x); б) найти вероятность попадания случайной величины X в интервал (α; β); в) вычислить вероятность того, что случайная величина X отклонится от своего математического ожидания не больше чем на δ; г) с помощью правила «3σ» определить диапазон изменения значений случайной величины X .

Вариант	11	12	13	14	15	16	17	18	19	20
а	20	500	140	230	54	320	440	74	650	90
σ	2	10	24	18	7	30	25	9	35	10
α	14	450	130	200	35	190	450	50	570	85
β	21	490	155	240	45	300	470	60	660	115
δ	4	20	32	27	13	64	50	12	56	16

40

VI. (Варианты 1–4) В мастерскую по ремонту и обслуживанию бытовой радиоэлектроники по схеме бесповторной выборки отобрано 50 рабочих дней прошедшего года и получены следующие данные о числе вызовов в день:

	Число
	вызовов в	5-10	10-15	15-20	20-25	25-30
	день
	Количество	6	13	18	10	3
	дней

Найти: 1. Найти числовые характеристики x и s2 вариационного ряда исследуемого признака и построить его гистограмму.

2. Определить: а) границы, в которых с вероятностью γ1 заключено среднее

число вызовов в день за предыдущий год; б) вероятность того, что доля дней в предыдущем году, в которых число вызовов было более m , отличается от выборочной доли таких вызовов не более чем на ∆ (по абсолютной величине); в) объем бесповторной выборки, при котором те же границы для среднего числа вызовов в день можно гарантировать с вероятностью γ2 .

Вариант		1		2		3	4
γ1		0,95		0,94		0,93	0,92
m		20		15		25	10
∆		0,1		0,11		0,09	0,08
γ2		0,9901		0,9911		0,9875	0,9886
Варианты 5–8
Коробки конфет		упаковываются		автоматически.		По схеме	бесповторной

выборки отобрано 130 из 2000 упаковок и получены следующие данные об их весе:

	Вес	950-975	975-1000	1000-1025	1025-1050	1050-1075
	упаковки
	Количество	6	38	44	34	8
	упаковок

Найти: 1. Найти числовые характеристики x и s2 вариационного ряда исследуемого признака и построить его гистограмму.

2. Определить: а) границы, в которых с вероятностью γ1 заключен средней

вес упаковок; б) вероятность того, что доля упаковок, вес которых менее m г, во всей партии отличается от выборочной доли таких упаковок не более чем на ∆ (по абсолютной величине); в) объем бесповторной выборки, при котором те же границы для среднего веса упаковок можно гарантировать с вероятностью γ2 .

Вариант	5	6	7	8
γ1	0,9901	0,9729	0,9651	0,9606
m	1000	1025	975	1050
∆	0,05	0,03	0,02	0,01
γ2	0,95	0,94	0,92	0,98

41

Варианты 9–12

По схеме бесповторной выборки в некотором крупном городе проводилось исследование количества вызовов скорой помощи в сутки. За последние три года отобрано 90 дней. Результаты представлены в таблице:

	Число вызовов	300-	400-	500-	600-	700-	800-	900-
		400	500	600	700	800	900	1000
	Количество	9	12	21	20	18	8	2
	дней

Найти: 1. Найти числовые характеристики x и s2 вариационного ряда исследуемого признака и построить его гистограмму.

2. Определить: а) вероятность того, что среднее число вызовов в день за указанный период отличается от среднего их количества в выборке не более чем на ∆ (по абсолютной величине); б) границы, в которых с вероятностью γ1 заключена доля тех дней из рассматриваемого периода, в которых

количество вызовов было не менее m ; в) объем бесповторной выборки, при котором те же границы для указанной доли можно гарантировать с вероятностью γ2 .

Вариант	9	10	11	12
∆	25	30	27	20
γ1	0,95	0,94	0,93	0,92
m	700	600	800	500
γ2	0,9876	0,9729	0,9651	0,9606

Варианты 13-16

По схеме бесповторной выборки в некотором промышленном регионе из 200 котельных обследовано 50. Получены следующие данные о числе дней, в течение которых котельные обеспечены топливом:

Число дней	0-6	6-12	12-18	18-24	24-30	30-36
Количество котельных	6	8	14	12	7	3

Найти: 1. Найти числовые характеристики x и s2 вариационного ряда исследуемого признака и построить его гистограмму.

2. Определить: а) вероятность того, что среднее число дней, в течение которых котельные обеспечены топливом, во всем регионе отличается от среднего выборочного не более чем на ∆ дней (по абсолютной величине); б) границы, в которых с вероятностью γ1 заключена доля тех котельных во

всем регионе, которые обеспечены топливом менее чем на m дней; в) объем бесповторной выборки, при котором те же границы для указанной доли можно гарантировать с вероятностью γ2 .

Вариант	13	14	15	16
∆	2	1	2,5	1,5
γ1	0,95	0,94	0,93	0,92
m	12	18	24	6
γ2	0,9876	0,9729	0,9651	0,9606

42