§ 5 ПОСТРОЕНИЯ С ПОМОЩЬЮ ДРУГИХ ИНСТРУМЕНТОВ 173

одного циркуля — не проводя самого отрезка. Вот решение этой задачи. Опишем окружность радиусом AB с центром B и на нем, отправляясь от A, как раньше, отмерим последовательно три дуги радиусом AB. Последняя точка C будет лежать

на прямой AB, причем мы бу-

дем иметь: AB = BC. Затем опи-

шем окружность радиуса AB с

центром A и построим точку C0,

обратную точке C относитель-

но этой окружности. Тогда полу-	A	C
		B
чим:			C
AC0 · AC = AB2,
AC0 · 2AB = AB2,
2AC0 = AB.
Значит, C0 есть искомая середина
отрезка.	Рис. 44. Нахождение середины отрезка
Другое построение с помо-

щью одного циркуля, также использующее обратные точки, заключается в нахождении центра данной окружности, когда начерчена только сама окружность, а центр неизвестен. Берем про-

извольную	точку P	на окружности и около нее как центра
			описываем круг произвольного радиу-
	S		са, пересекающийся с данным кругом в
			точках R и S. Из этих последних то-
	Q		чек как центров описываем дуги ради-
P			усом RP = SP , пересекающиеся, кроме
			точки P , еще в точке Q. Сравнивая то,
	Q
			что получилось, с рис. 41, мы видим,
R			что неизвестный центр Q0 есть точка,
			обратная точке Q относительно окруж-
Рис. 45. Нахождение		центра	ности с центром P , и Q0 может быть, как
			мы видели, построена с помощью одного
циркуля.	круга

§5. Построения с помощью других инструментов. Построения Маскерони с помощью одного циркуля

*1. Классическая конструкция, служащая для удвоения куба. Мы рассматривали до сих пор только проблемы геометрических построений без использования иных инструментов, кроме циркуля и линейки. Если допускаются и другие инструменты, то, разумеется, разнообра-

174		ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ			гл. III
V		N		S
					Q
	U			D	T
		E
			y
		f
			B
		a	x
		G		A	M
	Z			R
	P				W
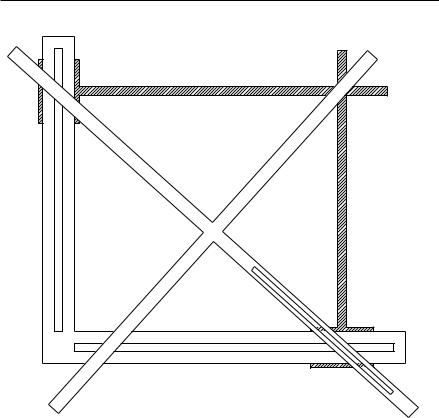
		Рис. 46. Инструмент, служащий для удвоения куба

зие возможных построений сильно увеличивается. Следующий пример может служить образцом того, как греки решали проблему удвоения куба. Рассмотрим (рис. 46) жесткий прямой угол MZN и подвижной прямоугольный крест V W , P Q. Двум дополнительным стержням RS и T U предоставлена возможность скользить, оставаясь перпендикулярными к сторонам прямого угла. На кресте пусть выбраны фиксированные точки E и G, причем расстояния GB = a и BE = f заданы. Располагая крест таким образом, чтобы точки E и G соответственно лежали на NZ и MZ, и перемещая стержни T U и RS, можно весь аппарат привести в такое положение, чтобы лучевые перекладины креста BW , BQ, BV проходили через вершины A, D, E прямоугольника ADEZ. Указанное на чертеже расположение всегда возможно при условии f > a. Мы видим сразу, что a : x = x : y = y : f, откуда, в частности, если положено f = 2a, получается x3 = 2a3. Значит, x есть ребро куба, объем которого вдвое больше, чем объем куба с ребром a. Таким образом, поставленная задача

§ 5 ПОСТРОЕНИЯ С ПОМОЩЬЮ ДРУГИХ ИНСТРУМЕНТОВ 175

решена.

2. Построения с помощью одного циркуля. Если вполне естественно, что с допущением большего разнообразия инструментов оказывается возможным решать более обширное множество задач на построение, то можно было бы предвидеть, что, напротив, при ограничениях, налагаемых на инструменты, класс разрешимых задач будет суживаться. Тем более замечательным нужно считать открытие, сделанное итальянцем Маскерони (1750–1800): все геометрические построения, выполнимые с помощью циркуля и линейки, могут быть выполнены с помощью одного только циркуля. Следует, конечно, оговорить, что провести на самом деле прямую линию через две данные точки без линейки невозможно, так что это основное построение не покрывается теорией Маскерони. Вместо того приходится считать, что прямая задана, если заданы две ее точки. Но с помощью одного лишь циркуля удается найти точку пересечения двух прямых, заданных таким образом, или точку пересечения прямой с окружностью.

Вероятно, простейшим примером построения Маскерони является удвоение данного отрезка AB. Решение было уже дано на стр. 166. Далее, на стр. 167 мы научились делить данный отрезок пополам. Посмотрим теперь, как разделить пополам дугу окружности AB с центром O.

	Вот
	описание этого построения (рис. 47).
	Радиусом AO проводим две дуги с		R
	центрами A и B. От точки O откла-
	дываем на этих дугах две такие ду-
	ги OP и OQ, что OP = OQ = AB. За-
	тем находим точку R пересечения ду-
	ги с центром P и радиусом P B и дуги	A		B
	с центром Q и радиусом QA. Наконец,
	взяв в качестве радиуса отрезок OR,	P	O	Q
	опишем дугу с центром P или Q до
	пересечения с дугой AB — точка пе-	Рис. 47. Нахождение середины ду-
	ресечения и является искомой сред-
			ги без линейки
	ней точкой дуги AB. Доказательство
	предоставляем читателю в качестве упражнения.

Было бы невозможно доказать основное утверждение Маскерони, указывая для каждого построения, выполнимого с помощью циркуля и линейки, как его можно выполнить с помощью одного циркуля: ведь возможных построений бесчисленное множество. Но мы достигнем той же цели, если установим, что каждое из следующих основных построений выполнимо с помощью одного циркуля:

1. Провести окружность, если заданы центр и радиус.

176

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

гл. III

2.Найти точки пересечения двух окружностей.

3.Найти точки пересечения прямой и окружности.

4.Найти точку пересечения двух прямых.

Любое геометрическое построение (в обычном смысле, с допущением циркуля и линейки) составляется из выполнения конечной последовательности этих элементарных построений. Что первые два из них выполнимы с помощью одного циркуля, ясно непосредственно. Более трудные построения 3 и 4 выполняются с использованием свойств инверсии, рассмотренных в предыдущем пункте.

		Q
		P
		B			B2
A	X	X
		O
			A	O	B
		C		C
					B1
Рис. 48. Пересечение окружности			Рис. 49. Пересечение окружно-
и	прямой, не проходящей через		сти и прямой, проходящей через
		центр		центр

Обратимся к построению 3: найдем точки пересечения данной окружности C с прямой, проходящей через данные точки A и B. Проведем дуги с центрами A и B и радиусами, соответственно равными AO и BO; кроме точки O, они пересекутся в точке P . Затем построим точку Q, обратную точке P относительно окружности C (см. построение, описанное на стр. 167). Наконец, проведем окружность с центром Q и радиусом QO (она непременно пересечется с C): ее точки пересечения X и X0 с окружностью C и будут искомыми. Для доказательства достаточно установить, что каждая из точек X и X0 находится на одинаковых расстояниях от O и P (что касается точек A и B, то аналогичное их свойство сразу вытекает из построения). Действительно, достаточно сослаться на то обстоятельство, что точка, обратная точке Q, отстоит от точек X и X0 на расстояние, равное радиусу окружности C (см. стр. 165). Стоит отметить, что окружность, проходящая через точки X, X0 и O, является обратной прямой AB в инверсии относительно круга C, так как эта окружность и прямая AB пересекаются с C в одних и тех же точках. (При инверсии точки основной окружности остаются неподвижными.)

Рис. 50. Пересечение двух прямых

§ 5 ПОСТРОЕНИЯ С ПОМОЩЬЮ ДРУГИХ ИНСТРУМЕНТОВ 177

Указанное построение невыполнимо только в том случае, если прямая AB проходит через центр C. Но тогда точки пересечения могут быть найдены посредством построения, описанного на стр. 169, как середины дуг C, получающихся, когда мы проводим произвольную окружность с центром B, пересекающуюся с C в точках B1 и B2.

Метод проведения окружности, обратной прямой, соединяющей две данные точки, немедленно дает и построение, решающее задачу 4. Пусть прямые даны точками A, B и A0, B0 (рис. 50). Проведем произвольную окружность C и с помощью указанного выше метода построим окружно-

сти,
обратные прямым AB и A0B0. Эти
окружности пересекаются в точке O
и еще в одной точке Y . Точка X, об-
ратная точке Y , и есть искомая точ-
ка пересечения: как ее построить —		A
уже было разъяснено выше. Что X
			O
есть искомая точка, это ясно из то-
го факта, что Y есть единственная
точка, обратная точке, одновременно	B	Y	C
принадлежащей обеим прямым AB
и A0B0; следовательно, точка X, об-
ратная Y , должна лежать одновре-	X	B
менно и на AB, и на A0B0.
			A
Этими двумя построениями за-

канчивается доказательство эквивалентности между построениями Мас-

керони, при которых разрешается пользоваться только циркулем, и обыкновенными геометрическими построениями с циркулем и линейкой.

Мы не заботились об изяществе решения отдельных проблем, нами здесь рассмотренных, так как нашей целью было выяснить внутренний смысл построений Маскерони. Но в каче-

Xстве примера мы еще укажем пятиугольни-

				ка; точнее говоря, речь идет о нахождении
		B	C	каких-то пяти точек на окружности, кото-
				рые могут служить вершинами правильно-
		F
	G		H	го вписанного пятиугольника.
				Пусть A — произвольная точка окруж-
	A	O	D	ности K. Так как сторона правильного
				вписанного шестиугольника равна радиусу
				круга, то не представит труда отложить
		Y		на K такие точки B, C, D, что ^ AB =

K^ BC = ^ CD = 60◦ (рис. 51). Проведем

дуги с центрами A и D радиусом, рав-

Рис. 51. Построение правильного пятиугольника

178

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

гл. III

ным AC; пусть они пересекаются в точ-

ке X. Тогда, если O есть центр K, дуга с

центром A и радиусом OX пересечет K в точке F , являющейся серединой дуги BC (см. стр. 169). Затем радиусом, равным радиусу K, опишем дуги с центром F , пересекающиеся с K в точках G и H. Пусть Y есть точка, расстояния которой от точек G и H равны OX и которая отделена от X центром O. В таком случае отрезок AY как раз и есть сторона искомого пятиугольника. Доказательство предоставляется читателю в качестве упражнения. Интересно отметить, что при построении используются только три различных радиуса.

В 1928 г. датский математик Ельмслев нашел в книжной лавке в Копенгагене экземпляр книги под названием Euclides Danicus, опубликованной в 1672 г. никому не известным автором Г. Мором. По титульному листу можно было сделать заключение, что это — просто один из вариантов евклидовых «Начал», снабженный, может быть, редакторским комментарием. Но при внимательном рассмотрении оказалось, что в ней содержится полное решение проблемы Маскерони, найденное задолго до Маскерони.

Упражнения. В дальнейшем дается описание построений Мора. Проверьте их правильность. Почему можно утверждать, что они решают проблему Маскерони?

1)К отрезку AB длины p восставите перпендикуляр BC. (Указание: продолжите AB до точки D таким образом, что AB = BD. Проведите произвольным радиусом дуги с центрами A и D и таким образом определите C.)

2)В плоскости даны как угодно расположенные отрезки длины p и q,

p

причем p > q. Постройте с помощью 1) отрезок длины x = p2 − q2.

√

3)По заданному отрезку a постройте отрезок a 2. (Указание: обратите

√√

внимание, что (a 2)2 = (a	3)2 − a2.)
4) По данным отрезкам p и q постройте отрезок x =									p2 + q2	. (Указание:
примите во внимание, что	x2 = 2p2	−	(p2	−	q2)	.)	Придумайте сами аналогич-
								p

ные построения.

5)Пользуясь предыдущими результатами, постройте отрезки p + q и p − q, предполагая, что отрезки длины p и q заданы как-то на плоскости.

6)Проверьте и постарайтесь обосновать следующее построение середины M данного отрезка AB длины a. На продолжении отрезка AB найдем такие точки C и D, что CA = AB = BD. Построим равносторонний треугольник ECD согласно условию EC = ED = 2a и определим M как пересечение окружностей с диаметрами EC и ED.

7)Найдите прямоугольную проекцию точки A на отрезок BC.

8)Найдите x по условию x : a = p : q, где a, p и q — данные отрезки.

9)Найдите x = ab, где a и b — данные отрезки.

Вдохновляясь результатами Маскерони, Якоб Штейнер (1796–1863) предпринял попытку исследования построений, выполнимых с помощью одной только линейки. Конечно, одна только линейка не выводит за

§ 5

ПОСТРОЕНИЯ С ПОМОЩЬЮ ДРУГИХ ИНСТРУМЕНТОВ

179

пределы данного числового поля, и потому она недостаточна для выполнения всех геометрических построений в классическом их понимании. Но тем более замечательны результаты, полученные Штейнером при введенном им ограничении — пользоваться циркулем только один раз. Он доказал, что все построения на плоскости, выполнимые с помощью циркуля и линейки, выполнимы также с помощью одной линейки при условии, что задан единственный неподвижный круг вместе с центром. Эти построения подразумевают применение проективных методов и будут описаны позднее (см. стр. 217).

* Без круга, и притом с центром, обойтись нельзя. Например, если дан круг, но не указан его центр, то найти центр с помощью одной линейки невозможно. Мы сейчас докажем это, ссылаясь, однако, на факт, который будет установлен позднее (см. стр. 240): существует такое преобразование плоскости самой в себя, что а) заданная окружность остается неподвижной, б) всякая прямая линия переходит в прямую, в) центр неподвижной окружности не остается неподвижным, а смещается. Само существование такого преобразования свидетельствует о невозможности построить центр данной окружности, пользуясь одной линейкой. В самом деле, какова бы ни была процедура построения, она сводится к ряду отдельных этапов, заключающихся в проведении прямых линий и нахождении их пересечений друг с другом или с данной окружностью. Представим себе теперь, что вся фигура в целом — окружность и все прямые, проведенные по линейке при выполнении построения центра — подвергнута преобразованию, существование которого мы здесь допустили. Тогда ясно, что фигура, полученная после преобразования, также удовлетворяла бы всем требованиям построения; но указываемое этой фигурой построение приводило бы к точке, отличной от центра данной окружности. Значит, построение, о котором идет речь, невозможно.

3. Черчение с помощью различных механических приспособлений. Механические кривые. Циклоиды. Изобретение различных механизмов, предназначенных для того, чтобы чертить различные кривые, помимо окружности и прямой линии, чрезвычайно расширяет область фигур, допускающих построение. Например, если имеется инструмент, позволяющий чертить гиперболы xy = k, и другой инструмент, вычерчивающий параболы y = ax2 + bx + c, то любая проблема, приводящая к кубическому уравнению

ax3 + bx2 + cx = k,

(1)

может быть решена конструктивно, с помощью только этих инструментов. В самом деле, решение уравнения (1) равносильно решению системы

xy = k, y = ax2 + bx + c;

(2)

точнее, корни уравнения (1) являются x-координатами точек пересечения гиперболы и параболы, представляемых уравнениями (2). Таким

180

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

гл. III

y

y

x

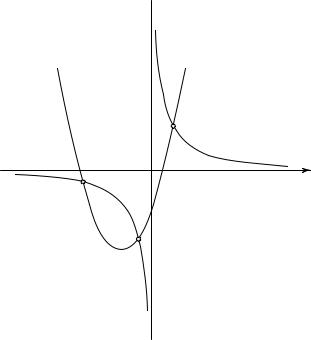
Рис. 52. Графическое решение кубического уравнения

образом, решения уравнения (1) допускают построение, если разрешается пользоваться инструментами, с помощью которых можно начертить кривые (2).

Уже математикам древности были известны многие интересные кривые, которые могут быть определены и начерчены с помощью простых механических приспособлений. Среди таких «механических» кривых особенно видное место занимают циклоиды. Птолемей (около 200 года до нашей эры), обнаруживая необычайную проницательность, сумел использовать эти кривые для описания планетных движений.

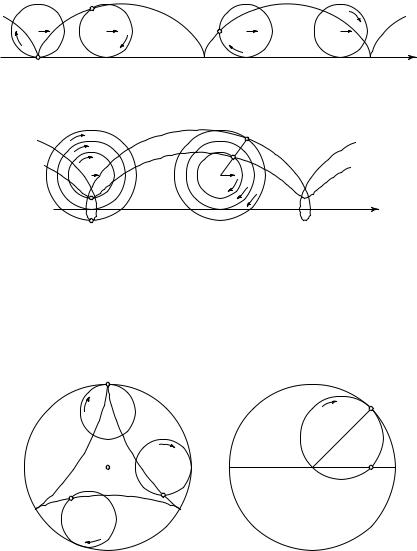
Циклоида самого простого вида представляет собой траекторию движения точки P , фиксированной на окружности диска, катящегося без скольжения по прямой линии. На рис. 53 изображены четыре положения точки P в различные моменты времени. По форме циклоида напоминает ряд арок, опирающихся на горизонтальную прямую.

Разновидности этой кривой получаются, если возьмем точку P или внутри диска (как на спице колеса), или на продолжении радиуса за пределы диска.

§ 5

ПОСТРОЕНИЯ С ПОМОЩЬЮ ДРУГИХ ИНСТРУМЕНТОВ

181

P2

P3

P4

P1

Рис. 53. Циклоида

Рис. 54. Циклоиды общего вида

Эти две кривые показаны на рис. 54.

Дальнейшие разновидности циклоиды возникают, когда наш диск катится не по прямой, а по дуге окружности. Если при этом катящийся диск с радиусом r остается все время касающимся изнутри той большой окружности C радиуса R, по которой он катится, то траектория точки, фиксированной на окружности диска, называется гипоциклоидой.

Рис. 55. Трехрогая гипоциклои-	Рис. 56. Прямолинейное дви-
да	жение при качении круга по
	кругу двойного радиуса

Когда диск прокатывается по всей окружности C ровно один раз, то точка P возвращается в исходное положение только в том случае, если радиус C является кратным радиуса c. На рис. 55 изображена замкнутая гипоциклоида, соответствующая предположению R = 3r. В более общем

182

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

гл. III

случае, если R = mn r, то гипоциклоида замкнется после того, как диск c

прокатится по окружности C ровно n раз, и будет состоять из m арок. Заслуживает особого упоминания случай R = 2r. Любая точка P на окружности диска будет описывать в этом случае один из диаметров большой окружности C (рис. 56). Предоставляем читателю доказать это в качестве задачи.

Еще один тип циклоид получается, когда диск c катится по окружности C, касаясь ее все время извне. Получающиеся при этом кривые носят название эпициклоид.

*4. Шарнирные механизмы. Инверсоры Поселье и Гарта.

Оставим на время в стороне вопрос о циклоидах (они появятся еще раз в этой книге — довольно неожиданно) и обратимся к иным методам механического воспроизведения кривых линий. Мы займемся сейчас

шарнирными механизмами.

Механизм этого типа представляет собой систему сочлененных между собой твердых стержней, обладающих такой степенью свободы, чтобы каждая его точка была способна описывать определенную кривую. Циркуль также является простейшим шарнирным механизмом, по существу состоящим из одного стержня с закрепленным концом.

Рис. 57. Преобразование прямолинейного движения во вращательное

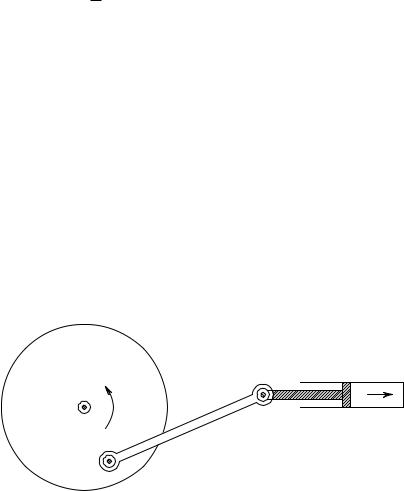
Шарнирные механизмы издавна находят себе применение как составные части машин. Одним из самых знаменитых (в историческом отношении) примеров является так называемый «параллелограмм Уатта». Это приспособление было изобретено Джемсом Уаттом при решении следующей проблемы: как связать поршень с точкой махового колеса таким образом, чтобы вращение колеса сообщало поршню прямолинейное движение? Решение, данное Уаттом, было лишь приближенным, и, несмотря на усилия многих первоклассных математиков, проблема конструирования механизма, сообщающего точке в точности прямолиней-

§ 5

ПОСТРОЕНИЯ С ПОМОЩЬЮ ДРУГИХ ИНСТРУМЕНТОВ

183

ное движение, долгое время оставалась нерешенной. Было даже сделано предположение, что такой механизм неосуществим: это было как раз тогда, когда всякого рода «доказательства невозможности» привлекли к себе всеобщее внимание. Тем большее изумление было вызвано в кругах математиков, когда французский морской офицер Поселье (в 1864 г.) все же изобрел несложный механизм, действительно разрешающий проблему в положительном смысле. В связи с введением в употребление хорошо действующих смазочных веществ техническая проблема потеряла свое значение для паровых машин.

S

P

O T Q

R

Рис. 58. Инверсор Поселье, преобразующий вращательное движение в прямолинейное

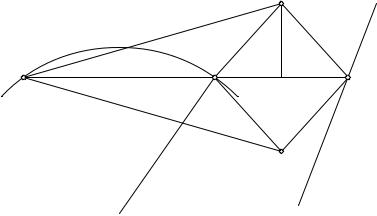
Назначение механизма Поселье заключается в том, чтобы превращать круговое движение в прямолинейное. В основе этого механизма лежит теория инверсии, изложенная в § 4. Как видно из рис. 58, механизм состоит из семи жестких стержней, два из них — длины t, четыре — длины s и один — произвольной длины. Точки O и R закреплены и расположены таким образом, что OR = P R. Весь аппарат может быть приведен в движение, будучи подчинен указанным условиям. Мы сейчас убедимся, что, когда точка P описывает дугу окружности с центром R и радиусом RP , точка Q описывает прямолинейный отрезок. Обозначая основание перпендикуляра, опущенного из точки S на прямую OP Q, через T , мы замечаем, что

OP · OQ = (OT − P T ) · (OT + P T ) = OT 2 − P T 2 =

= (OT 2 + ST 2) − (RT 2 + ST 2) = t2 − s2. (3)

Величина t2 − s2 постоянная; положим t2 − s2 = r2. Так как OP · OQ =

184

ГЕОМЕТРИЧЕСКИЕ ПОСТРОЕНИЯ

гл. III

r2, то точки P и Q взаимно обратные относительно окружности с центром O и радиусом r. В то время как P описывает дугу окружности, проходящей через O, Q описывает кривую, обратную этой дуге. Но кривая, обратная окружности, проходящей через O, есть, как мы видели, не что иное, как прямая линия. Итак, траектория точки Q есть прямая, и инверсор Поселье чертит эту прямую без линейки.

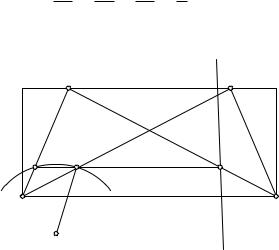
Другой механизм, решающий ту же проблему, есть инверсор Гарта. Он состоит всего лишь из пяти стержней, сочленение которых показано на рис. 59. Здесь AB = CD, BC = AD. Через O, P и Q обозначены точки, соответственно зафиксированные на стержнях AB, AD и CB, притом

таким образом, что OBAO = PAPD = QBCQ = mn . Точки O и S закреплены

на плоскости неподвижно, с соблюдением условия OS = P S. Больше связей нет, и механизм способен двигаться. Очевидно, прямая AC всегда

E	B	D	F
O	P	Q
A			C
	S
	Рис. 59. Инверсор Гарта

параллельна прямой BD. В таком случае точки O, P и Q лежат на одной прямой, и прямая OP параллельна прямой AC. Проведем перпендикуляры AE и CF к прямой BD. Мы имеем

AC · BD = EF · BD = (ED + EB) · (ED − EB) = ED2 − EB2.

Но 2ED

2

+ AE2 = AD2

и

EB2 + AE2 = AB2

. Значит,

ED2

−

EB2

=

2

. Далее,

AD − AB

OP

=

AO

=

m

и

OQ

=

OB

=

n

.

m + n

AC

AB

m + n

BD

AB

Следовательно,

OP · OQ =

mn

· BD · AC =

mn

· (AD

2

−

2

).

AB

(m + n)2

(m + n)2

Последняя полученная величина не изменяется при движении механизма. Поэтому точки P и Q являются взаимно обратными относительно