
Lektsii_TFKP
.pdfограничена на g r , а |
|
|
z - z0 |
|
= |
|
z - z0 |
|
<1. Следовательно, последнее равенство |
||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||
|
x - z0 |
|
|
r |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
можно почленно проинтегрировать на g r : |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
f (x )dx |
|
|
|
1 |
|
¥ |
f (x )dx |
|
¥ |
|
|||||||||
|
f (z) = |
|
ò |
|
= |
|
ò å |
(z - z0 )n = åcn (z - z0 )n , |
|||||||||||||||||||
|
x - z |
|
|
|
n+1 |
||||||||||||||||||||||
|
|
|
|
2ip g r |
|
|
2ip g r n=0 |
(x - z0 ) |
n=0 |
|
|||||||||||||||||
где cn = |
1 |
|
|
f (x )dx |
(n = 0,1, 2,...). ■ |
|
|
|
|
|
|
|
|
||||||||||||||
2ip |
ò (x - z |
0 |
|
)n+1 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
g r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Ряд (5.3), коэффициенты которого определены формулами (5.4), |
|||||||||||||||||||||||||||
называется рядом Тейлора функции f (z) |
с центром в точке z0 . |
|
|||||||||||||||||||||||||
Теорема (единственность разложения в степенной ряд). |
|
||||||||||||||||||||||||||
Если функция |
f (z) в круге U = |
{z, |
|
z - z0 |
|
< R} представима как сумма |
|||||||||||||||||||||
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
степенного |
ряда |
f (z) |
= åcn (z - z0 )n , |
|
то |
коэффициенты |
этого ряда |
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
однозначно определяются по формулам сn = |
f (n) (z0 ) |
(n = 0,1, 2,...). |
|||||||||||||||||||||||||
|
|
n! |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Доказательство следует из формулы (5.2).
Основные разложения:
|
¥ |
z |
n |
|
( |
|
|
|
< +¥); |
|
|
|
|
|
|
|||||||||||||
· |
ez = å |
|
|
|
|
z |
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
(5.5) |
n=0 |
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
(-1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
¥ |
|
n-1 |
z |
2n-1 |
( |
|
|
|
< +¥); |
||||||||||||||||||
· |
sin z = å |
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
(5.6) |
n=1 |
|
|
(2n -1)! |
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
(-1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
¥ |
|
|
n |
z |
2n |
( |
|
|
|
< +¥); |
||||||||||||||||
· |
cos z = å |
|
|
|
|
|
|
|
|
z |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
(5.7) |
n=0 (2n)! |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
¥ |
|
|
|
|
|
2n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
· |
sh z = nå=1 |
z |
|
( |
|
z |
|
< +¥); |
||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
(2n -1)! |
||||||||||||||||||||||||||||
(5.8) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
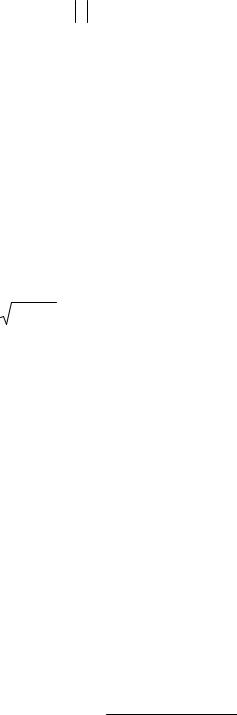
·
(5.9)
·
(5.10) (здесь ln z
·
¥ |
|
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ch z = nå=0 |
z |
|
( |
|
z |
|
< +¥); |
|
|
|
|
||||||
|
|
|
|||||||||||||||
(2n)! |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
ln(1+ z) |
¥ |
(-1) |
n-1 |
z |
n |
( |
|
|
|
< 1) |
|||||||
= å |
n |
|
|
z |
|
||||||||||||
|
|
|
|||||||||||||||
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
– главная ветвь логарифма);
¥
(1 + z)a = åCan zn (z < 1), Can
n=0
ìa(a -1)?
= ïí ï 1,
î
(a - n + 1), n =1,2,...
n!
n = 0
(5.11) (здесь za – главная ветвь степенной функции); в частности,
|
|
|
|
1 |
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
· |
|
|
|
|
= åzn ( |
|
|
z |
|
< 1). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
1 |
- z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
(5.12) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример |
5.3. Разложить |
|
указанные |
функции |
|
в |
|
ряд |
Тейлора в |
||||||||||||||||||||||||||||||||||||||||||||||||
окрестности точки |
z0 : a) |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
, |
z 0 = 0; |
b) |
1 |
|
|
|
, |
z 0 = 0; c) |
|
|
z |
|
, |
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
z 2 + 1 |
|
(1 - z)3 |
|
1 - z + z 2 |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
z 0 = 0; d) |
|
z -1 |
|
|
|
|
, z 0 = -1; |
|
e) |
|
cos z , |
|
z 0 |
|
= p |
; f) |
|
ez , |
z0 = 3; |
g) главная |
|||||||||||||||||||||||||||||||||||||
2z 2 + 5z + |
2 |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
ветвь функции ln(z + |
1 + z2 ), |
|
|
z 0 = 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
a) Из формулы (5.12) для |
|
|
z |
|
<1 имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
¥ |
|
|
|
n |
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= å(- z2 ) = |
å(-1)n z2n . |
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- (- z 2 ) |
|
|
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
z 2 +1 1 |
|
|
n=0 |
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
b) Из теоремы о почленном дифференцировании степенных рядов и |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
формулы (5.12) имеем для |
|
|
|
|
z |
|
|
<1: |
|
|
|
|
|
|
² |
|
|
|
|
|
|
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
1 |
|
|
1 |
æ |
1 |
|
|
ö |
² |
|
|
|
|
1 |
|
|
æ |
¥ |
|
n |
ö |
1 |
æ |
¥ |
n-1 |
ö |
|
1 |
|
¥ |
|
|
n-2 |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
ç |
|
|
÷ |
|
|
|
ån(n |
-1)z |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
= |
|
|
ç |
|
|
|
|
|
÷ |
= |
|
|
|
|
ç åz |
|
|
÷ |
= |
|
ç ånz |
|
|
|
÷ |
|
= |
|
|
|
|
. |
|
||||||||||||||||||
|
|
|
|
3 |
|
2 |
|
|
|
|
|
2 |
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
(1 - z) |
|
|
è1- z ø |
|
|
|
|
|
|
|
|
|
è n=0 |
|
|
|
ø |
|
è n=1 |
|
|
|
ø |
|
|
|
2 n=2 |
|
|
|
|
|
||||||||||||||||||||||||
c) Записав данную функцию в виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
= |
|
|
|
|
|
z (z + 1) |
|
|
|
= |
|
z(z + 1) |
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z + 1)(z 2 - z + 1) |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
1 - z + z 2 |
|
|
|
1 + z 3 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||

и воспользовавшись формулой (5.12), для всех z < 1 имеем:
z(z + 1) |
¥ |
|
||
= z(z + 1)å(-1)n z3n = z(z + 1)(1 - z3 + z6 - z9 + ? + (-1)n z3n + ? |
)= |
|||
1 + z 3 |
|
|||
n=0 |
|
|||
= z + z 2 - z 4 - z 5 + z 7 + z 8 - z 10 - z 11 + ... + (-1)n z 3n +1 + (-1)n z 3n + 2 + ...
d)Воспользовавшись методом неопределенных коэффициентов,
разложим функцию на простейшие дроби:
|
z -1 |
= |
z -1 |
= |
|
A |
|
|
+ |
|
|
B |
|
= |
|
A(2z + 1)+ B(z + 2) |
, |
||||||||
|
2z 2 + 5z + 2 |
(z + 2)(2z + 1) |
|
z + 2 |
2z + 1 |
|
|
|
(z + 2)(2z + 1) |
|
|||||||||||||||
|
|
|
z |
1 |
: 2A+ B = 1 |
ü |
|
|
|
A = 1, |
|
|
|
|
|
||||||||||
|
|
|
|
ï |
Þ |
|
|
|
|
|
|
||||||||||||||
|
|
|
z 0 :A+ 2B = -1 |
ý |
B = -1. |
|
|
|
|||||||||||||||||
|
|
|
ï |
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
þ |
|
|
|
|
|
|
|
|
|
|
|
|
||
Получаем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z -1 |
|
= |
|
|
|
1 |
|
- |
1 |
|
|
. |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
z + |
|
2z +1 |
|
|
||||||||||
|
|
|
|
2z 2 + 5z + 2 |
|
|
2 |
|
|
|
|
||||||||||||||
Применяя к каждой из дробей формулу (5.12), получаем:
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
= å(-1)n (z + 1)n , |
|
z +1 |
|
< 1, |
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
z + 2 |
1 |
- (- (z + 1)) |
|
||||||||||||||||||||||
|
|
|
|
|
|
n=0 |
¥ |
|
|
|
|
|
|
|
|
|
1 . |
|||||||||||||
|
1 |
|
|
|
|
|
|
1 |
|
|
|
|
|
|
1 |
|
2n (z + 1)n , |
|
|
|
|
|||||||||
|
= |
|
|
|
|
|
= - |
|
|
|
|
= - å |
|
z +1 |
|
< |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2z + 1 |
2 |
(z + 1)-1 |
1 - 2(z + 1) |
|||||||||||||||||||||||||
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
2 |
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
Отсюда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
z -1 |
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
¥ |
|
|
¥ |
|
|
|
|
|
|
|
|||
|
|
|
|
|
= å(-1)n (z + 1)n + å2n (z + 1)n = å(2n + (-1)n )(z + 1)n |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
2z 2 + 5z + 2 |
n=0 |
|
|
|
|
|
|
n=0 |
|
n=0 |
|
||||||||||||||||||

для всех точек круга |
|
z +1 |
|
|
< |
|
1 |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
e) Пользуясь тригонометрическими формулами, получаем: |
|
|
|
|
|||||||||||||||||||||||||||||||||||||
cos z = cosææ z - p |
ö |
+ p ö= cosæ z - p |
öcosp - sinæ z - p ösin p |
= |
|
||||||||||||||||||||||||||||||||||||
|
|
|
çç |
|
|
4 |
÷ |
|
|
|
|
4 |
÷ |
|
|
|
ç |
4 |
÷ |
|
|
|
|
|
4 |
|
ç |
|
÷ |
4 |
|
|
|
||||||||
|
|
|
èè |
|
|
ø |
|
|
|
|
ø |
|
|
|
è |
ø |
|
|
|
|
|
|
è |
|
4 ø |
|
|
|
|||||||||||||
|
|
|
= |
|
2 |
|
é |
|
|
|
|
æ |
|
|
|
p ö |
æ |
|
|
|
|
p öù |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
2 |
|
|
ê cosç z - |
|
÷ - sinç z - |
÷ú . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
è |
|
|
|
4 ø |
|
|
è |
|
|
|
|
4 øû |
|
|
|
|
|
|
|
|
|
||||||
Из разложений (5.6) и (5.7): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
¥ (- |
|
|
n æ |
|
|
- |
p |
ö |
2n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n-1æ |
p |
ö |
2n-1 |
|
||||||||||
æ |
p ö |
|
1) |
|
ç z |
|
|
4 |
÷ |
|
|
æ |
|
|
|
|
p |
ö |
¥ |
|
(-1) |
ç z - |
4 |
÷ |
|
|
|||||||||||||||
|
å |
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
|
|
|
|
= å |
|
|
|
|
è |
ø |
|
|
|||||||||||||
cosç z - |
÷ |
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
, |
sinç z |
- |
|
|
|
÷ |
|
|
|
|
|
|
|
|
. |
||||||
|
|
|
|
|
|
(2n)! |
|
|
|
|
|
|
|
|
|
|
|
(2n -1)! |
|
|
|||||||||||||||||||||
è |
4 ø |
|
n=0 |
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
4 |
ø |
n=1 |
|
|
|
|
|
|
|||||||||||||
Окончательно имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
é |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
p ö2 |
æ |
|
|
|
p ö3 |
æ |
p ö4 |
|
|
|
|
||||||||||
|
|
2 ê |
|
|
æ |
|
|
|
|
p ö |
|
|
ç z |
- |
4 ÷ |
|
|
|
ç z - 4 ÷ |
|
|
ç z - 4 ÷ |
|
|
|
|
|||||||||||||||
cos z = |
|
ê1 + |
|
|
ç z - |
|
|
÷ |
- |
è |
|
ø |
|
- |
è |
|
|
|
ø |
|
|
+ |
è |
ø |
+ ... |
|
|||||||||||||||
2 |
|
|
|
|
|
2! |
|
|
|
|
3! |
|
|
|
4! |
|
|||||||||||||||||||||||||
|
|
ê |
|
|
è |
|
|
|
|
|
4 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
ê |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ë |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
p |
|
ö2n-1 |
|
|
æ |
|
|
|
|
p |
ö2n+2 |
ù |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
ç z - |
|
|
|
|
÷ |
|
|
|
|
|
|
|
ç z - |
|
|
÷ |
|
ú |
|
|
|
|
|
||||||||||||
... + (-1)n-1 |
è |
|
|
4 |
ø |
|
|
|
|
+ |
(-1)n |
è |
|
|
|
|
4 |
ø |
|
+ ...ú , |
z ÎC . |
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
(2n + 2)! |
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
(2n +1)! |
|
|
|
|
|
|
|
ú |
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ú |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
û |
|
|
|
|
|
||
f) Из разложения (5.5) имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ez =e(z -3)+3 = e3 å(z |
- 3) |
|
, z ÎC . |
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
n! |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
g) Продифференцируем функцию ln(z +  1 + z2 ):
1 + z2 ):
F(z) = (ln (z + |
¢ |
= |
1 |
é |
+ |
z |
ù |
= |
1 |
. |
1 + z2 )) |
z + 1 + z2 |
×ê1 |
1 + z2 |
ú |
|
|||||
|
|
|
ë |
|
û 1 + z2 |
|
||||
Из формулы (5.11) имеем:

(1 + t)-1/ 2
Тогда
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
(1 + t)-1/ 2 = åC-k1/ 2tk ( |
|
t |
|
<1), |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
ì |
k 1×3×? ×(2k -1) |
|
|
|
|
|
|
|
|
|
|
|||||||||
k |
(-1) |
|
|
|
|
|
|
|
, k =1,2,...; |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||||||||
ï |
|
k! 2k |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
C-1/ 2 |
=í |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
ï |
1 |
|
|
|
|
|
, k =0. |
|
|
|||||||||||
|
î |
|
|
|
|
|
|
|
|||||||||||||
¥ |
|
1×3 |
×? × (2k -1) |
|
|
|
|
|
|
¥ |
|
|
|
|
|
(2k)! |
|
||||
=1+ å(-1)k |
tk = |
å(-1)k |
tk . |
||||||||||||||||||
|
|
22k (k!)2 |
|||||||||||||||||||
k =1 |
|
|
k! 2k |
|
|
|
|
k =0 |
|
|
|
|
|
|
|||||||
|
|
|
¥ |
|
(2k)! |
|
|
|
|
|
|
|
|
|
|
|
|
||||
(1 + z2 )-1/ 2 = å(-1)k |
|
|
|
|
z2k |
( |
|
z |
|
<1). |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||
22k (k!)2 |
|
|
|||||||||||||||||||
|
|
|
k =0 |
|
|
|
|
|
|
|
|
|
|||||||||
Проинтегрировав почленно последнее равенство, получим:
|
|
2 |
z |
¥ |
k |
|
(2k)! z2k +1 |
|
||||
ln(z + |
1 + z |
|
)= òF(t)dt = å(-1) |
|
|
|
|
|
|
, |
||
|
2 |
2k |
2 |
|
2k + 1 |
|||||||
|
|
|
0 |
k =0 |
|
|
(k!) |
|
|
|||
где z < 1.

§5.3. Ряд Лорана
Теорема (о разложении в ряд Лорана).
Любую функцию f (z) , аналитическую в кольце V = {z,r < z - z0 < R}, 0 £ r < R £ ¥ , можно в этом кольце представить как сумму сходящегося ряда
|
|
|
|
|
|
¥ |
|
|
|
|
|
f (z) = åcn (z - z0 )n , |
|
|
|
|
|
|
|
n=-¥ |
|
|
|
|
|
|
(5.13) |
коэффициенты которого определяются по формулам |
|
|
||||
сn = ò |
|
f (x )dx |
(n = 0,±1,±2,...), |
|||
|
|
|||||
|
n+1 |
|||||
|
x - z0 |
|
= r (x - z0 ) |
(5.14) |
||
|
|
|||||
|
|
|
|
|
|
|
где r < r < R .
|
|
|
|
|
|
Доказательство. |
|
|
Фиксируем |
точку |
z ÎV |
и |
|
построим |
|
|
|
|
|
|
кольцо |
||||||||||||||||||||||||||||||||||||||||||||||
V |
¢ |
= {x : r |
¢ |
< |
|
x - z0 |
|
|
|
¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
¢ |
, V |
¢ |
Ì V . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
< R } такое, что z ÎV |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
По |
|
|
|
интегральной |
|
|
|
формуле |
|
|
|
|
Коши, |
|
|
|
f (z) = |
1 |
|
|
|
|
ò |
|
f (x )dx |
= |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2ip |
|
|
x - z |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
f (x )dx |
|
|
|
|
|
|
f (x )dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¶V ¢ |
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
1 |
|
|
, где G |
¢ |
= {x : |
|
x - z0 |
|
¢ |
|
¢ |
= |
{x |
|
|
|
x -z0 |
|
¢ |
|
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
: |
|
|
|||||||||||||||||||||||||||||||||
|
2ip |
ò |
|
|
x - z |
|
2ip ò |
x - z |
|
|
|
|
|
= R }, g |
|
|
|
= r |
} – |
||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
G¢ |
|
|
|
|
|
|
|
|
|
|
|
|
g ¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
окружности, ориентированные против часовой стрелки. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
При |
|
|
любых |
x ÎG |
¢ |
|
|
|
справедливы |
|
соотношения |
|
|
z - z0 |
|
|
< 1 |
|
и |
||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x - z0 |
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
(z - z0 )n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
å |
|
|
|
|
|
|
(сходимость равномерная на G¢ по |
||||||||||||||||||||||||||||||||||
x - z |
|
|
|
|
|
|
|
|
æ |
|
|
z - z0 |
ö |
|
(x - z0 )n+1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
- |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
(x - z0 )ç1 |
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
x - z0 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f (x )dx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
f (x )dx |
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
(n = 0,1,2...). |
||||||||||||||||||||||
x ), поэтому |
|
|
|
|
|
|
= |
åcn (z - z0 )n , |
|
|
cn = |
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
2ip Gò¢ x - z |
|
|
|
|
2ip Gò¢ (x - z0 )n+1 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
При |
|
|
|
всех |
|
x Îg |
¢ |
|
|
|
|
справедливы |
|
|
|
|
соотношения |
|
x - z0 |
|
|
|
|
< 1 |
|
и |
|||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z - z0 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
¥ |
|
(x - z0 )n-1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
- |
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= å |
|
|
|
|
|
|
|
|
|
|
|
(сходимость |
||||||||||||||||
x - z |
z - z0 - (x - z |
0 ) |
|
|
|
|
|
|
æ |
|
x - z0 |
|
|
ö |
|
(z - z0 )n |
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(z - z0 )ç1- |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
z - z0 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
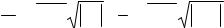
|
|
|
|
|
|
|
¢ |
|
|
|
|
1 |
|
|
f (x )dx |
¥ |
d |
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
равномерная |
|
на g |
по |
x ), |
поэтому |
- 2ip gò¢ |
x - z |
|
= nå=1 (z - z0 )n |
, |
||||||||||
|
|
|
||||||||||||||||||
dn = |
1 |
ò |
f (x )(x - z0 )n-1 dx |
(n =1, 2...). |
|
|
|
|
|
|
|
|
|
|
||||||
2ip |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
g ¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В |
последних |
|
двух |
формулах заменим |
n |
на |
- n , получим |
||||||||||||
сn = d-n |
= |
1 |
|
|
f (x )(x - z0 )-n-1 dx |
(n = -1, - 2,...). |
|
|
|
|
|
|
|
|
||||||
2ip |
ò |
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
g ¢ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
Таким |
образом, |
f (z) = åcn (z - z0 )n , |
где |
|
ряд определяется как |
||||||||||||||
n=-¥
объединение двух рядов (по положительным и неположительным степеням),
а окружности |
G¢ |
и |
|
|
g ¢ |
можно заменить (по интегральной теореме Коши) |
||||||||||||||||||||||||||||||
любой окружностью |
|
x - z0 |
|
|
= r , r < r < R . ■ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
Ряд (5.13), коэффициенты которого определяются по формулам (5.14), |
||||||||||||||||||||||||||||||||
называется рядом Лорана функции |
f (z) в кольце V . |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение åcn (z - z0 )n называется правильной частью ряда Лорана, |
||||||||||||||||||||||||||||||||
|
|
-1 |
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
c-1 |
|
|
|
c-2 |
|
|
|
c-3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
а |
|
å cn (z - z0 )n |
= |
|
+ |
|
|
|
+ |
|
|
|
|
+ ... |
|
|
– главной частью ряда |
|||||||||||||||||||
|
z |
|
- z0 |
|
|
(z - z0 )2 |
|
|
(z - z0 )3 |
|
|
|
||||||||||||||||||||||||
|
n=-¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Лорана. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
Замечание. Если |
z0 = ¥ , то рядом Лорана в окрестности бесконечно |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
||
удаленной точки функции |
|
|
f (z) называется ряд |
f (z) = |
åcn zn , при этом |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=-¥ |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
~ |
(z) = c0 |
+ |
|
c |
-1 |
+ |
|
c |
-2 |
+ |
|
c |
-3 |
+ ..., а главной |
||||
правильной его частью называется |
|
f1 |
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
z |
|
|
|
|
|
|
|||||||||||||||||||||||||||
|
~ |
(z) = c z + c |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z2 |
|
z3 |
||||||||
– |
|
z2 + c |
|
z3 |
+ .... |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
f |
2 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
По формуле Коши – Адамара, |
1 |
|
= lim n |
|
cn |
, |
1 |
= lim n c-n . |
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
R |
|
n®¥ |
|
|
|
|
|
|
r |
|
|
n®¥ |
|
|
|
|
|
|
|
|
|
Теорема (о единственности разложения в ряд Лорана). |
||||||||||||||||||||||||||||||||
z - z0 |
Всякий сходящийся ряд по отрицательным и положительным степеням |
|||||||||||||||||||||||||||||||||||
является рядом Лорана своей суммы, т.е. если функция f (z) в кольце |
||||||||||||||||||||||||||||||||||||
V представима рядом вида (5.13), то коэффициенты этого ряда определяются по формулам (5.14).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|||||||
Пример 5.4. Разложить в ряд Лорана функцию f (z) = |
|
в |
|||||||||||||||||||||
z2 - 3z + 2 |
|||||||||||||||||||||||
кольце: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a) V1 = {z : 0 < |
|
z |
|
< 1}; b) V2 = {z :1 < |
|
z |
|
< 2}; c) V3 = {z : 2 < |
|
z |
|
< ¥}. |
|
||||||||||
|
|
|
|
|
|
|
|||||||||||||||||
Решение. Используя метод неопределенных коэффициентов, |
|||||||||||||||||||||||
представим |
рациональную функцию |
f (z) в виде суммы простых дробей: |
|||||||||||||||||||||
1 |
1 |
|
|
1 |
1 |
|
|
|
|
|
|
|
|||||||||||
f (z) = |
|
= |
|
= |
|
- |
|
. |
|
||||||||||||||
z2 - 3z + 2 |
(z -1)(z - 2) |
z - 2 |
z -1 |
|
|||||||||||||||||||
Пользуясь формулой (5.12), получаем следующие разложения:
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
a) - |
|
|
|
|
= |
|
|
|
|
|
|
|
|
|
|
= |
|
å zn |
(сходится при |
|
z |
|
< 1), |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
z -1 |
|
|
1 |
- z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
|
|
|
¥ æ z ön |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
|
|
1 |
|
|
|
= - |
|
1 |
× |
|
|
|
1 |
|
|
|
|
|
|
= - |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
< 2 ), поэтому в |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
|
÷ |
|
|
|
(сходится |
|
при |
|
|
z |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
z - |
2 |
|
|
|
|
|
|
|
|
|
2 |
1- |
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 nå=0è |
2 ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
¥ |
|
æ |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
ö |
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
кольце V1 |
|
f (z) = å |
ç1 |
- |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
÷z |
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||
|
|
|
2n+1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=0è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
- |
|
|
|
1 |
|
|
|
|
= - |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
= - |
1 |
|
|
¥ æ 1 |
|
ön |
= - |
-1 |
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
> 1), |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||
b) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç |
|
|
÷ |
|
|
|
|
|
z |
|
(сходится |
при |
|
|
z |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
z |
-1 |
|
|
|
|
|
|
|
|
|
|
|
æ |
|
|
|
|
|
|
|
1 ö |
|
|
|
|
|
|
z |
|
åè z |
ø |
|
|
|
|
|
å |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
zç1 - |
|
|
|
|
|
|
÷ |
|
|
|
|
|
|
|
|
n=0 |
|
|
|
|
|
|
n=-¥ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
поэтому |
|
|
|
в |
|
|
|
|
|
кольце |
|
|
|
|
|
|
|
V2 |
|
|
|
|
|
|
|
(с |
|
|
|
|
учетом |
|
|
второго |
разложения |
|
в |
|
|
a)) |
|||||||||||||||||||||||||||||||||||||||||||||||||
|
|
-1 |
|
|
|
n |
|
|
|
|
|
1 |
|
¥ |
|
æ z |
|
ön |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
f (z) = - å z |
|
|
- |
|
|
|
|
|
|
|
å |
ç |
|
|
|
|
÷ |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
n=-¥ |
|
|
|
|
|
|
|
|
2 n=0è |
|
2 |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
1 |
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
¥ |
|
|
æ |
2 ön |
|
|
1 |
-1 |
|
æ z |
ön |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
c) |
|
|
|
|
|
|
|
= |
|
|
|
× |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= |
|
|
|
|
|
|
åç |
|
|
|
÷ |
|
= |
|
|
|
å |
|
ç |
|
|
÷ |
|
(сходится при |
|
z |
> 2), поэтому в |
|||||||||||||||||||||||||||||||||
|
|
- |
|
|
|
|
|
|
|
æ |
|
|
|
|
|
2 |
ö |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
z |
2 |
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
n=0 |
è z |
ø |
|
|
|
|
|
2n=-¥ |
è 2 |
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ç1- |
|
|
|
÷ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
è |
|
|
|
|
|
ø |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
-1 |
|
æ |
|
1 |
|
ö |
|
n |
|
|
|
|
|
|||
кольце V3 (с учетом первого разложения в b)) |
|
|
f (z) = å |
ç |
|
|
|
|
-1÷z |
|
. |
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
n=-¥ |
è 2n+1 |
ø |
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
§5.4. Классификация изолированных особых точек |
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
однозначного характера |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
Точка z0 Î |
|
называется изолированной особой точкой функции |
f (z) , |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
C |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
если существует такая проколотая окрестность этой точки (т.е. |
0 < |
|
z - z0 |
|
|
< R |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
при конечной z0 |
|
|
|
|
или R < |
|
z |
|
< ¥ при z0 = ¥ ), в которой |
f (z) аналитична. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
В зависимости от поведения f (z) при приближении к такой точке различают три типа особых точек.
Изолированная особая точка z0 функции f (z) называется
а) устранимой точкой, если существует конечный предел lim f (z) = A;
z®z0
б) полюсом, если lim f (z) = ¥ ;
z®z0
в) существенно особой точкой, если lim f (z) не существует.
z®z0
Изолированные особые точки могут быть классифицированы по виду лорановского разложения функции в проколотой окрестности этой точки.
Теорема (критерий устранимой точки).
Изолированная |
особая точка z0 Î C функции |
f (z) является |
|||
устранимой тогда и |
только тогда, когда лорановское разложение |
f (z) |
в |
||
|
|
|
¥ |
|
|
окрестности точки z0 |
не содержит главной части, т.е. |
f (z) = åcn (z - z0 )n . |
|
||
|
|
|
n=0 |
|
|
Теорема (критерий полюса). |
|
|
|
|
|
Изолированная особая точка z0 Î C функции |
f (z) |
является полюсом |
|||
тогда и только тогда, когда главная часть лорановского разложения |
f (z) |
в |
|||
окрестности точки z0 содержит конечное число отличных от нуля членов,
|
|
|
|
¥ |
(z - z0 )n . |
|
|
|
|
|
|
т.е. f (z) = åcn |
|
|
|
|
|
||||||
|
|
|
n=-N |
|
|
|
|
|
|
||
Порядок полюса z0 |
функции f (z) |
равен кратности |
нуля функции |
||||||||
j(z) = |
|
1 |
|
в этой точке. |
Из теоремы |
о |
критерии |
полюса следует, что |
|||
f (z) |
|||||||||||
|
|
|
|
|
|
|
|
||||
порядок |
полюса |
совпадает |
с номером |
N |
старшего |
члена |
главной части |
||||
лорановского разложения функции в проколотой окрестности полюса.
Теорема (критерий существенно особой точки).
Изолированная особая точка z0 функции f (z) является существенно
особой тогда и только тогда, когда главная часть лорановского разложения функции f (z) в окрестности точки z0 содержит бесконечно много отличных
¥
от нуля членов, т.е. f (z) = åcn (z - z0 )n .
n=-¥
Эти критерии справедливы и для случая z0 = ¥ с учетом определения ряда Лорана в окрестности бесконечно удаленной точки.
Пример 5.5. Определить характер особых точек функций:
|
sin z |
|
1 |
1 |
|
||
|
|
|
|
|
|||
a) f (z) = |
; b) f (z) = |
; c) f (z) = e z . |
|||||
z |
(z - 2)n |
||||||
|
|
|
|
|
|||
Решение.
|
a) z = 0 – устранимая особая точка, так как lim |
sin z |
=1; |
|
|||||||||||||
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
z®0 |
z |
|
|
|
|
|||||
|
b) z = 2 – полюс порядка n , так как lim |
|
|
1 |
|
|
= ¥ , а порядок нуля |
||||||||||
|
|
|
|
|
|
|
|||||||||||
|
(z - |
2)n |
|||||||||||||||
|
|
|
|
|
|
z®2 |
|
|
|
|
|||||||
функции (z - 2)n в точке z = 2 равен n ; |
|
|
|
|
|
|
|
|
|
|
|||||||
|
c) z = 0 – существенно особая точка, так как при стремлении z = x к 0 |
||||||||||||||||
по действительной оси предел справа равен ¥ , |
а слева 0; при стремлении |
||||||||||||||||
|
1 |
|
|
1 |
|
|
|
|
|
1 |
|
|
|||||
|
|
|
|
|
|
|
|
|
|
вообще не имеет |
|||||||
z = iy |
к 0 по мнимой оси функция e z = cos |
- i sin |
|||||||||||||||
y |
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
y |
||||||
предела. |
|
|
|
|
|
|
|
|
|
|
|||||||
|
Пример 5.6. Найти полюсы функции f (z) и определить их кратности: |
||||||||||||||||
|
|
z ez |
1 |
|
|
|
|
|
|
|
|
||||||
a) |
f ( z )= |
|
; b) f (z)= |
|
|
. |
|
|
|
|
|||||||
z4 - z3 - 3z2 + 5z - 2 |
z3 (1 - cos z) |
|
|
|
|
||||||||||||
|
Решение. |
|
|
|
|
|
|
|
|
|
|
||||||
|
a) Запишем функцию f ( z ) в виде f ( z ) = |
|
|
|
z ez |
|
|
|
. |
||||||||
|
(z -1)3 (z + 2) |
||||||||||||||||
Точки z =1 и z = -2 являются полюсами, так как
|
lim |
|
z ez |
|
= ¥ , lim |
z ez |
|
|
= ¥ . |
||
|
|
|
|
(z -1)3 |
(z + 2) |
||||||
|
z ®1 (z -1)3 (z + 2) |
|
z ® -2 |
|
|||||||
Точки |
z = 1 и |
|
z = -2 нули знаменателя, причем |
z = 1– нуль третьего |
|||||||
порядка, а |
z = -2 |
простой нуль. |
Числитель в |
этих |
|
|
точках в нуль не |
||||
обращается, поэтому точки z = 1 и z = -2 будут соответственно полюсами 3-
го и 1-го порядка функции f ( z ) .
b) Нулями знаменателя будут точки z = 2p n, n Î Z . Разложим
знаменатель f (z) в ряд Тейлора в окрестности z = 0 :
