мк экзамен / шпоры металлы / 11

11. Устойчивость внецентренно сжатых э-тов.

При приложении сжимающей силы с эксцентриситетом стержень работает как внецентренно сжатый. При одновременном приложении продольной осевой силы и поперечной нагрузки, вызывающей изгиб, стержень будет сжато-изгибаемым. В целях упрощения практических методов расчета (в не­большой запас) сжато-изгибаемые стержни при рассмотрении критиче­ского состояния потери устойчивости приравниваются к внецентренно сжатым, имеющим эксцентриситет e=M/N.Даже при осевом приложении нагрузки всегда имеются случайные эксцентриситеты, и поэтому работа центрально сжатых стержней является по су­ществу работой сжатых стержней с малыми эксцентриситетами. Работа же внецентренно сжатых стержней с большими или малыми эксцентри­ситетами не имеет принципиальных отличий; только большие значения эксцентриситетов и моментов сказываются на работе внецентренно сжа­тых стоек более ярко, процесс же потери устойчивости остается тож­дественным.

При внецентренном сжатии с самого начала приложения нагрузки помимо продольной деформации возникает изгиб стержня (рис. 3.19,а).

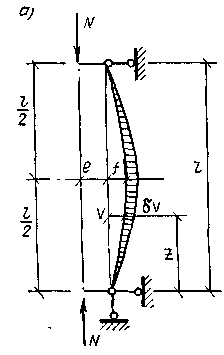
Рис3.19а — расчетная схема;

Поэтому расчет таких стержней следует проводить по деформированной схеме. На рис. 3.19,б показана зависимость между сжимающей силой N и стрелкой прогиба стержня v. Восходящая ветвь диаграммы характери­зует устойчивое состояние стержня, нисходящая — неустойчивое, а не­сущая способность равна максимальному значению сжимающей силы N_u, которая может быть воспринята стержнем.

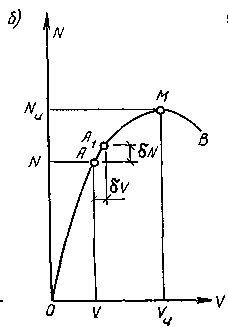
Рис3.19 б— кривая состояния равновесия,

При определении критической (предельной) силы N_u принимаются следующие основные предпосылки:

перемещения считаются достаточно малыми, что позволяет использо­вать приближенное выражение для кривизны изогнутой оси

(1)

относительные деформации в поперечном сечении е следуют гипоте­зе плоских сечений (рис. 3.19, в)

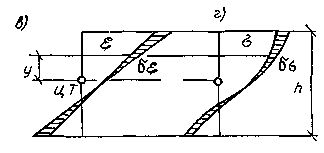
Рис3.19 в — эпюра деформаций в сече­нии; г — эпюра напряжений;

(2)

связь между нормальными напряжениями σ и относительными де­формациями ε для материала устанавливается зависимостью

(3)

в процессе возрастания нагрузки и в момент потери устойчивости влияние разгрузки не учитывается, т. е. Рассматривается нелинейно уп­ругий материал (см. рис. 3.16, в и 3.19,б) как в условиях догрузки, так и разгрузки. Для определения предельной нагрузки N_u применим метод бесконеч­но малых возмущений в окрестностях состояний равновесия стержня. Для этого рассмотрим некоторое исходное состояние равновесия в точ­ке А (см. рис. 3.19,б). Условия равновесия внешних и внутренних сил и изгибающих моментов в сечениях стержня имеют вид (4)

(5)

Наряду с этим рассмотрим другое состояние равновесия в точке А₁ отличающееся от исходного на бесконечно малую величину перемеще­ния δv (см. рис. 3.19, а, б). При этом деформации и напряжения в сече­ниях получают приращения, равные соответственно δε и δσ(см. рис. 3.19, в, г). Условия равновесия внешних и внутренних сил и моментов для нового равновесного состояния в точке A₁ получат следующий вид:

(6)

Вычитая почленно из уравнений (6) уравнения (5) с точностью до бесконечно малых второго порядка, получим условия равновесия для бесконечно малых приращений:

(7)

Полученные зависимости (7) справедливы для любой точки кри­вой состояний равновесия ОМВ (см. рис. 3.19,б). Практический интерес представляет решение этих уравнений для точки М максимума кривой ОМВ. В бесконечно малой окрестности точки М сжимающая сила постоянна, в связи, с чем имеем δN=0. При этом из уравнений (7) получаем:

(8)

Из диаграммы работы материала σ=f(ε) имеем (см. рис. 3.19,д)

(9)

где Е_t — касательный модуль для диаграммы работы материала стержня.

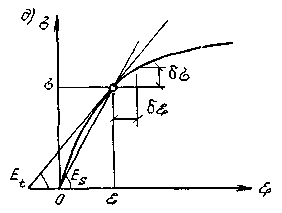
Рис3.19 д- диаграмма работы материала.

С учетом (2) находим

(10)

Подставляя δσ из (9) в условия равновесия (8) с учетом (10), получим:

(11) 'а

Определяя из первого уравнения системы (11) величину δε₀ и под­ставляя ее во второе уравнение этой системы, получим дифференциаль­ное уравнение для определения N_u в следующем виде:

(12)

где I_t — момент инерции приведенного с учетом касательного модуля сечения относи­тельно его собственной центральной оси. При решении практических задач форма изогнутой оси обычно при­нимается по полуволне синусоиды (см. рис. 3.19, а)

(13)

В этом случае условия равновесия до-статочно рассмотреть только в наиболее напряженном (срединном) сечении стержня. При этом из ре­шения уравнения (12) с учетом (13) находим

(14)

Для определения приведенной жесткости стержня El_t необходимо знать эпюру напряжений в наиболее нагруженном сечении стержня. Зависимость (3.45) можно записать в виде

σ = E_sε = E_s(ε₀-v"y), (15)_

где Е_s - секущий модуль (см. рис. 3.19,д).Тогда, рассматривая систему (4) с учетом (3) получим дифференциальное уравнение изгиба внецентренно сжатого стержня

(16)

где /_ef = М/Eρ— момент инерции приведенного с учетом секущего E_s модуля сечения относительно его собственной центральной оси. Из решения уравнения (16) с учетом (13) для срединного сечения стержня в точке максимума М кривой его состояний равновесия (v = f; N = N_u) получаем

(17)

Проверка устойчивости элементов постоянного сечения в плоскости действия момента, совпадающей с плоскостью симметрии (изгибная форма потери устойчивости), производится по формуле

. где φ_вн = σ_кр.вн/R — коэффициент снижения расчетных напряжений при внецентренном сжатии определяется в зависимости от условной гибкости

и приведенного эксцентриситета m₁, определяемого по формуле

m₁=ηm (18)

где η— коэффициент влияния формы сечения, m= eA/W_c—относительный эксцентриситет (отношение эксцентриситета к радиусу ядра сечения); W_c — момент сопротивле­ния для наиболее сжатого волокна, e = M/N - эксцентриситет приложения нормаль--ной силы, М — расчетный момент, принимаемый в зависимости от усло--вий закрепления стержня по концам и вида эпюры моментов

Коэффициент влияния формы сечения учитывает степень ослабления сечения при потере устойчивости пластическими деформациями. При сжатии двутаврового сечения с эксцентриситетом в плоскости стенки (рис. 3.21, а) текучесть быстро распространяется по толщине полки и се­чение превращается в тавровое. Резкое ослабление сечения в этом слу­чае учитывается коэффициентом η> 1. В случае незначительного ослаб­ления сечения пластическими деформациями (рис. 3.21, б) коэффициент η<1.

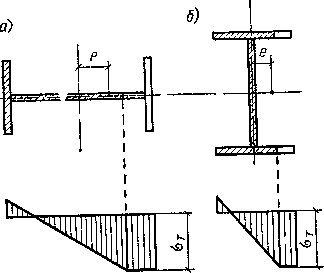
Рис. 3.21. Распространение пластических де­формаций в двутавровом сечении а — при эксцентриситете в плоскости стенки; б — при эксцентриситете перпендикулярно стенке.

Для прямоугольного сечения η= 1. В сквозных внецентренно сжатых стержнях напряжения по сечению ветвей распределяются почти равномерно, т.е. ветви работают на центральное сжатие. Поэтому расчет их на устойчивость ведут по появлению краевой текучести. Ко­эффициент влияния формы сечения в этом случае не учитывают. Если сжимающая сила приложена не в центре изгиба, то стержень не только изгибается, но и закручивается и теряет устойчивость по изгибно-крутильной форме. Переход части сечения в пластическую стадию работы смещает центр изгиба и также способствует закручиванию стержня. Эта форма потери устойчивости наиболее характерна для тон­костенных незамкнутых сечений, обладающих низкой крутильной жест­костью. Во внецентренно сжатых элементах, у которых жесткости в обоих главных направлениях различны (I_Х>I_У) и момент действует в плоско­сти наибольшей жесткости, возможна потеря устойчивости в плоскости, перпендикулярной действующему моменту. Проверка устойчивости та­ких стержней из плоскости действия момента производится по формуле

где φ_y — коэффициент продольного изгиба, принимаемый как для центрально сжатого стержня в зависимости от гибкости λ_у ; с — коэффициент, учитывающий изгибно-крутильную форму потери устойчивости и зависящий от относительного экс­центриситета и формы сечения.