Класический метод расчета переходных цепей

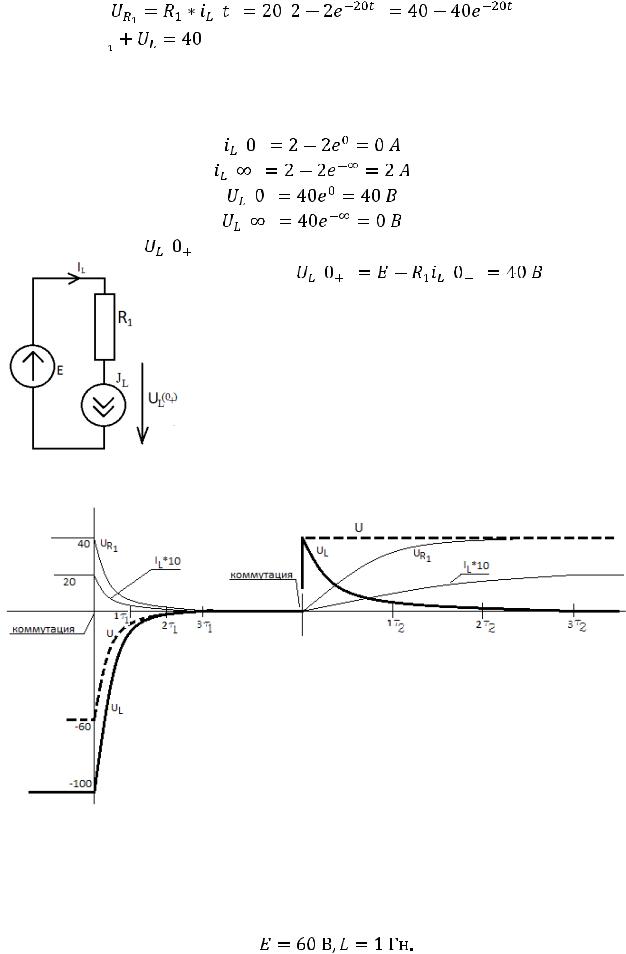
Тогда

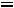
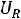
Проверить решение можно, подставляя в показатель степени экспоненты вместо t ноль или бесконечность:

1.6. Рассчитаем

, рис. 230:

Рис. 230

Графики:

Рис. 231

Пример 4. Найти токи и напряжения в схеме рис.232 с применением классического метода расчета при замыкании ключа.

Дано: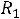

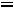
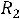
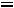
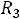
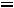
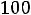
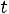
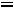
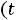
1.1. Составляем схему цепи до коммутации , заменяя индуктивность отрезком провода.

Расчет цепи в данном случае не требуется, потому что при разомкнутом ключе все токи и напряжения равны нулю.

Рис. 232

. Составляем схему цепи после коммутации

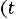
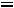
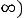– рис. 233:

Рис. 233

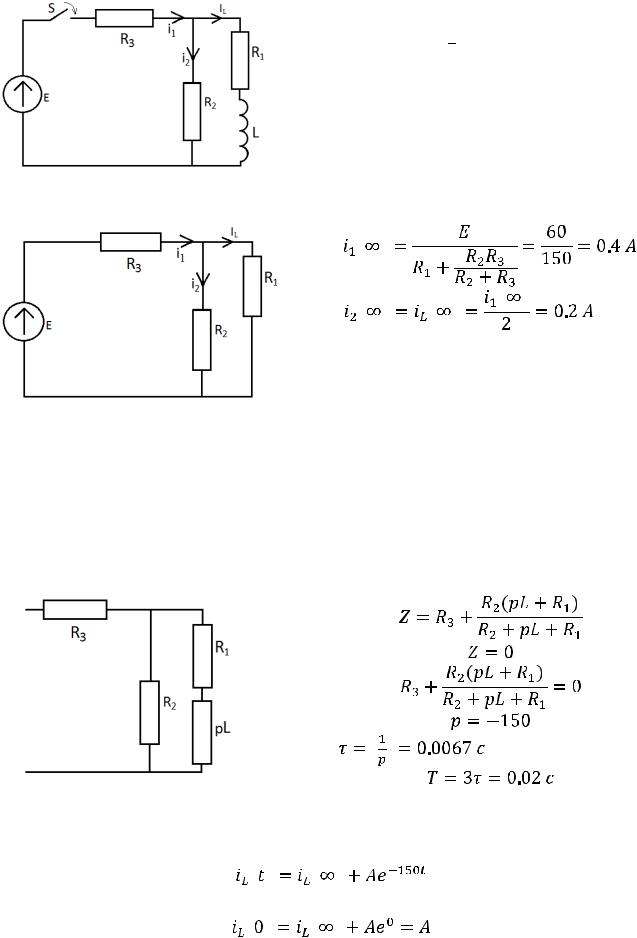
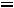
1.3. Составляем характеристическое уравнение и определяем его корни, которые будут показателями степени экспоненты. Исключаем источник энергии, заменяем индуктивность ее комплексным сопротивлением (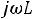), производим замену 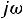на p. Получившаяся цепь представлена на рис. 234

Рис. 234

1.4. Теперь определим постоянную интегрирования. Запишем выражение для тока в индуктивности:

Запишем выражение для тока в момент времени 0:

Поскольку этот ток подчиняется закону коммутации, то

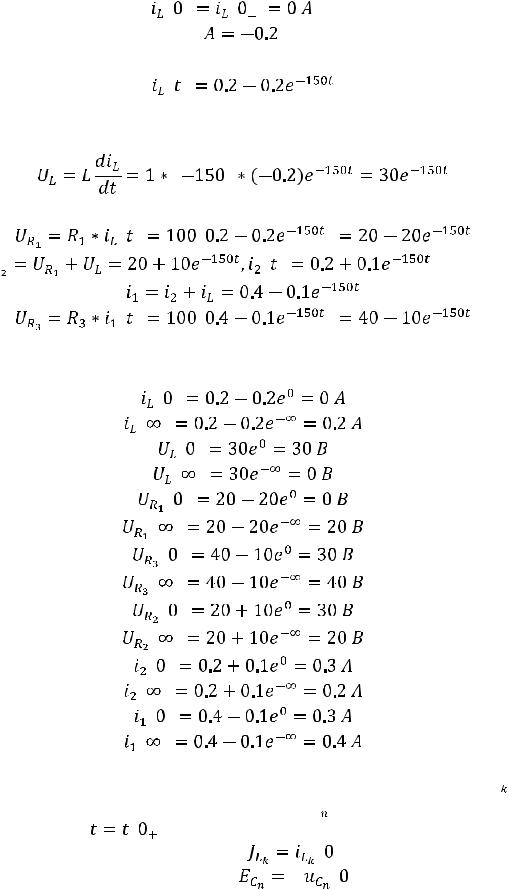
Таким образом, выражение для тока принимает вид:

1.5. Напряжение на индуктивности найдем, продифференцировав выражение для тока:

Можно также определить напряжение на резисторе :

Тогда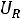

Проверить решение можно, подставляя в показатель степени экспоненты вместо t ноль или бесконечность:

1.6.Определить значения напряжений на индуктивных элементах и токов через ёмкостные элементы цепи 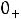непосредственно после

коммутации (	) можно,	заменив индуктивные элементы цепи
источниками тока со значениями							, а ёмкостные элементы –
источниками ЭДС со значениями								.Рассчитаем эту схему:

Рис. 235

Графики представлены ниже.

Решим тот же пример при размыкании ключа (рис. 236):

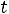
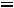
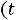
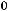
1.1.Составляем схему цепи до коммутации 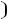. Рассчитаем цепь:

Рис. 236

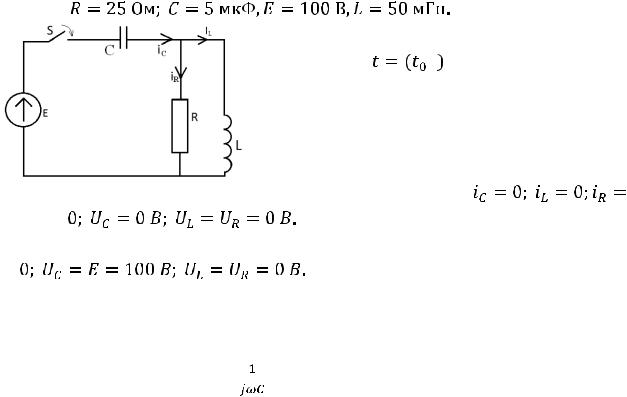
1.2.После размыкания ключа токи и напряжения в схеме нулевые: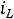

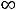
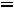
1.3.Рассчитаем комплексное сопротивление, составим характеристическое уравнение и определим его корни:

Рис. 237

1.4.Теперь определим постоянную интегрирования. Запишем выражение для тока:

Запишем выражение для тока в момент времени 0:

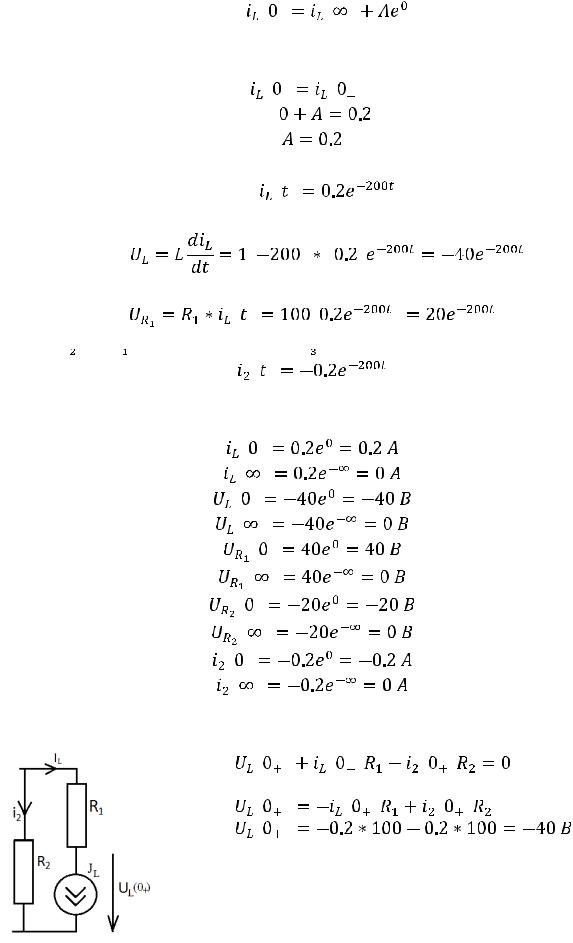
Поскольку этот ток подчиняется закону коммутации, то

Таким образом, выражение для тока принимает вид:

1.5.Определяем остальные величины:

Можно также определить напряжение на резисторе :

Тогда ; .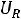

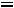
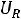
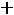
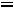
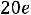
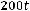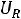
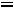
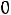Проверить решение можно, подставляя в показатель степени экспоненты вместо t ноль или бесконечность:

1.6.Рассчитаем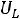

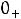
Рис. 238

Графики представлены на рис. рис. 240.

Цепи второго порядка (с двумя реактивными элементами).

Пример 5. Найти ток через индуктивность и напряжение на емкости в схеме рис. 239 с применением классического метода расчета при замыкании ключа.

Дано:
	1.1.	Составляем схему цепи до
	коммутации			, заменяя индуктивность
	отрезком провода, а емкость – разрывом
	цепи.
	Расчет цепи в данном случае не требуется,
	потому что при разомкнутом ключе все токи и
Рис. 239	напряжения равны нулю:

1.2.Составляем схему цепи после коммутации :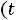

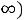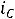
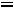
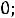
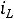
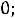
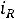
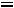
1.3.Составляем характеристическое уравнение и определяем его корни, которые будут показателями степени экспоненты. Исключаем источник энергии, заменяем индуктивность ее комплексным сопротивлением

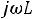(), а емкость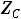 - производим замену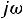 на p. Получившаяся цепь представлена на рис. 241.

Рис. 240 1.4. Теперь определим постоянные интегрирования. Запишем выражение

для тока в индуктивности и напряжения на емкости:

Запишем выражение для тока и напряжения в момент времени 0:

Рис. 241

Возьмем производные, тогда:

Тогда имеем систему:

Применим закон коммутации:

Заметим, что в последних двух уравнениях ток 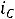равен:

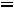
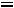
, поскольку в этот момент времени емкость можно

представить источником с нулевым значением ЭДС, а напряжение

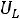
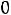
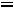
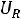
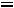
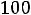
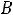, так как ток в индуктивности все еще сохраняет нулевое значение, индуктивность можно представить источником тока, сопротивление которого бесконечно, а ток равен нулю, и весь ток контура замыкается через резистор.

Таким образом, получили систему из четырех уравнений, которая позволяет найти все постоянные интегрирования:

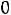
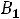
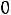
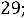
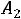
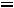
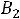
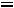
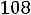
Запишем найденные ток и напряжение:

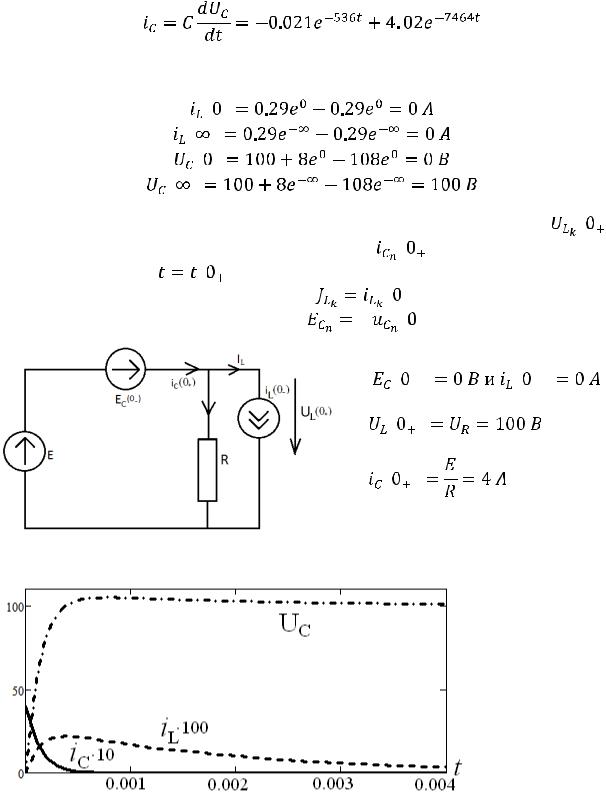
1.5. Ток в емкости определим, продифференцировав выражение для напряжения:

Проверить решение можно, подставляя в показатель степени экспоненты вместо t ноль или бесконечность:

1.6. Определить значения напряжений на индуктивных элементах			и
токов через ёмкостные элементы цепи		непосредственно после
коммутации (	) можно, заменив индуктивные элементы цепи

источниками тока со значениями						, а ёмкостные элементы –
источниками ЭДС со значениями							. Рассчитаем эту схему:
	Т.к.
	то

Рис. 242

Графики:

Рис. 242 а)

Пример 6. Найти ток	и напряжение	в схеме рис. 243 с
применением классического метода расчета при размыкании ключа.
Дано:
		1.1. Составляем схему цепи до
		коммутации		, заменяя

индуктивность отрезком провода, а

емкость – разрывом цепи (рис.

244). Расчет цепи в данном случае

проводим с тем, чтобы определить

ток в индуктивности и напряжение

Рис. 243

на емкости:

Рис. 244

1.2.Составляем схему цепи после коммутации – рис. 245:

Рис. 245

1.3. Составляем характеристическое уравнение и определяем его корни, которые будут показателями степени экспоненты. Исключаем источник энергии, заменяем индуктивность ее комплексным сопротивлением

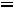
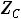
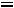
), а емкость – производим замену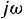 на p. Получившаяся цепь представлена на рис.246: