Класический метод расчета переходных цепей

Рис. 246

Корни комплексные:

1.4. Теперь определим постоянные интегрирования. Запишем выражение для тока в индуктивности и напряжения на емкости:

Запишем выражение для тока и напряжения в момент времени 0:

Возьмем производные, тогда:

Применим закон коммутации:

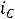
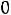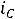
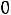
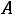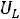
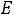
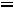
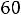
Заметим, что в последнем уравнении ток равен: , так как цепь в момент размыкания ключа кратковременно разрывается (емкость представляет собой разрыв), а напряжение 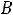, так как на резистивных элементах при нулевом токе падение напряжения равно нулю. Таким образом, получили систему из четырех уравнений, которая позволяет найти все постоянные интегрирования:

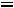
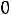
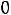
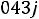
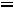
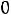
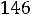
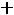
Запишем найденные ток и напряжение:

После упрощения этого выражения имеем:

1.5.Определим напряжение на емкости:

Упрощая, имеем:

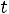
Пример 7. Определить токи и напряжения в цепи второго порядка (рис.247) операторным методом. Дано: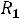

.

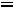
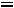
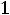
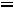
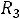
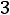
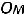
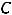
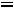
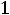
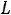
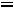
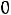
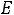
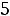
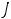
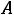Рис.247

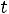
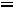
Переходный процесс в цепи вызван перераспределением энергии между реактивными элементами после коммутации ключа S (ключ закрывается). 1.1. Составляем схему цепи до коммутации , заменяя индуктивность отрезком провода, а емкость – разрывом цепи – рис. 248. При

разомкнутом ключе ток протекает лишь в ветви			, он равен току источника.
Этот ток создает падение напряжения на емкости			,
		.

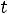
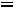
1.2.Составляем схему цепи после коммутации - рис. 249:

1.3.Составляем характеристическое уравнение и определяем его корни, которые будут показателями степени экспоненты. Исключаем источник

	энергии, заменяем
	индуктивность ее
	комплексным
	сопротивлением (				),
	а емкость			-
	производим замену				на p.
	Получившаяся цепь
	представлена на рис. 250.
Рис. 248	Здесь необходимо
	пересчитать звезду						в
	треугольник, произвести
	разрыв в ветви с емкостью,
	после чего приравнять

полученное сопротивление к нулю и найти корни. Полный расчет опущен, приведены только найденные корни.

Рис. 249

Рис. 250

1.4. Теперь определим постоянные интегрирования. Запишем выражение для тока в индуктивности и напряжения на емкости:

Запишем выражение для тока и напряжения в момент времени 0:

Возьмем производные, тогда:

Тогда имеем систему:

Применим закон коммутации:

Расчет тока 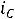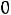и напряжения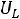 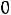представлен подробно в п. 1.6. Таким образом, получили систему из четырех уравнений, которая позволяет найти все постоянные интегрирования: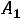

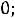
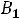
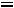
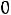
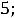
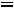
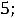
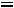
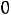
Запишем найденные ток и напряжение:

1.5. Ток в емкости определим, продифференцировав выражение для напряжения:

Проверить решение можно, подставляя в показатель степени экспоненты вместо t ноль или бесконечность:

1.6. Определить значения напряжений на индуктивных элементах								и
токов через ёмкостные элементы цепи							непосредственно после
коммутации (	) можно, заменив индуктивные элементы цепи
источниками тока со значениями						, а ёмкостные элементы –
источниками ЭДС со значениями							.Рассчитаем эту схему:

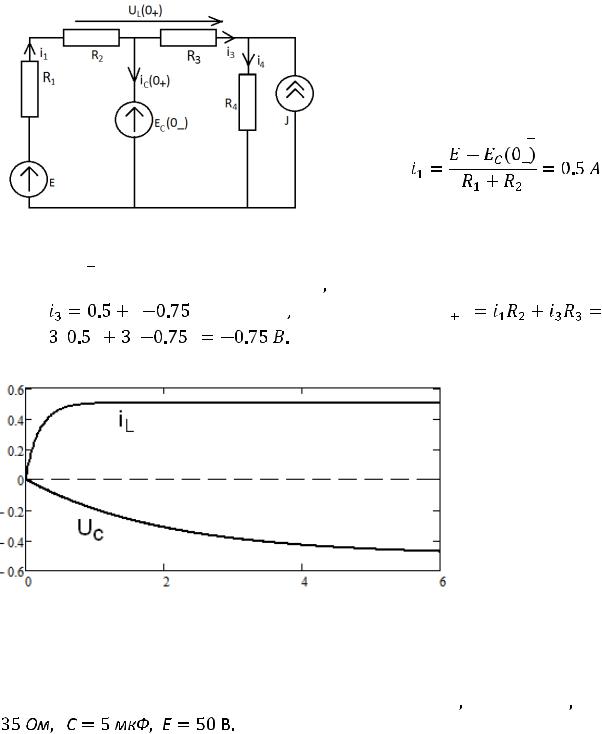
Из первого контура определим 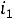ток . Ток 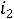равен току 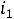, поскольку ток в индуктивности еще равен нулю в первый момент после коммутации.

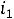
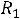
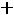
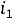
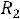
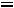
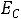
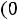
, откуда

Составим уравнение для второго Рис. 251 контура: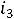

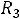
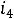
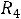
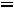
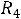
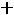
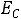
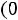
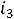
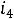
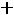
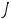
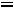
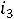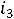
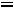
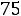
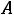
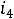
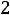
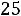
, с другой стороны, . Из этих двух уравнений находим токи и : . Тогда ток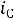

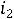
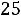
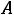а напряжение

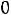
Графики:

Рис. 252

Пример 8.

Решить задачу классическим методом для схемы второго порядка на рис. 253 после размыкания ключа. Дано: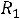

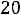
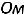
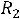
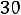
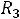
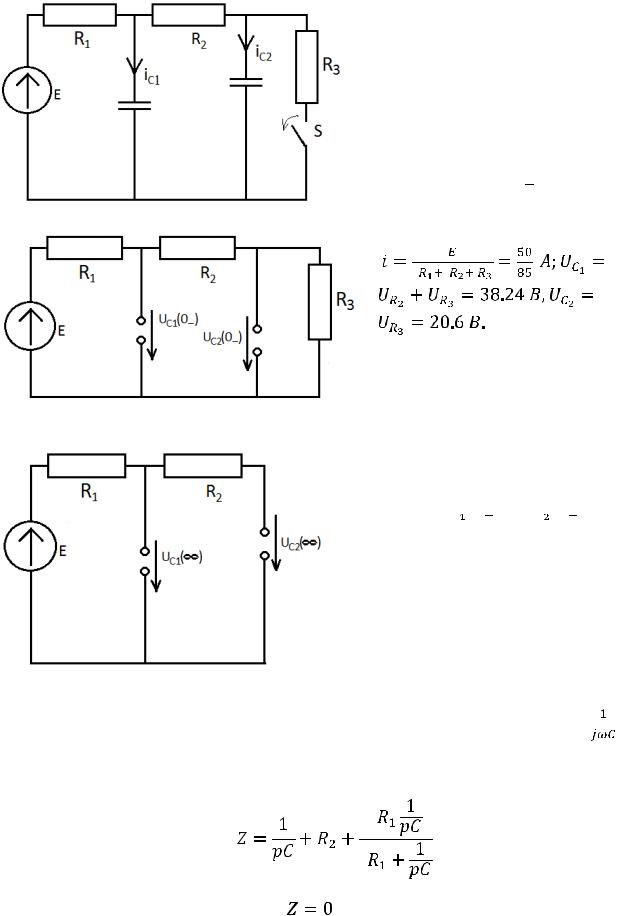
Рис. 253

Рис. 254

Переходный процесс в цепи вызван перераспределением энергии между реактивными элементами после коммутации ключа S (ключ размыкается).

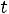
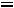
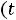
1.1. Составляем схему цепи до коммутации 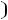, заменяя емкости разрывом цепи (рис.

254).

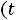
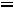
1.2. Составляем схему цепи после коммутации 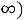– рис. 255: при разомкнутом ключе токи в цепи не

протекают. Падения напряжений на емкости

.

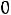
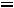
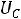
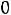
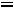
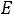
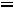
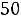
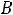1.3. Составляем характеристическое уравнение и определяем его корни, которые будут показателями степени

Рис. 255

экспоненты. Исключаем источник энергии, заменяем емкости комплексными сопротивлениями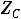

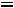
– производим замену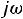 на p. Получившаяся цепь представлена на рис. 256:

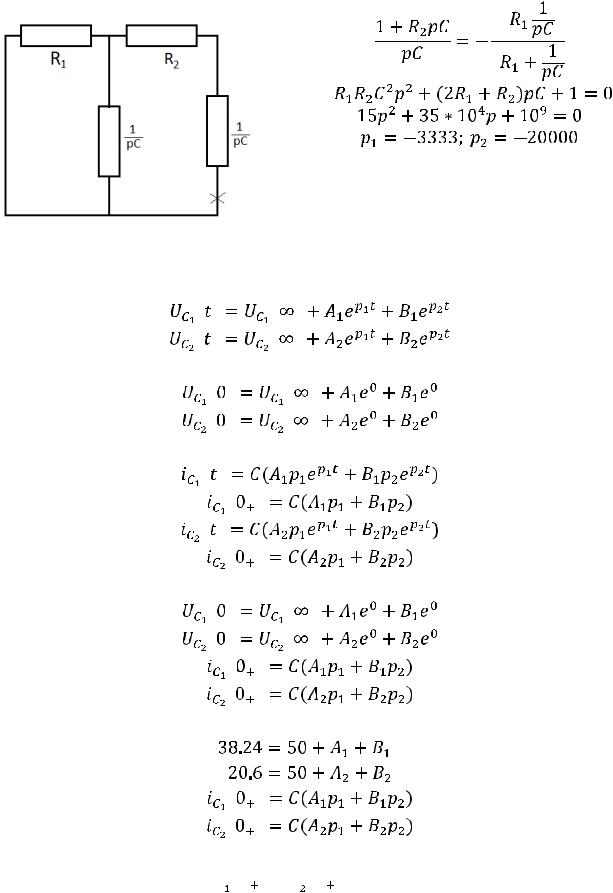
Рис. 256

1.4. Теперь определим постоянные интегрирования. Запишем выражение для тока в индуктивности и напряжения на емкости:

Запишем выражение для тока и напряжения в момент времени 0:

Возьмем производные, тогда:

Тогда имеем систему:

Применим закон коммутации:

Определим токи в емкостях в момент времени, непосредственно следующий за моментом коммутаци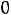и и 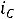. Их можно найти, проанализировав схему для момента коммутации (рис.257)

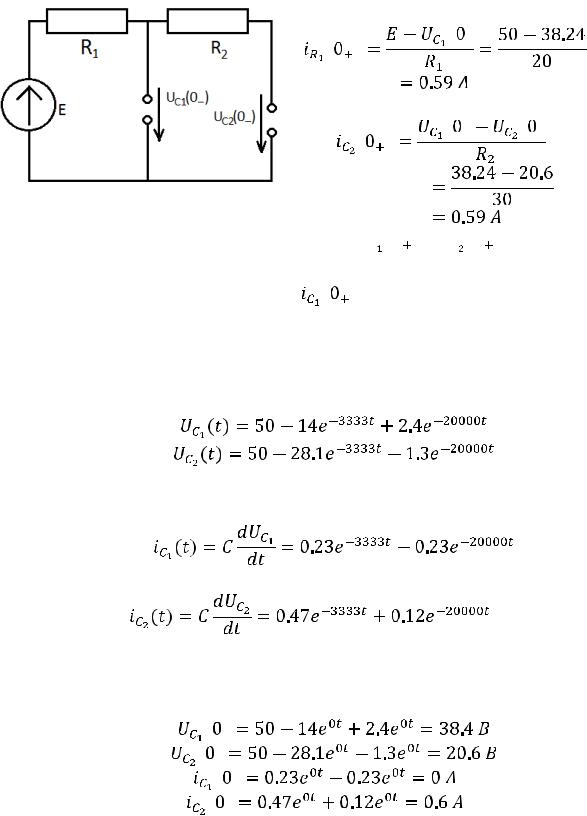
Из первого контура находим:

Из второго контура:

Рис. 257

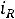
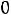
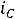
Так как , то по первому закону Кирхгофа

.

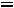
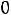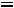
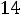
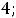
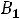
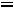
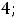
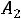
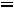
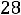
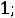
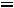
Таким образом, получили систему из четырех уравнений, которая позволяет найти все постоянные интегрирования: 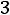. Запишем найденные напряжения:

1.5. Токи в емкостях определим, продифференцировав выражения для напряжений:

Проверить решение можно, подставляя в показатель степени экспоненты вместо t ноль или бесконечность:

Графики:

Рис. 258