МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РФ

ФГБОУ ВО Кемеровский технологический институт пищевой промышленности (университет)

Кафедра «Высшая математика»

Контрольная работа

по курсу «Методы оптимальных решений»

Студента _______________

Кемерово 2016

Вариант 5

1. Задания по теме "Нелинейное программирование"

Задание 1. Дана задача с нелинейной целевой функцией и линейной системой ограничений. Используя графический метод, найти глобальные экстремумы функции L=(x₁-3)²+(x₂-4)² при ограничениях:

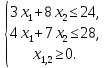
РЕШЕНИЕ. Область допустимых решений — OABD (рис. 1). Линиями уровня будут окружности с центром в точке O₁.

Рис. 1.

Максимальное значение целевая функция имеет в точке D (7, 0), минимальное — в точке A (0, 3). Поэтому L_max = (7-3)²+(0-4)² = 32; L_min=(0-3)²+(3-4)² = 10.

Ответ. Глобальный максимум, равный 32, достигается в точке D (7, 0), глобальный минимум, равный 10, — в точке A (0, 3).

Задание 2. Решить задачу дробно-линейного программирования. Для производства двух изделий A и В предприятие использует три типа технологического оборудования. Каждое из изделий должно пройти обработку на данном типе оборудования. Время обработки каждого из изделий, затраты, связанные с производством одного изделия, даны в таблице 1. Оборудование 1-го и 3-го типов предприятие может использовать не менее 48 и 8 ч соответственно, оборудование 2-го типа — не более 54 ч. Определить, сколько изделий следует изготовить предприятию, чтобы средняя себестоимость одного изделия была минимальной.

Таблица 1

Тип оборудования	Затраты времени на производство одного изделия, ч
	А	В
1	8	6
2	6	9
3	8	1
Затраты на производство одного изделия, тыс. р.	1	3

РЕШЕНИЕ. Составим математическую модель задачи. Пусть x₁ — количество изделий вида А, которое следует изготовить предприятию, x₂ — количество изделий вида В. Общие затраты на их производство составят (х₁ + 3x₂) тыс. р., а средняя себестоимость одного изделия будет равна (х₁ + 3x₂) /(х₁ + x₂).

Математическая модель задачи примет вид: L = (х₁ + 3x₂) / (х₁ + x₂) .

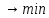при ограничениях:

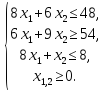
ΔАВС — область допустимых решений (рис. 2).

Рис. 2

Найдем x₂: L = (х₁ + 3x₂) / (х₁ + x₂), х₁ + 3x₂= Lх₁ + Lx₂, х₁ (1-L) = x₂(L-3),

х₁ = x₂(L-3)/(1-L) = k х₁. Угловой коэффициент прямой равен k = (L-3)/(1-L), тогда

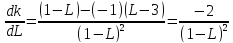
Так как dk/dL < 0, то функция k = (L - 2)/(3 - L) убывает. Это соответствует вращению прямой по часовой стрелке. Следовательно, в точке С (рис. 2) целевая функция будет иметь набольшее значение (глобальный максимум). Найдем координаты точки С. Решая систему

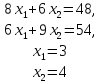
получим С (3, 4), 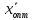= (3, 4), L = 15/7. Следовательно, предприятию следует выпускать 3 изделия вида А и 4 изделие вида В. При этом средняя себестоимость одного изделия будет минимальной и равной 2,14 тыс. р

Задание 3. Дана задача нелинейного программирования L = -х₁ x₂ при ограничении -х₁ + 3x₂ = 2. Найти условный экстремум с использованием метода множителей Лагранжа.

РЕШЕНИЕ. Составим функцию Лагранжа

F(x₁, x₂, λ₁) = -х₁ x₂ + λ₁(-х₁ + 3x₂ – 2)

Найдем частные производные функции Лагранжа по переменным x₁, x₂, λ₁. Приравняв к нулю полученные выражения, решим систему

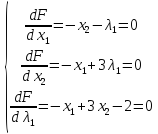
Откуда x₁ = -1, x₂ = 1/3, λ₁ = -1/3, L = 1/3. Определим характер экстремума, изменяя полученные значения переменных. Измененные значения должны удовлетворять заданной системе ограничений. Возьмем х₁ > -1, например x₁ = 0, тогда из системы ограничений получим х₂ = 2/3, L = 0. Возьмем х₁ < -1, например х1 = -2, тогда получим х₂ = 0, L = 0. Следовательно, L = 1/3 — максимальное значение функции.

Ответ. Точка экстремума x₁ = -1, x₂ = 1/3, при этом максимальное значение функции L = 1/3.